nLab fractional D-brane
Context
Cohomology
Special and general types
-
group cohomology, nonabelian group cohomology, Lie group cohomology
-
-
cohomology with constant coefficients / with a local system of coefficients
Special notions
Variants
-
differential cohomology
Extra structure
Operations
Theorems
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
For type II superstrings on a global orbifold spacetime , D-brane charge is measured by the equivariant K-theory (Witten 98, section 5.1) or at least some subgroup or quotient group thereof (BDHKMMS 01, around (137)). Under the canonical map from the plain topological K-theory of the quotient space irreducible elements of K-theory in general decompose into direct sums of smaller irreducible elements, hence into “smaller fractions stuck at the orbifold singularity” . The corresponding D-branes are called fractional D-branes in the literature.
In particular, at least for D-branes at an A-type singularity , hence for a cyclic group, the tension (hence mass) of a fractional D-brane is supposed to be the fraction of that of the unit bulk brane away from the singularity (Douglas-Greene-Morrison 97, p.10).
At global linear orbifold singularities
If here is a contractible space (at it is in the majority of examples discussed in the literature!), then its equivariant K-theory is equivalently that of the point
which is isomorphic to the representation ring of .
Under this identification, the (non-fractional) unit brane is identified with the regular representation of :
The non-fractional nature of the permutation representation is reflected in the fact that its character is still unity on the neutral element and vanishes on other elements (i.e. in the non-trivial twisted sectors):
But, by a standard fact from representation theory, the regular representation is far from irreducible, instead it is a direct sum of all existing irreducible representations (each appearing with multiplicity equal to its dimension):
In this sense, the unit brane on decays into fractional branes at the orbifold singularities .
For a general representation the general formula (see this Prop.)
shows that the total charge of the brane corresponding to , summed over all twisted sectors, is equal to the dimension of the fixed point space .
In terms of twisted sector boundary states
In the worldsheet-description of D-branes via boundary conformal field theory, fractional D-branes are reflected by boundary states in “twisted sectors”. (e.g. Diaconescu-Gomis 99, Recknagel-Schomerus 13, around p. 173)
D-branes on resolutions of orbifold singularities
In parts of the string theory literature, fractional D-branes are identified in a “dual” formulation of the situation:
At least for and a finite subgroup of SU(2) acting in the canonical way, hence for an ADE-singularity, the K-theoretic McKay correspondence (Gonzalez-Sprinberg & Verdier 83) identifies the equivariant K-theory of with the plain K-theory of a nice blow-up resolution :
Under this equivalence (isomorphism of K-theory groups), fractional D-branes on the orbifold are identified with D-branes on which are wrapped around some of the cycles in that appear through the blow-up of the ADE-singularity (in physics jargon these are the “vanishing cycles”).
In terms the worldvolume gauge theories
In terms of the worldvolume gauge field theory the equivalence (1) between
-
fractional D-branes stuck at orbifold singularities
-
and wrapped branes on the blow-up resolution
is supposed to be exhibited by passage from the Higgs branch to the Coulomb branch:
The first key insight is due to Kronheimer 89. He showed that the (resolutions of) the orbifold quotients for a finite subgroup of SU(2) are precisely the generic form of the gauge orbits of the direct product of -s acting in the evident way on the direct sum of -s, where and range over the vertices of the Dynkin diagram, and over its edges.
This becomes more illuminating when interpreted in terms of Yang-Mills gauge theory: in a “quiver gauge theory” the gauge group is a direct product group of circle group factors associated with vertices of a quiver, and the particles which are charged under this gauge group arrange, as a linear representation, into a direct sum of -s, for each edge of the quiver.
Pick one such particle, and follow it around as the gauge group transforms it. The space swept out is its gauge orbit, and Kronheimer says that if the quiver is a Dynkin diagram, then this gauge orbit looks like .
On the other extreme, gauge theories are of interest whose gauge group is not a big direct product, but is a simple Lie group, in the technical sense, such as the special unitary group or the exceptional Lie group . The mechanism that relates the two classes of examples is spontaneous symmetry breaking (“Higgsing”): the ground state energy of the field theory may happen to be achieved by putting the fields at any one point in a higher dimensional space of field configurations, acted on by the gauge group, and fixing any one such point “spontaneously” singles out the corresponding stabilizer subgroup.
Now here is the final ingredient: it is N=2 super Yang-Mills theories (“Seiberg-Witten theory”) which have a potential that is such that its vacua break a simple gauge group such as down to a Dynkin diagram quiver gauge theory. One place where this is reviewed, physics style, is Albertsson 03, section 2.3.4.
More precisely, these theories have two different kinds of vacua, those on the “Coulomb branch” and those on the “Higgs branch” depending on whether the scalars of the “vector multiplets” (the gauge field sector) or of the “hypermultiplet” (the matter field sector) vanish. The statement above is for the Higgs branch, but the Coulomb branch is supposed to behave “dually”. (see e.g. Diaconescu-Gomis 99)
So that then finally is the relation, in the ADE classification, between the simple Lie groups and the finite subgroups of SU(2): start with an N=2 super Yang-Mills theory with gauge group a simple Lie group. Let it spontaneously find its vacuum and consider the orbit space of the remaining spontaneously broken symmetry group. That is (a resolution of) the orbifold quotient of by a finite subgroup of SU(2).
Fractional M-branes
An analogous McKay correspondence for (fractional) M-branes
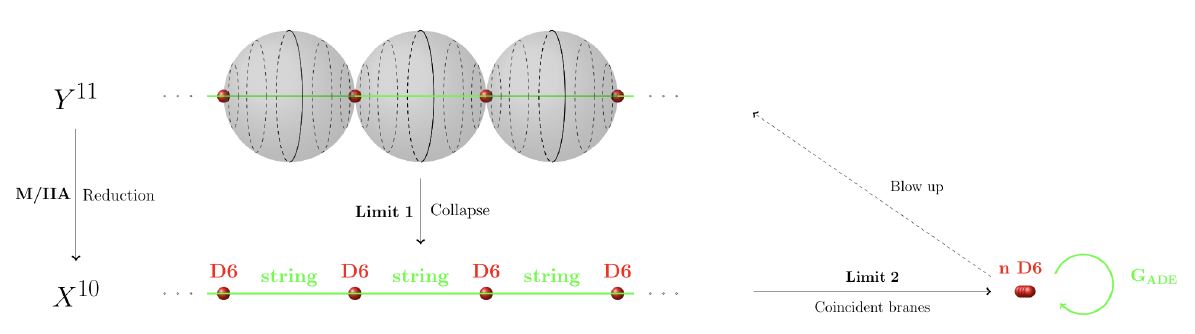
graphics grabbed from HSS18
is considered informally in the string theory literature (for instance in discussion of M-theory on G₂-manifolds) but has not been given a correspondingly precise cohomological formulation yet.
Properties
RR-Charge
Under the identification (above)
of the fractional D-brane charges at a -orbifold singularity with of the equivariant K-theory of the point and hence with the representation ring of , a character
of a representation correspondes to the RR-field charge
of the corresponding fractional D-brane in the -twisted sector.
(Douglas-Greene-Morrison 97, (3.8), Diaconescu-Gomis 99 (2.4), Billó-Craps-Roose 01, (4.65) with (4.41), EGJ 05, (4.5), Recknagel-Schomerus 13 (4.102))
Tadpole cancellation
See at RR-field tadpole cancellation the section For fractional D-branes
Related concepts
References
The concept originates with
-
Michael Douglas, Brian Greene, David Morrison, Orbifold Resolution by D-Branes, Nucl.Phys.B506:84-106,1997 (arXiv:hep-th/9704151)
-
Diaconescu, Michael Douglas, Jaume Gomis, Fractional Branes and Wrapped Branes, JHEP 9802:013,1998 (arXiv:hep-th/9712230)
based on the analysis of perturbative string theory on (global) orbifold backgrounds in
-
Lance Dixon, Jeff Harvey, Cumrun Vafa, Edward Witten, Strings on orbifolds, Nuclear Physics B Volume 261, 1985, Pages 678-686 (doi:10.1016/0550-3213(85)90593-0)
-
Lance Dixon, Jeff Harvey, Cumrun Vafa, Edward Witten, Strings on orbifolds (II), Nuclear Physics B Volume 274, Issue 2, 15 September 1986, Pages 285-314 (doi:10.1016/0550-3213(86)90287-7)
The proposal that D-brane charge on orbifolds is given by equivariant K-theory goes back to
- Edward Witten, section 5.1 of D-Branes And K-Theory, JHEP 9812:019,1998 (arXiv:hep-th/9810188)
but it was pointed out that only a subgroup or quotient group of equivariant K-theory can be physically relevant, in
- Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, around (137) of Triples, Fluxes, and Strings, Adv.Theor.Math.Phys. 4 (2002) 995-1186 (arXiv:hep-th/0103170)
Further discussion in terms of equivariant K-theory:
- Hugo Garcia-Compean, D-branes in Orbifold Singularities and Equivariant K-Theory, Nucl.Phys. B557 (1999) 480-504 (arXiv:hep-th/9812226)
Survey with an eye towards string phenomenology is in
- Dmitry Malyshev, Herman Verlinde, D-branes at Singularities and String Phenomenology, Nucl.Phys.Proc.Suppl.171:139-163, 2007 (arXiv:0711.2451)
The McKay correspondence as an integral transform (Fourier-Mukai transform) in (equivariant) K-theory, and hence in terms of fractional D-brane charge is due to
- Gérard Gonzalez-Sprinberg, Jean-Louis Verdier, Construction géométrique de la correspondance de McKay, Ann. Sci. ́École Norm. Sup.16 (1983) 409–449. (numdam)
Detailed mathematical discussion of fractional D-branes in their incarnation as Ext-groups of coherent sheaves is in
- S. Katz, Tony Pantev, Eric Sharpe, D-branes, orbifolds, and Ext groups, Nucl.Phys. B673 (2003) 263-300 (arXiv:hep-th/0212218)
and with relation to Bridgeland stability conditions in
- Dmitry Malyshev, Herman Verlinde, D-branes at Singularities and String Phenomenology, Nucl.Phys.Proc.Suppl.171:139-163, 2007 (arXiv:0711.2451)
Also on stability:
- Bogdan Stefanski, Dirichlet Branes on a Calabi-Yau Three-fold Orbifold, Nucl.Phys.B589:292-314, 2000 (arXiv:hep-th/0005153)
See also
-
David Berenstein, Richard Corrado, Jacques Distler, Aspects of ALE Matrix Models and Twisted Matrix Strings, Phys. Rev. D 58, 026005 (1998) (arXiv:hep-th/9712049)
-
Emil Martinec, Gregory Moore, bottom of p. 3 of On Decay of K-theory (arXiv:hep-th/0212059)
Discussion in terms of twisted sector boundary states in worldsheet boundary conformal field theory includes
-
Diaconescu, Jaume Gomis, Fractional Branes and Boundary States in Orbifold Theories, JHEP 0010 (2000) 001 (arXiv:hep-th/9906242)
-
Matthias Gaberdiel, Bogdan Stefanski, Dirichlet Branes on Orbifolds, Nucl.Phys.B578:58-84, 2000 (arXiv:hep-th/9910109)
-
M. Frau, A. Liccardo, R. Musto, The Geometry of Fractional Branes, Nucl.Phys. B602 (2001) 39-60 (arXiv:hep-th/0012035)
-
M. Billó, B. Craps, F. Roose, Orbifold boundary states from Cardy’s condition, JHEP 0101:038, 2001 (arXiv:hep-th/0011060)
-
N. Quiroz, Bogdan Stefanski, Dirichlet Branes on Orientifolds, Phys.Rev. D66 (2002) 026002 (arXiv:hep-th/0110041)
(for orientifolds of orbifolds)
-
Jaydeep Majumder, Subir Mukhopadhyay, Koushik Ray, Fractional Branes in Non-compact Type IIA Orientifolds, JHEP0611:008, 2006 (arXiv:hep-th/0602135)
-
Igor Kriz, Leopoldo A. Pando Zayas, Norma Quiroz, Comments on D-branes on Orbifolds and K-theory, Int.J.Mod.Phys.A23:933-974, 2008 (arXiv:hep-th/0703122)
-
Andreas Recknagel, Volker Schomerus, Boundary Conformal Field Theory and the Worldsheet Approach to D-branes, Cambridge 2013 (spire:1308990)
Relation to permutation branes:
- Bobby Ezhuthachan, Suresh Govindarajan, T. Jayaraman, A quantum McKay correspondence for fractional 2p-branes on LG orbifolds, JHEP 0508 (2005) 050 (arXiv:hep-th/0504164)
On polarization of fractional D-branes:
- Timothy J. Hollowood, S. Prem Kumar, World-sheet Instantons via the Myers Effect and Quiver Superpotentials, JHEP 0210:077, 2002 (arXiv:hep-th/0206051)
Last revised on July 18, 2024 at 11:48:16. See the history of this page for a list of all contributions to it.