nLab Hermitian form

Contents

Context

Linear algebra

Complex geometry

Definition
Properties

General properties
Relation to Kähler spaces
As Real modules

Related concepts
References

Definition

(Hermitian form and Hermitian space)

Let $V$ be a real vector space equipped with a complex structure $J\colon V \to V$ . Then a Hermitian form on $V$ is

a complex-valued real-bilinear form

$h \;\colon\; V \otimes V \longrightarrow \mathbb{C}$

such that this is symmetric sesquilinear, in that:

$h$ is complex-linear in the first argument;
$h(w,v) = \left(h(v,w) \right)^\ast$ for all $v,w \in V$

where $(-)^\ast$ denotes complex conjugation.

A Hermitian form is positive definite (often assumed by default) if for all $v \in V$

$h(v,v) \geq 0$
$h(v,v) = 0 \phantom{AA} \Leftrightarrow \phantom{AA} v = 0$ .

A complex vector space $(V,J)$ equipped with a (positive definite) Hermitian form $h$ is called a (positive definite) Hermitian space.

Remark

A positive-definite and complete Hermitian vector space is called a Hilbert space.

Properties

General properties

Proposition

(basic properties of Hermitian forms)

Let $((V,J),h)$ be a positive definite Hermitian space (def. ). Then:

the real part of the Hermitian form

$g(-,-) \;\coloneqq\; Re(h(-,-))$

is a Riemannian metric, hence a symmetric positive-definite real-bilinear form

$g \;\colon\; V \otimes V \to \mathbb{R}$
the imaginary part of the Hermitian form

$\omega(-,-) \;\coloneqq\; -Im(h(-,-))$

is a symplectic form, hence a non-degenerate skew-symmetric real-bilinear form

$\omega \;\colon\; V \wedge V \to \mathbb{R} \,.$

hence

h = g - i \omega \,.

The two components are related by

(1)

\omega(v,w) \;=\; g(J(v),w) \phantom{AAAAA} g(v,w) \;=\; \omega(v,J(v)) \,.

Finally

h(J(-),J(-)) = h(-,-)

and so the Riemannian metrics $g$ on $V$ appearing from (and fully determining) Hermitian forms $h$ via $h = g - i \omega$ are precisely those for which

(2)

g(J(-),J(-)) = g(-,-) \,.

These are called the Hermitian metrics.

(eg. Huybrechts 2004, Lem. 1.2.15)

Proof

The positive-definiteness of $g$ is immediate from that of $h$ . The symmetry of $g$ follows from the symmetric sesquilinearity of $h$ :

\begin{aligned} g(w,v) & \coloneqq Re(h(w,v)) \\ & = Re\left( h(v,w)^\ast\right) \\ & = Re(h(v,w)) \\ & = g(v,w) \,. \end{aligned}

That $h$ is invariant under $J$ follows from its sesquilinarity

\begin{aligned} h(J(v),J(w)) &= i h(v,J(w)) \\ & = i (h(J(w),v))^\ast \\ & = i (-i) (h(w,v))^\ast \\ & = h(v,w) \end{aligned}

and this immediately implies the corresponding invariance of $g$ and $\omega$ .

Analogously it follows that $\omega$ is skew symmetric:

\begin{aligned} \omega(w,v) & \coloneqq -Im(h(w,v)) \\ & = -Im\left( h(v,w)^\ast\right) \\ & = Im(h(v,w)) \\ & = - \omega(v,w) \,, \end{aligned}

and the relation between the two components:

\begin{aligned} \omega(v,w) & = - Im(h(v,w)) \\ & = Re(i h(v,w)) \\ & = Re(h(J(v),w)) \\ & = g(J(v),w) \end{aligned}

as well as

\begin{aligned} g(v,w) & = Re(h(v,w) \\ & = Im(i h(v,w)) \\ & = Im(h(J(v),w)) \\ & = Im(h(J^2(v),J(w))) \\ & = - Im(h(v,J(w))) \\ & = \omega(v,J(w)) \,. \end{aligned}

Saying the same again in other words:

Remark

(Hermitian forms via Hermitian metrics)
The decomposition of a Hermitian form into its real part and imaginary part is traditionally written with the symbols

\langle-\vert-\rangle \;=\; g(-,-) + \mathrm{i} \omega(-,-)

or similar, where

g(-,-) \;\coloneqq\; \Re \langle-\vert-\rangle \,,

\omega(-,-) \;\coloneqq\; \Im \langle-\vert-\rangle \,.

are real bilinear forms on the underlying real vector space.

In fact, the real part fully determines the imaginary part and hence the Hermitian form:

\begin{array}{l} \omega(-,-) & = \Im \langle-\vert-\rangle \\ & = \Re \big(-\mathrm{i} \langle-\vert-\rangle\big) \\ & = \Re \langle \mathrm{i} - \vert - \rangle \\ & = \Re \langle J(-) \vert - \rangle \\ & = g\big(J(-), -\big) \,, \end{array}

where in the last line we introduced the complex structure $J$ on the underlying real vector space which promotes it back to the original complex vector space.

Notice that the complex structure $J$ is an orthogonal map with respect to the inner product $g$ , equivalently $g$ is a Hermitian metric with respect to $J$ , in that

\begin{array}{l} g\big(J(-), J(-)\big) \\ \;=\; \Re \big\langle \mathrm{i}(-) \big\vert \mathrm{i}(-) \big\rangle \\ \;=\; \Re \big( -\mathrm{i} \cdot \mathrm{i} \langle - \vert - \rangle \big) \\ \;=\; \Re \langle - \vert - \rangle \\ \;=\; g(-,-) \,. \end{array}

Conversely, for a real vector space equipped with a complex structure $J$ and a Hermitian metric $g$ , in that $g\big(J(-), J(-)\big) \,=\, g(-,-,)$ , the formula

\langle-\vert-\rangle \;=\; g(-,-) + \mathrm{i} g\big(J(-), -\big)

defines a Hermitian form on the corresponding complex vector space:

The linearity in the second argument is clear. The antilinearity in the first argument follows by:

\begin{array}{l} g(\mathrm{i}-,-) + \mathrm{i} g\big(J(\mathrm{i}-), -\big) \\ \;=\; g\big(J(-),-\big) + \mathrm{i} g\big(J\circ J (-), - \big) \\ \;=\; g\big(J(-),-\big) - \mathrm{i} g\big(-, - \big) \\ \;=\; -\mathrm{i} \Big( g(-,-) + \mathrm{i} g\big( J(-), - \big) \Big) \,. \end{array}

and Hermiticity follows by:

\begin{array}{l} g(w,v) + \mathrm{i} g\big( J(w), v \big) \\ \;=\; g(w,v) + \mathrm{i} g\big( J \circ J(w), J(v) \big) \\ \;=\; g(w,v) - \mathrm{i} g\big( w, J(v) \big) \\ \;=\; g(v,w) - \mathrm{i} g\big( J(v), w\big) \,. \end{array}

Relation to Kähler spaces

Proposition

(relation between Kähler vector spaces and Hermitian spaces)

Given a real vector space $V$ with a linear complex structure $J$ , then the following are equivalent:

$\omega \in \wedge^2 V^\ast$ is a linear Kähler structure (def. );
$g \in V \otimes V \to \mathbb{R}$ is a Hermitian metric (2)

where $\omega$ and $g$ are related by (1)

\omega(v,w) \;=\; g(J(v),w) \phantom{AAAAA} g(v,w) \;=\; \omega(v,J(v)) \,.

As Real modules

While a non-degenerate inner product $(-\vert-)$ on a finite-dimensional real vector space $V$ is equivalently a linear isomorphism to its dual vector space

\array{ V &\overset{\sim}{\longrightarrow}& V^\ast &\overset{\sim}{\longrightarrow}& V \\ v &\mapsto& (v\vert-) &\mapsto& v }

the analogous statement for Hermitian complex inner products $\langle - \vert - \rangle$ fails, since the corresponding maps

(3)

\array{ H &\overset{\sim}{\longrightarrow}& H^\ast &\overset{\sim}{\longrightarrow}& H \\ \vert \psi \rangle &\mapsto& \langle \psi \vert &\mapsto& \vert \psi \rangle }

are now complex anti-linear and hence not morphisms in the category of complex vector spaces.

(What one does get is a complex-linear isomorphism to the anti-dual linear space, eg. Karoubi & Villamayor 1973, p. 58 (3 of 31); Karoubi 2010, §1.)

But one may absorb this anti-linearity into an ambient category so that Hermitian/unitary structure regarded internally to that category looks just like Euclidean/orthogonal structure. Since this uses basic structures known from Atiyah’s Real K-theory — with capital “R”, KR-theory — it is suggestive and convenient to refer to “Real” structures, as follows:

Definition

Write

(4)

Mod_{\mathbb{R}}^{\mathbf{B}\mathbb{Z}_2} \;\;\; \coloneqq \;\;\; Func\big( \mathbf{B}\mathbb{Z}_2 ,\, Mod_{\mathbb{R}} \big)

for the category of real vector spaces equipped with a linear involution (equivalently the functor category from the delooping groupoid of the cyclic group of order two to the category $Mod_{\mathbb{R}}$ of real vector spaces).

This becomes a monoidal category whose modoidal stucture $\otimes$ is the tensor product of the underlying vector spaces equipped with the tensor product of their involutions.

Example

(Real complex numbers) The complex numbers regarded as a real vector space equipped with its real-linear involution given by complex conjugation is an object of (4). Moreover, since complex-conjugation is actually an algebra homomorphism on the complex numbers, the usual product operation makes this a monoid object internal to (4), which we will refer to as the Real complex numbers:

(5)

\mathbb{Z}_2 \curvearrowright \mathbb{C} \;\in\; Mon\big( Mod_{\mathbb{R}}^{\mathbf{B}\mathbb{Z}_2} \big) \,.

Definition

(Real complex modules) We say that the category of module objects over the Real complex numbers (5) internal to (4) is the category of Real complex modules:

Mod_{ \mathbb{Z}_2 \curvearrowright \mathbb{C} } \;\;\;\; \equiv \;\;\;\; Mod_{ \mathbb{Z}_2 \curvearrowright \mathbb{C} } \big( Mod_{\mathbb{R}}^{\mathbf{B}\mathbb{Z}_2} \big) \,.

Lemma

The category of Real complex modules (Def. ) is equivalent, as a symmetric monoidal category, to the category of complex vector spaces equipped with anti-linear involutions:

Mod_{ \mathbb{Z}_2 \curvearrowright \mathbb{C} } \;\; \simeq \;\; \big( V \,\colon\, Mod_{\mathbb{C}} \big) \times \big( \sigma \,\colon\, V \xrightarrow{ \mathbb{C} antilinear } V \big)

Proof

By direct unwinding of the definitions, one finds that the module property enforces the anti-linearity of the involution:

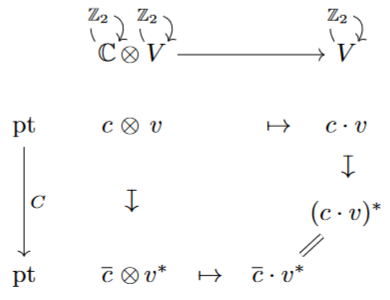
Moreover, to see that the tensor products agree one can argue that the relevant coequalizers (see here) in $Mod_{\mathbb{R}}^{\mathbf{B}\mathbb{Z}}$ are colimits in a category of presheaves which are computed objectwise — hence here over the single object of $\mathbf{B}\mathbb{Z}_2$ , where they agree with the usual tensor product of the underlying complex vector spaces.

The following construction is closely related to what is known as the hyperbolic functor with $\mathbb{Z}/2$ -equivariance, establishing an equivalence between KR-theory and topological Hermitian K-theory (see the references there):

Recall the equivalence of categories between real vector spaces and Real vector bundles over the point, given by complexification equipped with the involution by complex conjugation:

(6)

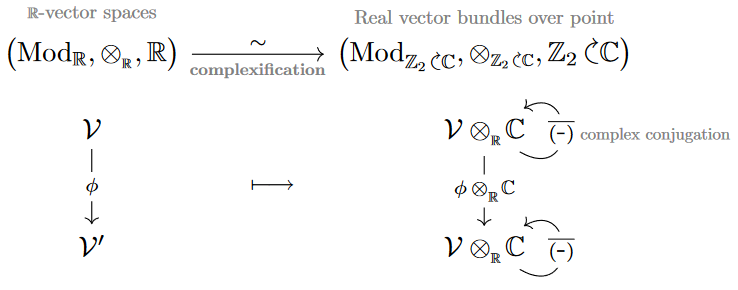
Proposition

(Hermitian forms are Real inner products)
Under the equivalence (6), a real inner product space $\mathscr{V} \,\in\, Mod_{\mathbb{R}}$ , $g \,\colon\, \mathscr{V} \otimes_{{}_{\mathbb{R}}} \mathscr{V} \to \mathbb{R}$ equipped with an isometric complex structure $J \,\colon\, \mathscr{V} \to \mathscr{V}$ , $g\big(J(-), J(-)\big) = g(-,-)$ is sent to corresponding Hermitian form $\langle -\vert-\rangle \,\equiv\, g(-,-) + \mathrm{i}g\big(J(-),-\big)$ , as follows:

(7)

Here

\mathscr{V}_{\pm J}

denotes the complex vector space whose underlying real vector space is

\mathscr{V}

and with complex structure

\pm J

Proof

On the right we used the following $\mathbb{Z}_2 \curvearrowright \mathbb{C}$ -module isomorphism from the plain complexification in (6):

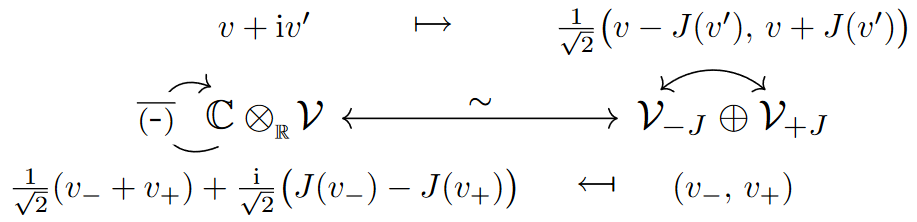
which serves to bring out the eigenspaces of $J \otimes_{{}_\mathbb{R}} \mathbb{C}$ :

(8)

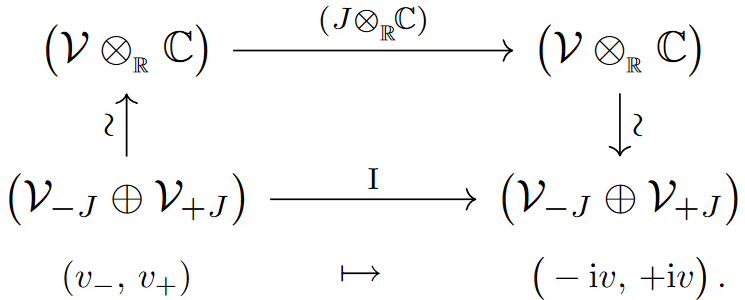
With this, the isometry condition $g \circ (J \otimes J) = g$ — which means that $g$ factors through the $(+1)$ -eigenspace of $J \!\otimes_{{}_\mathbb{R}}\! J$ — implies by functoriality of the equivalence (6) that the pairing on the right of (7) factors through the $(+1)$ -eigenspace of $\mathrm{I} \otimes \mathrm{I}$ (8), which already makes it a Hermitian form on $\mathscr{V}_{+J}$ , as shown on the right of (7). Explicit computation shows that this is indeed the one given by the traditional formula:

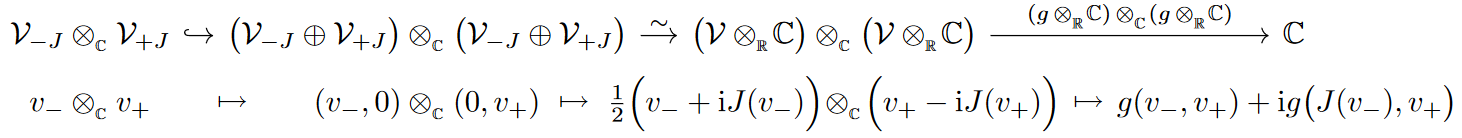
Example

(Complex Hermitian spaces as Euclidean Real complex modules)

For $H, \langle-\vert-\rangle_H$ a finite-dimensional complex Hermitian inner product space (assumed non-degenerate), its direct sum with its linear dual space carries the anti-linear involution induced (3) by the Hermitian form:

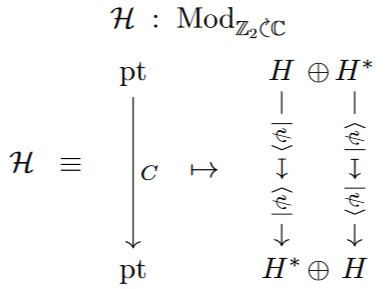
Therefore the Hermitian space $H$ induces a Real complex module by Lem. , which we denote by the corresponding script symbol:

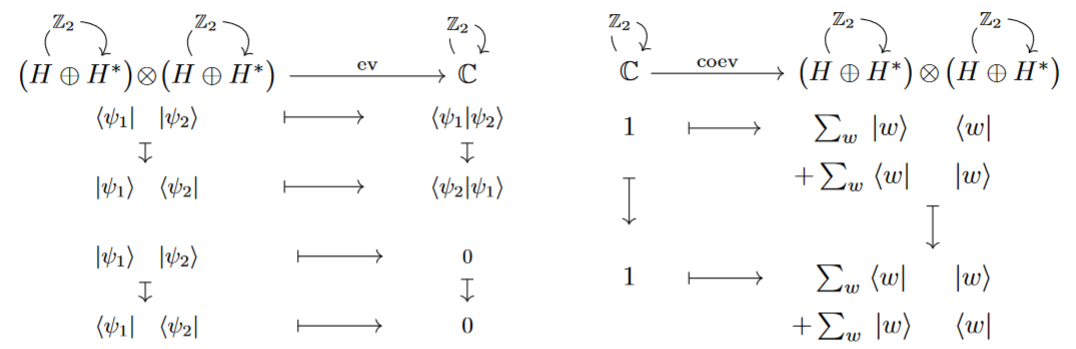
\mathscr{H} \;\coloneqq\; \mathbb{Z}_2 \curvearrowright \big( H \oplus H^\ast \big) \;\; \in \;\; Mod_{ \mathbb{Z}_2 \curvearrowright \mathbb{C} \,. }

Notice that the Real complex modules $\mathscr{H}$ arising this way have special properties:

$\mathscr{H}$ is a self-dual object, via the following (co-)evaluation maps

$\mathscr{H}$ carries an internal complex structure, namely an automorphism (now of Real complex modules!) which squares to minus the identity morphism:

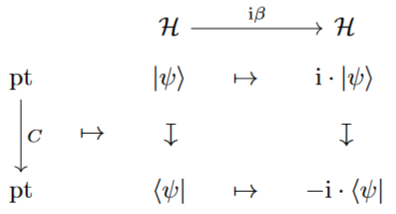
Due to this complex and self-dual structure we may think of $\mathscr{H}$ as being a Euclidean (instead of Hermitian) complex linear space but now internal to Real complex modules.

Proposition

Given a pair of (finite-dimensional, non-degenerate) complex Hermitian spaces $H, \langle-\vert-\rangle_H$ and $K, \langle-\vert-\rangle_K$ , there the complex linear maps between them are in bijection to the homomorphisms between the corresponding Real complex modules according to Exp. , as follows:

the ordinary $\mathrm{i}$ -complex linear maps $H \to K$ correspond to the $\mathrm{i}\beta$ -complex homomorphism $\mathscr{H} \to \mathscr{K}$
the ordinary unitary maps $H \to K$ correspond to the orthogonal maps $\mathscr{H} \to \mathscr{K}$ (namely those which respect the evaluation maps on these self-dual objects).

Proof

This follows by straightforward unwinding of the definitions:

First, for a homomorphism $\mathscr{H} \to \mathscr{K}$ to commute with $\mathrm{i}\beta$ its underlying complex linear map clearly needs to respect the direct sum, structure $H \oplus H^\ast \to K \oplus K^\ast$ , hence it needs to come from complex linear map $g \,\colon\,H \to K$ . But then the respect for the complex involution uniquely fixes the action $H^\ast \to K^\ast$ . Interestingly, it fixes them to be given by the linear dual of the operator adjoint $g^\dagger$ :

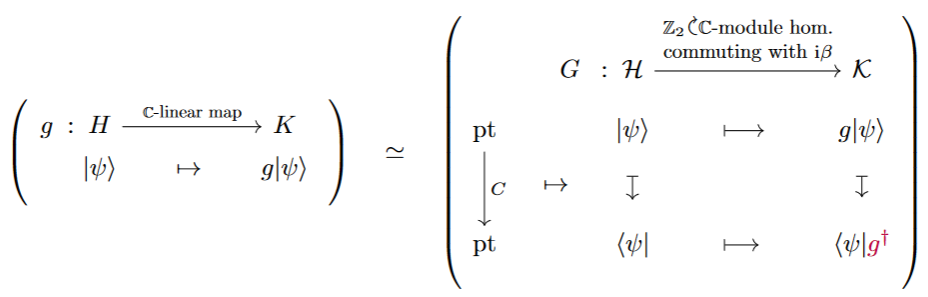
Second: A unitary map is a complex linear map that preserves the Hermitian form. But with the first point above one sees that this is equivalent to preserving the evaluation map on the corresponding Real complex modules:

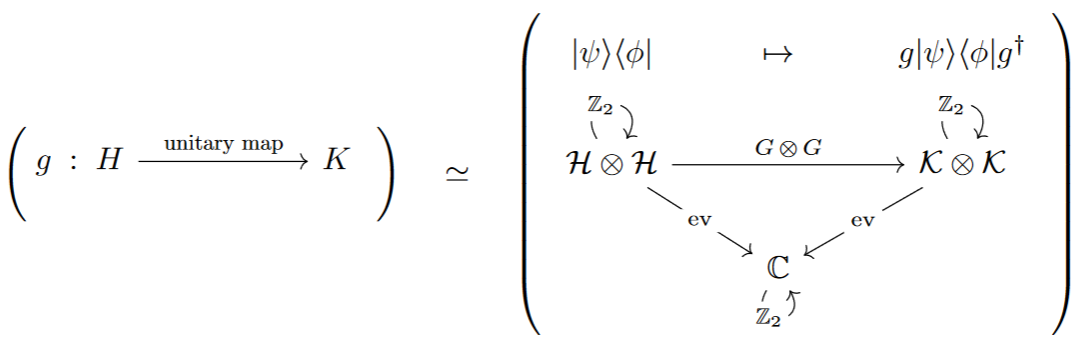
In summary: After internalization as Real complex modules, complex Hermitian/unitary space look like complex Euclidean/orthogonal spaces:

(…)

Related concepts

References

Hermitian forms are named in honor of the discussion of quadratic forms due to:

Charles Hermite, Sur la théorie des formes quadratiques. Premier mémoire, Journal für die reine und angewandte Mathematik 47 (1854) 313-342 [doi:10.1515/crll.1854.47.343]

maybe starting with

Luigi Bianchi, Forme definite di Hermite, §24 in: Sui gruppi di sostituzioni lineari con coefficienti appartenenti a corpi quadratici immaginarî, Mathematische Annalen 40 (1892) 332–412 [doi:10.1007/BF01443558]

see:

Jürgen Elstrodt, Fritz Grunewald, Jens Mennicke: Integral Binary Hermitian Forms, Ch. 9 in Groups Acting on Hyperbolic Space, Springer (1998) [doi:10.1007/978-3-662-03626-6_9]

Discussion of Hermitian forms over the complex numbers, as understood today, originates in the definition of Hilbert spaces (in laying of mathematical foundations of quantum mechanics):

John von Neumann, p. 64 in: Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren, Math. Ann. 102 (1930) 49–131 [doi:10.1007/BF01782338]
John von Neumann:

p. 21 in: Mathematische Grundlagen der Quantenmechanik, Springer (1932, 1971) [doi:10.1007/978-3-642-96048-2]

pp. 38 in: Mathematical Foundations of Quantum Mechanics Princeton University Press (1955) [doi:10.1515/9781400889921, Wikipedia entry]

Textbook account:

Nicolas Bourbaki, §V.1.1 in: Topological Vector Spaces, Chapters 1–5, Masson (1981), Springer (2003) [doi:10.1007/978-3-642-61715-7]
Daniel Huybrechts, §1.2 in: Complex geometry: An introduction, Universitext, Springer (2004) [doi:10.1007/b137952, pdf]

Textbook accounts in the context of operator algebras:

Richard V. Kadison, John R. Ringrose, §2.1 in: Fundamentals of the theory of operator algebras Vol I Elementary Theory, Graduate Studies in Mathematics 15, AMS (1997) [ISBN:978-0-8218-0819-1]
Bruce Blackadar, §I.1.1 in: Operator Algebras – Theory of $C^\ast$ -Algebras and von Neumann Algebras, Encyclopaedia of Mathematical Sciences 122, Springer (2006) [doi:10.1007/3-540-28517-2]
Klaas Landsman, §A.1 in: Foundations of quantum theory – From classical concepts to Operator algebras, Springer Open (2017) [doi:10.1007/978-3-319-51777-3, pdf]