nLab Shum's theorem
Context
Knot theory
Examples/classes:
Types
Related concepts:
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Contents
Statement
Proposition
(Shum's theorem)
The category of framed oriented tangles is equivalently the free ribbon category generated by a single object.
The following table indicates how the main axioms for ribbon categories translate to the corresponding moves on (framed, oriented) tangle/link diagrams (cf. e.g. Selinger 2011, Baez & Stay 2011), namely to isotopy moves and Reidemeister moves:
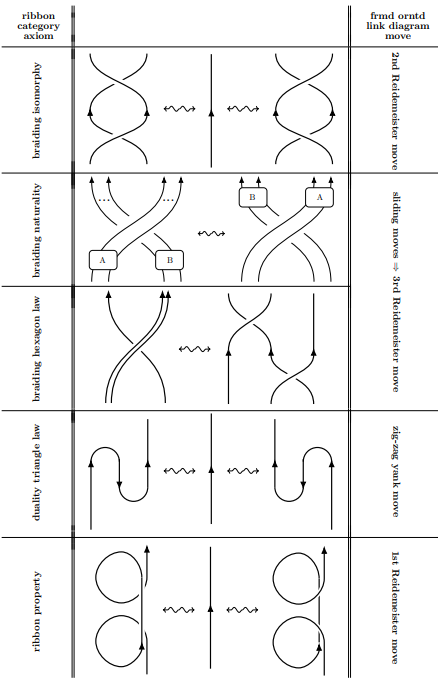
(NB: For the sliding moves, the corresponding mirrored moves are not shown, to save space.)
Relation to knot invariants
This means that for any ribbon category and any object, there is a unique ribbon functor
which sends the generating object to .
Since the endomorphisms of the object are the oriented framed links this means that the functor (1) restricts on endomorphisms to a collection of link invariants (with values in the endomorphism ring of whenever is Ab-enriched).
The standard link invariants arise this way (e.g. the HOMFLY polynomial), with the ribbon category being the category of representations (finite dimensional) of a quantum group (cf. Yetter 2001 p 118).
References
-
Mei Chee Shum, Tortile tensor categories, Journal of Pure and Applied Algebra 93 1 (1994) 57-110 [10.1016/0022-4049(92)00039-T]
-
David N. Yetter: Functorial Knot Theory – Categories of Tangles, Coherence, Categorical Deformations, and Topological Invariants, Series on Knots and Everything 26, World Scientific (2001) [doi:10.1142/4542]
Last revised on September 1, 2024 at 10:50:49. See the history of this page for a list of all contributions to it.