nLab geometry of physics - cohesive toposes
Gros toposes
We have seen roughly two different kinds of sheaf toposes:
-
categories of sheaves on a given space (Example ), which, by localic reflection (Prop. ), really are just a reflection of the space in the category of toposes,
these are called petit toposes;
-
categories of sheaves whose objects are generalized spaces (Example )
these are called gros toposes.
Remark
(cohesive generalized spaces as foundations of geometry)
If we aim to lay foundations for geometry, then we are interested in isolating those kinds of generalized spaces which have foundational a priori meaning, independent of an otherwise pre-configured notion of space. Hence we would like to first characterize suitable gros toposes, extract concepts of space from these, and only then, possibly, consider the petit topos-reflections of these (Prop. below).
The gros toposes of such foundational generalized spaces ought to have an internal logic that knows about modalities of geometry such as discreteness or concreteness. Via the formalization of modalities in Def. this leads to the definiton of cohesive toposes (Def. , Prop. below, due to Lawvere 91, Lawvere 07).
| gros topos | generalized spaces obey… | example: | |
|---|---|---|---|
| cohesion | Def. | principles of differential topology | SmoothSet |
| elasticity | Def. | principles of differential geometry | FormallSmoothset |
| solidity | Def. | principles of supergeometry | SuperFormalSmoothSet |
Cohesive toposes
Definition
A sheaf topos (Def. ) is called a cohesive topos if there is a quadruple (Remark ) of adjoint functors (Def. ) to the category of sets (Example )
such that:
-
and are full and faithful functors (Def. )
Example
(adjoint quadruple of presheaves over site with finite products)
Let be a small category (Def. ) with finite products (hence with a terminal object and for any two objects their Cartesian product ).
Then there is an adjoint quadruple (Remark ) of functors between the category of presheaves over (Example ), and the category of sets (Example )
such that:
-
the functor sends a presheaf to its set of global sections, which here is its value on the terminal object:
(3) -
and are full and faithful functors (Def. ).
-
preserves finite products:
for , we have a natural bijection
Hence the category of presheaves over a small category with finite products, hence the category of sheaves for the trivial coverage (Example ) is a cohesive topos (Def. ).
Proof
The existence of the terminal object in means equivalently (by Example ) that there is an adjoint pair of functors between and the terminal category (Example ):
whose right adjoint takes the unique object of the terminal category to that terminal object.
From this it follows, by Example , that Kan extension produces an adjoint quadruple (Remark ) of functors between the category of presheaves and , as shown, where
-
is the operation of pre-composition with the terminal object inclusion
-
is the left Kan extension along the inclusion of the terminal object.
The former is manifestly the operation of evaluating on the terminal object. Moreover, since the terminal object inclusion is manifestly a fully faithful functor (Def. ), it follows that also its left Kan extension is fully faithful (Prop. ). This implies that also is fully faithful, by (Prop. ).
Equivalently, is the constant diagram-assigning functor. By uniqueness of adjoints (Prop. ) implies that is the functor that sends a presheaf, regarded as a functor , to its colimit
The fact that this indeed preserves products follows from the assumption that has finite products, since categories with finite products are cosifted (Prop. )
Example suggests to ask for coverages on categories with finite products which are such that the adjoint quadruple (2) on the category of presheaves (co-)restricts to the corresponding category of sheaves. The following Definition states a sufficient condition for this to be the case:
Definition
We call a site (Def. ) cohesive if the following conditions are satisfied:
-
The category has finite products (as in Example ).
-
For every covering family in the given coverage on the induced Cech groupoid (Def. ) satisfies the following two conditions:
-
the set of connected components of the groupoid obtained as the colimit over the Cech groupoid is the singleton:
-
the set of connected components of the groupoid obtained as the limit of the Cech groupoid is equivalent to the set of points of , regarded as a groupoid:
-
This definition is designed to make the following true:
Proposition
(category of sheaves on a cohesive site is a cohesive topos)
Let be a cohesive site (Def. ). Then the adjoint quadruple on the category of presheaves over , from Example (given that a cohesive site by definition has finite products) (co-)restricts from the category of presheaves over , to the category of sheaves (Def. ) and hence exhibits as a cohesive topos (Def. ):
Proof
By example we alreaday have the analogous statement for the categories of presheaves. Hence it is sufficient to show that the functors and from Example factor through the definition inclusion of the category of sheaves, hence that for each set the presheaves and are indeed sheaves (Def. ).
By the formulaton of the sheaf condition via the Cech groupoid (Prop. ), and using the adjunction hom-isomorphisms (here) this is readily seen to be equivalent to the two further conditions on a cohesive site (Def. ):
Let be a covering family.
The sheaf condition (?) for says that
is an isomorphism of groupoids, which by adjunction and using (4) means equivalently that
is an isomorphism of groupoids, where we used that colimits of representables are singletons (Lemma ) to replace .
But now in this internal hom of groupoids, the set is really a groupoid in the image of the reflective embedding of sets into groupoids, whose left adjoint is the connected components-functor (Example ). Hence by another adjunction isomoprhism this is equivalent to
being an isomorphism (a bijection of sets, now). This is true for all precisely if (by the Yoneda lemma, if you wish) the morphism
is already an isomorphism (here: bijection) itself.
Similarly, the sheaf condition (?) for says that
is an isomorphism, and hence by adjunction and using (3), this is equivalent to
being an isomorphism. This holds for all if (by the Yoneda lemma, if you wish)
is an isomorphism.
Definition
(adjoint triple of adjoint modal operators on cohesive topos)
Given a cohesive topos (Def. ), its adjoint quadruple (Remark ) of functors to and from Set
induce, by composition of functors, an adjoint triple (Remark ) of adjoint modalities (Def. ):
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. ).
We pronounce these as follows:
| shape modality | flat modality | sharp modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a discrete object;
-
is called a codiscrete object;
-
is a concrete object.
Proposition
(pieces have points discrete objects are concrete Aufhebung of bottom adjoint modality)
Let be a cohesive topos (Def. ). Then the following conditions are equivalent:
-
pieces have points: For every object , comparison of extremes-transformation (?) for the -adjoint modality (?), hence the -counit of an adjunction composed with the ʃ-unit
is an epimorphism (Def. )
-
discrete objects are concrete: For every object , we have that its discrete object is a concrete object (Def. ).
-
Aufhebung of bottom adjoint modality
The adjoint modality exhibits Aufhebung (Def. ) of the bottom adjoint modality (Example ), i.e. the initial object (Def. ) is codiscrete (Def. ):
Proof
The comparison morphism is a special case of that discussed in Prop. . First observe, in the notation there, that
In one direction, assume that is an epimorphism. By (?) we have , but is a left adjoint and left adjoints preserve monomorphisms (Prop. ).
In the other direction, assume that is an epimorphism. By (?) and (?) we see that is re-obtained from this by applying and then composition with isomorphisms. But is again a left adjoint, and hence preserves epimorphism by Prop. , as does composition with isomorphisms.
By applying (?) again, we find in particular that pieces have points is also equivalent to being an epimorphism, for all . But this is equivalent to
being a monomorphism for all (by adjunction isomorphism (?) and definition of epimorphism, Def. ).
Now by Lemma , this is equivalent to
being an injection for all , which, by Def. , is equivalent to being a monomorphism, hence to discrete objects are concrete.
This establishes the equivalence between the first two items.
Proposition
(cohesive site such that pieces have points/discrete objects are concrete)
Let be a cohesive site (Def. ), such that
- for every object , there is at least one morphism from the terminal object to , hence such that the hom set is non-empty.
Then the cohesive topos , according to Prop. , satisfies the equivalent conditions from Prop. :
Proof
By Prop. it is sufficient to show the second condition, hence to check that for each set , the canonical morphism
is a monomorphism. By Prop. this means equivalently that for each object in the site, the component function
is an injective function.
Now, by the proof of Prop. , this is the diagonal function
This function is injective precisely if is non-empty, which is true by assumption.
Proposition
(quasitopos of concrete objects in a cohesive topos)
For a cohesive topos (Def. ), write
for its full subcategory (Example ) of concrete objects (Def. ).
Then there is a sequence of reflective subcategory-inclusions (Def. ) that factor the -adjunction as
If in addition discrete objects are concrete (Prop. ), then the full adjoint quadruple factors through the concrete objects:
Proof
For the adjunction on the right, we just need to observe that for every set , the codiscrete object is concrete, which is immediate by idempotency of (Prop. ) and the fact that every isomorphism is also a monomorphism. Similarly, the assumption that discrete objects are concrete says exactly that also factors through .
For the adjunction on the left we claim that the left adjoint , (to be called concretification), is given by sending each object to the image (Def. ) of its adjunction unit :
hence to the object which exhibits the epi/mono-factorization (Prop. ) of
First we need to show that , thus defined, is indeed concrete, hence that is a monomorphism (Def. ). For this, consider the following naturality square (?) of the -adjunction hom-isomorphism
By chasing the identity morphism on through this diagram, as shown by the diagram on the right, we obtain the equality displayed in the bottom right entry, where we used the general formula for adjuncts (Prop. ) and the definition (Def. ).
But observe that , and hence also , is an isomorphism (Def. ), as indicated above: Since is both a left adjoint as well as a right adjoint, it preserves both epimorphisms as well as monomorphisms (Prop. ), hence it preserves image factorizations (Prop. ). This implies that is the epimorphism onto the image of . But by idempotency of , the latter is an isomorphism, and hence so is the epimorphism in its image factorization.
Therefore the equality in (8) says that
where in the second line we remembered that is, by definition, the epimorphism in the epi/mono-factorization of .
Now the defining property of epimorphisms (Def. ) allows to cancel this commmon factor on both sides, which yields
This shows that is indeed concret.
It remains to show that this construction is left adjoint to the inclusion. We claim that the adjunction unit (Def. ) of is provided by (7).
To see this, first notice that, since the epi/mono-factorization (Prop. ) is orthogonal and hence functorial, we have commuting diagrams of the form
Now to demonstrate the adjunction it is sufficient, by Prop. , to show that is a universal morphism in the sense of Def. . Hence consider any morphism with . Then we need to show that there is a unique diagonal morphism as below, that makes the following top left triangle commute:
Now, from (9), we have a commuting square as shown. Here the left morphism is an epimorphism by construction, while the right morphism is a monomorphism by assumption on . With this, the epi/mono-factorization in Prop. says that there is a diagonal lift which makes both triangles commute.
It remains to see that the lift is unique with just the property of making the top left triangle commute. But this is equivalently the statement that the left morphism is an epimorphism, by Def. .
The equivalence of the first two follows with (Johnstone, lemma 2.1, corollary 2.2). The equivalence of the first and the last is due to Lawvere-Menni 15, lemma 4.1, lemma 4.2.
Elastic toposes
Definition
Let be a cohesive topos (Def. ). Then an elastic topos or differentially cohesive topos over is a sheaf topos which is
-
a cohesive topos over Set,
-
equipped with a quadruple of adjoint functors (Def. ) to of the form
Lemma
(progression of (co-)reflective subcategories of elastic topos)
Let be an elastic topos (Def. ) over a cohesive topos (Def. ):
and write
for the adjoint quadruple exhibiting the cohesion of itself. Then these adjoint functors arrange and decompose as in the following diagram

Proof
The identification
follows from the essential uniqueness of the global section-geometric morphism (Example ). This implies the identifications by essential uniqueness of adjoints (Prop. ).
Definition
(adjoint modalities on elastic topos)
Given an elastic topos (differentially cohesive topos) over (Def. ), composition of the functors in Lemma yields, via Prop. , the following adjoint modalities (Def. )
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. ).
We pronounce these as follows:
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a reduced object;
-
an infinitesimal shape-modal object
is called a coreduced object.
Proposition
(progression of adjoint modalities on elastic topos)
Let be an elastic topos (Def. ) and consider the corresponding adjoint modalities which it inherits
-
for being a cohesive topos, from Def. ,
-
for being an elastic topos, from Def. :
| shape modality | flat modality | sharp modality |
|---|---|---|
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
Then these arrange into the following progression, via the preorder on modalities from Def.
where we display also the bottom adjoint modality (Example ), for completeness.
Proof
We need to show, for all , that
-
is an -modal object (Def. ), hence that
-
is an -modal object (Def. ), hence that
After unwinding the definitions of the modal operators Def. and Def. , and using their re-identification from Lemma , this comes down to the fact that
which holds by Prop. , since is a fully faithful functor and , are (co-)reflectors for it, respectively:
and
Solid toposes
Definition
Let be an elastic topos (Def. ) over a cohesive topos (Def. ). Then a solid topos or super-differentially cohesive topos over is a sheaf topos , which is
-
a cohesive topos over Set (Def. ),
-
an elastic topos over ,
-
equipped with a quadruple of adjoint functors (Def. ) to of the form
hence with and being fully faithful functors (Def. ).
Lemma
(progression of (co-)reflective subcategories of solid topos)
Let be a solid topos (Def. ) over an elastic topos (Def. ):
Then these adjoint functors arrange and decompose as shown in the following diagram:
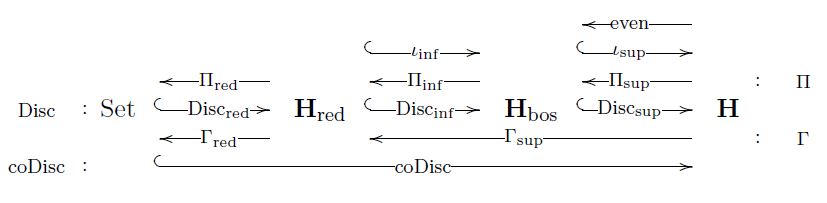
Here the composite adjoint quadruple
exhibits the cohesion of over Set, and the composite adjoint quadruple
exhibits the elasticity of over .
Proof
As in the proof of Prop. , this is immediate by the essential uniqueness of adjoints (Prop. ) and of the global section-geometric morphism (Example ).
Definition
(adjoint modalities on solid topos)
Given a solid topos over (Def. ), composition of the functors in Lemma yields, via Prop. , the following adjoint modalities (Def. )
Since and are fully faithful functors by assumption, these are (co-)modal operators (Def. ) on the cohesive topos, by (Prop. ).
We pronounce these as follows:
| fermionic modality | bosonic modality | rheonomy modality |
|---|---|---|
and we refer to the corresponding modal objects (Def. ) as follows:
-
is called a bosonic object;
-
a -modal object
is called a rheonomic object;
Proposition
(progression of adjoint modalities on solid topos)
Let be a solid topos (Def. ) and consider the adjoint modalities which it inherits
-
for being a cohesive topos, from Def. ,
-
for being an elastic topos, from Def. ,
-
for being a solid topos, from Def. :
| shape modality | flat modality | sharp modality |
|---|---|---|
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
| fermionic modality | bosonic modality | rheonomy modality |
Then these arrange into the following progression, via the preorder on modalities from Def. :
where we are displaying, for completeness, also the adjoint modalities at the bottom and the top (Example ).
Proof
By Prop. , it just remains to show that for all objects
-
is an -modal object, hence ,
-
is a bosonic object, hence .
The proof is directly analogous to that of Prop. , now using the decompositions from Lemma :
and
(…)
Last revised on June 11, 2022 at 10:31:58. See the history of this page for a list of all contributions to it.