nLab internal symmetry
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
Idea
In physics by an “internal symmetry” one broadly means a symmetry other than spacetime symmetry, i.e. a symmetry not due to nor reflecting movement in space and time, but due to “internal degrees of freedom”.
In high energy physics
Notably gauge symmetry is counted as internal symmetry.
Or a spinor field, in the absence of any magnetic field or spin-orbit interaction or any other interaction involving the spin will have a dynamics which is invariant under transformations that just flips the spin, and this is then an internal symmetry.
In solid state physics
In condensed matter theory, internal symmetries are also referred to as “on-site” symmetries, this referring to the sites of the atomic nuclei in the crystal lattice.
For example, the Ising model has an on-site “spin flip”-symmetry , while the Heisenberg model has the full Spin(3)=SU(2)-group acting as an on-site symmetry on the electron spins (cf. CGW11, p. 5).
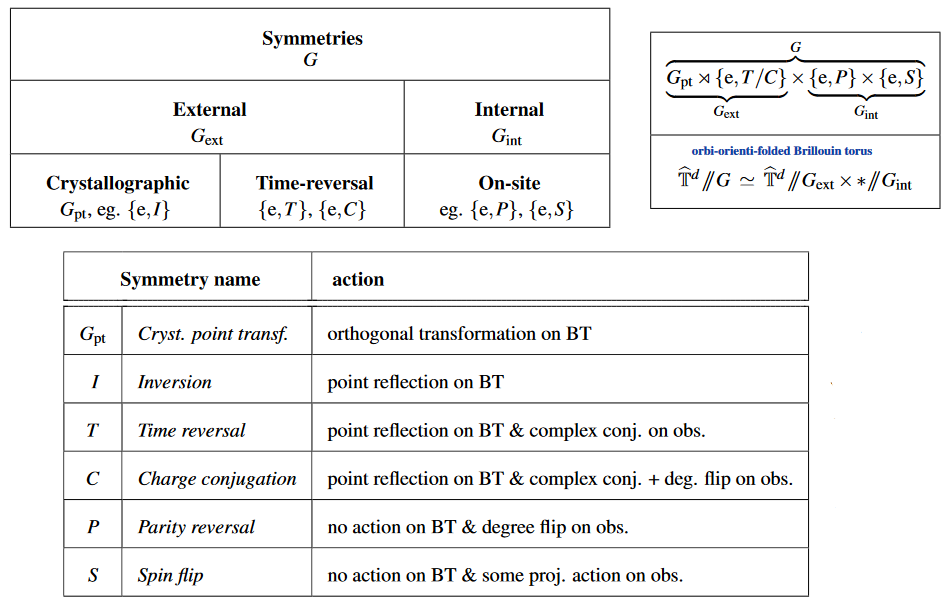 (table from SS 22)
(table from SS 22)
Related concepts
References
Explicit definition of internal symmetry condensed matter theory:
- Charles Zhaoxi Xiong, p. 13 of: Classification and Construction of Topological Phases of Quantum Matter arXiv:1906.02892
Beware that old historical articles (eg. Barlow 1883) used “internal symmetry” to refer to crystallographic symmetry which now is referred to as “spatial symmetry” and regarded as non-internal.
See also:
- Xie Chen, Zheng-Cheng Gu, Xiao-Gang Wen, Classification of gapped symmetric phases in one-dimensional spin systems, Phys. Rev. B 83 035107 (2011) doi:10.1103/PhysRevB.83.035107
Last revised on May 16, 2022 at 17:32:52. See the history of this page for a list of all contributions to it.