nLab lens space

Idea

A lens space is the quotient space

$$L\big(n,\{l_i\}_{i=0}^d\big) \;\coloneqq\; S^{2d+1} / \mathbb{Z}_n \;\coloneqq\; S \big( \mathbb{C}_{l_0} \oplus \cdots \oplus \mathbb{C}_{l_d} \big) / \mathbb{Z}_n$$

of a (2d+1)-dimensional sphere by a free action of a finite cyclic group $\mathbb{Z}_n$ (cf. group actions on spheres); specifically — under the identification of $S^{2d+1}$ with the unit sphere in the real vector space underlying $\mathbb{C}^{d+1}$ — by the action induced from a linear representation of the form

$$\array{ \mathbb{Z}_n \times \mathbb{C}^{d+1} & \overset{ }{ \longrightarrow } & \mathbb{C}^{d+1} \\ \big( [k], (z_0, \cdots, z_{d}) \big) &\mapsto& \Big( \exp\big( 2 \pi \mathrm{i} \tfrac{l_0}{n} \big) \cdot z_0 ,\, \cdots ,\, \exp\big( 2 \pi \mathrm{i} \tfrac{l_d}{n} \big) \cdot z_d \Big) \,m }$$

for natural numbers $l_i \in \mathbb{N}$ coprime to $n$: $gcd(l_i,n) = 1$.

Often this is considered by default for $2d + 1 = 3$, in which case lens spaces are examples of 3-manifolds, and as such are in some sense the simplest after the 3-sphere $S^{3}$ and the product manifold $S^{2} \times S^{1}$ of the 2-sphere with the circle.

Properties

Classification

Theorem

Two lens spaces $L\big(n,\{l_i\}_{i=0}^d\big)$ and $L\big(n,\{l'_i\}_{i=0}^d\big)$ are homotopy equivalent iff there exists a $k\in\mathbb{N}$ with

$$l_0\cdot\ldots\cdot l_d \;\equiv\; k^d l'_0 \cdot \ldots \cdot l'_d \mod n \,.$$

(Olum 1953)

Theorem

Two lens spaces $L\big(n,\{l_i\}_{i=0}^d\big)$ and $L\big(n,\{l'_i\}_{i=0}^d\big)$ are homeomorphic iff there exists a $k\in\mathbb{N}$ and a permutation $\sigma\in Sym_d$ with

$$l_i \;\equiv\; \pm k l'_{\sigma(i)} \mod n$$

for all $i=0,\ldots, d$.

(Brody 1960, Milnor 1966)

In both theorems, the same $n$ for both lens spaces is a necessary condition for them to be homeomorphic or homotopy equivalent as follows with their respective fundamental group.

Cohomology

The ordinary integral cohomology of the lens space $L(n,q) \coloneqq L\big(n,\{q,q, \cdots, q\}\big)$ is [e.g. Maxim, p. 2]:

(1)$$H^i \big( L(n,q) ;\, \mathbb{Z} \big) \;\; \simeq \;\; \left\{ \begin{array}{lcl} \mathbb{Z} &\vert& i = 0 \\ \mathbb{Z}\!/\!q &\vert& i = 2j \leq 2n \\ \mathbb{Z} &\vert& i = 2n + 1 \\ 0 &\vert& \text{otherwise,} \end{array} \right.$$

(where $\mathbb{Z}\!/\!q$ is the cyclic group or order $q$, hence a torsion group).

Homotopy

Lens spaces are the only 3-manifolds with finite, cyclic, non-trivial fundamental group. The reverse direction of this statement (that a 3-manifold with such a fundamental group must be a lens space) is closely related to the Poincaré conjecture.

Lens spaces are important in geometric topology. They offer the simplest examples of smooth manifolds which cannot be distinguished by homotopy theory.

Via Dehn surgery

The 3-dimensional lens space $L(p,q) \coloneqq L(p, \{1,q\})$, for coprime integers $p$ and $q$, can be constructed by Dehn surgery on an unknot with coefficient $-\frac{p}{q}$. One can instead construct $L(p,q)$ by an integral Dehn surgery on the framed ‘generalised Hopf link’

where the unknots have framings $a_{1}$, $\ldots$, $a_{n}$ from left to right, for a continued fraction representation of $-\frac{p}{q}$ as follows.

$$a_{1} - \frac{1}{a_{2} - \frac{1}{\cdots - \frac{1}{a_{n}}}}$$

From EHI 2020

?

Related concepts

• Seifert 3-manifold

References

See also

• Manifold Atlas, Lens spaces.

• Wikipedia, Lens space.

• Neil Strickland, section 9 of: A Bestiary of Topological Objects [pdf, pdf]

In the context of orbifolds:

• Siddhartha Gadgil, Equivariant framings, lens spaces and contact structures, Pacific Journal of Mathematics, Vol. 208 (2003), No. 1, 73–84 (doi:10.2140/pjm.2003.208.73)

• Michel Boileau, Steven Boyer, Radu Cebanu, Genevieve S. Walsh, Section 3 of: Knot commensurability and the Berge conjecture, Geom. Topol. 16 (2012) 625-664 (arXiv:1008.1034)

On classification of lens spaces:

• Paul Olum, Mappings of manifolds and the notion of degree, Ann. of Math. (2) 58 (1953), p. 458–480. JSTOR:1969748

• E. J. Brody, The topological classification of the lens spaces, Ann. of Math. 71 1 (1960) 163–184. [doi:10.2307/1969884, jstor:, MR0116336 (22 #7125) Zbl 0119.18901]

• John Milnor, Whitehead torsion, Bull. Amer. Math. Soc. 72 (1966) 358–426 [doi:10:1090/S0002-9904-1966-11484-2, maths.ed.ac.uk, jstor:bams/1183527946]

On the ordinary cohomology of lens spaces:

• Laurentio-George Maxim, Cohomology of Lens Spaces [pdf, pdf]

Via Dehn surgery:

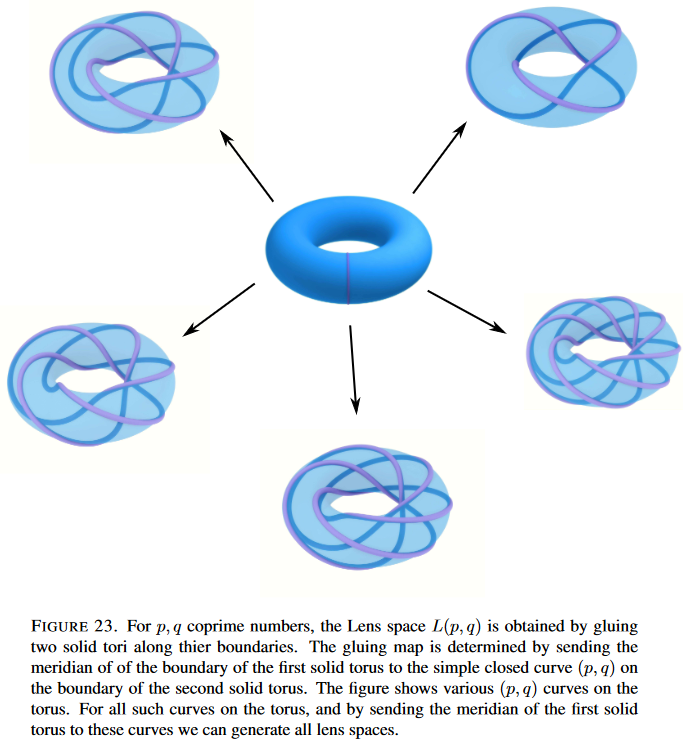
• Mohamed Elhamdadi, Mustafa Hajij, Kyle Istvan, Fig 23 in: Framed Knots, Math Intelligencer 42 (2020) 7–22 [doi:10.1007/s00283-020-09990-0, arXiv:1910.10257]

On lens spaces in cosmic topology:

• Ralf Aurich, Sven Lustig, A survey of lens spaces and large-scale CMB anisotropy, Mon. Not. Roy. Astron. Soc. 424 (2012) 1556-1562 [arXiv:1203.4086, doi:10.1111/j.1365-2966.2012.21363.x]

On the 3d-3d correspondence for lens spaces:

• Du Pei, Chapter III of: 3d-3d correspondence for Seifert manifolds, 2016 (spire:1469350, pdf)