nLab star product

Idea

In deformation quantization of Poisson manifolds the commutative product $\cdot$ of the commutative algebra of functions is replaced by a noncommutative associative product. This is often called a star product and denoted “$\star$”.

An archetypal example is the Moyal star product (example below) that deforms the function algebra on a Poisson vector space, and often “star product” is by default understood to be a Moyal star product. Indeed every star product induced from a constant rank-2 tensor on a vector space is isomorphic to a Moyal star product (prop. below).

More recently also nonassociative “star products” have been proposed to be of interest.

Definition

On finite-dimensional vector spaces

Let $V$ be a finite dimensional vector space and let $\pi \in V \otimes V$ be an element of the tensor product (not necessarily skew symmetric at the moment).

We may canonically regard $V$ as a smooth manifold, in which case $\pi$ is canonically regarded as a constant rank-2 tensor. As such it has a canonical action by forming derivatives on the tensor product of the space of smooth functions:

$$\pi \;\colon\; C^\infty(V) \otimes C^\infty(V) \longrightarrow C^\infty(V) \otimes C^\infty(V) \,.$$

If $\{\partial_i\}$ is a linear basis for $V$, identified, as before, with a basis for $\Gamma(T V)$, then in this basis this operation reads

$$\pi(f \otimes g) \;=\; \pi^{i j} (\partial_i f) \otimes (\partial_j g) \,,$$

where $\partial_i f \coloneqq \frac{\partial f}{\partial x^i}$ denotes the partial derivative of the smooth function $f$ along the $i$th coordinate, and where we use the Einstein summation convention.

For emphasis we write

$$\array{ C^\infty(V) \otimes C^\infty(V) &\overset{prod}{\longrightarrow}& C^\infty(V) \\ f \otimes g &\mapsto& f \cdot g }$$

for the pointwise product of smooth functions.

Definition

(star product induced by constant rank-2 tensor)

Given $(V,\pi)$ as above, then the star product induced by $\pi$ on the formal power series algebra $C^\infty(V) [ [\hbar] ]$ in a formal variable $\hbar$ (“Planck's constant”) with coefficients in the smooth functions on $V$ is the linear map

$$(-) \star_\pi (-) \;\colon\; C^\infty(V)[ [ \hbar ] ] \otimes C^\infty(V)[ [ \hbar ] ] \longrightarrow C^\infty(V)[ [\hbar] ]$$

given by

$$(-) \star_\pi (-) \;\coloneqq\; prod \circ \exp\left( \hbar \pi^{i j} \frac{\partial}{\partial x^i} \otimes \frac{\partial}{\partial x^j} \right)$$

Hence

$$f \star_\pi g \;\coloneqq\; 1 + \hbar \pi^{i j} \frac{\partial f}{\partial x^i} \cdot \frac{\partial g}{\partial x^j} + \hbar^2 \tfrac{ 1 }{2} \pi^{i j} \pi^{k l} \frac{\partial^2 f}{\partial x^{i} \partial x^{k}} \cdot \frac{\partial^2 g}{\partial x^{j} \partial x^{l}} + \cdots \,.$$

Proposition

(star product is associative and unital)

Given $(V,\pi)$ as above, then the star product $(-) \star_\pi (-)$ from def. is associative and unital with unit the constant function $1 \in C^\infty(V) \hookrightarrow C^\infty(V)[ [ \hbar ] ]$.

Hence the vector space $C^\infty(V)$ equipped with the star product $\pi$ is a unital associative algebra.

Proof

Observe that the product rule of differentiation says that

$$\partial_i \circ prod = prod \circ ( \partial_i \otimes id \;+\; id \otimes \partial_i ) \,.$$

Using this we compute as follows:

$$\begin{aligned} (f \star_\pi g) \star_\pi h & = prod \circ \exp( \pi^{i j} \partial_i \otimes \partial_j ) \circ \left( \left( prod \circ \exp( \pi^{k l} \partial_k \otimes \partial_l ) \right) \otimes id \right) (f \otimes g \otimes g) \\ & = prod \circ \exp( \pi^{i j} \partial_i \otimes \partial_j ) \circ (prod \otimes id) \circ \left( \exp( \pi^{k l} \partial_k \otimes \partial_l ) \otimes id \right) (f \otimes g \otimes g) \\ & = prod \circ (prod \otimes id) \circ \exp( \pi^{i j} ( \partial_i \otimes id \otimes \partial_j +id \otimes \partial_i \otimes \partial_j ) \circ \exp( \pi^{k l} \partial_k \otimes \partial_l ) \otimes id (f \otimes g \otimes g) \\ & = prod \circ (prod \otimes id) \circ \exp( \pi^{i j} \partial_i \otimes id \otimes \partial_j ) \circ \exp( \pi^{i j} id \otimes \partial_i \otimes \partial_j ) \circ \exp( \pi^{k l} \partial_k \otimes \partial_l \otimes id ) (f \otimes g \otimes g) \\ & = prod_3 \circ \exp( \pi^{i j} ( \partial_i \otimes \partial_j \otimes id + \partial_i \otimes id \otimes \partial_j + id \otimes \partial_i \otimes \partial_j) ) \end{aligned}$$

In the last line we used that the ordinary pointwise product of functions is associative, and wrote $prod_3 \colon C^\infty(V) \otimes C^\infty(V) \otimes C^\infty(V) \to C^\infty(V)$ for the unique pointwise product of three functions.

The last expression above is manifestly independent of the choice of order of the arguments in the triple star product, and hence it is clear that an analogous computation yields

$$\cdots = f \star_\pi (g \star_\pi h) \,.$$

On polynomial observables in field theory

Definition

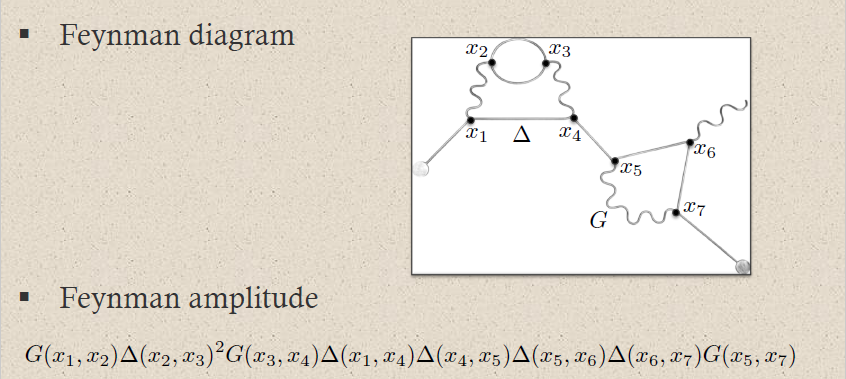
(star products on regular polynomial observables induced from propagators)

Let $(E,\mathbf{L})$ be a free Lagrangian field theory with field bundle $E \overset{fb}{\to} \Sigma$, and let $\Delta \in \Gamma'_\Sigma((E \boxtimes E)^\ast)$ be a distribution of two variables on field histories.

On the off-shell regular polynomial observables with a formal paramater $\hbar$ adjoined consider the bilinear map

$$PolyObs(E)_{reg}[ [\hbar] ] \otimes PolyObs(E)_{reg} [ [ \hbar ] ] \overset{\star_{\Delta}}{\longrightarrow} PolyObs(E)_{reg}[ [\hbar] ]$$

given as in def. , but with partial derivatives replaced by functional derivatives

$$A_1 \star_{\Delta} A_2 \;\coloneqq\; ((-)\cdot(-)) \circ \exp\left( \int_\Sigma \Delta^{a b}(x,y) \frac{\delta}{\delta \mathbf{\Phi}^a(x)} \otimes \frac{\delta}{\delta \mathbf{\Phi}^b(y)} \right) (A_1 \otimes A_2)$$

As in prop. this defines a unital and associative algebra structure.

If the Euler-Lagrange equations of motion induced by the Lagrangian density $\mathbf{L}$ are Green hyperbolic differential equations and if $\Delta$ is a propagator for these differential equations, then this star product algebra descends to the on-shell regular polynomial observables

$$PolyObs(E,\mathbf{L})_{reg}[ [\hbar] ] \otimes PolyObs(E, \mathbf{L})_{reg} [ [ \hbar ] ] \overset{\star_{\Delta}}{\longrightarrow} PolyObs(E, \mathbf{L})_{reg}[ [\hbar] ] \,.$$

(Dito 90, Dütsch-Fredenhagen 00 Dütsch-Fredenhagen 01, Hirshfeld-Henselder 02)

Properties

Equivalences of star products

Proposition

(shift by symmetric contribution is isomorphism of star products)

Let $V$ be a vector space, $\pi \in V \otimes V$ a rank-2 tensor and $\alpha \in Sym(V \otimes V)$ a symmetric rank-2 tensor.

Then the linear map

$$\array{ C^\infty(V) &\overset{\exp\left(\tfrac{1}{2}\alpha \right)}{\longrightarrow}& C^\infty(V) \\ f &\mapsto& \exp\left( \tfrac{1}{2}\hbar \alpha^{i j} \partial_i \partial_j \right) f }$$

constitutes an isomorphism of star product algebras (prop. ) of the form

$$\exp\left(\hbar\tfrac{1}{2}\hbar\alpha \right) \;\colon\; (C^\infty(V)[ [\hbar] ], \star_{\pi}) \overset{\simeq}{\longrightarrow} (C^\infty(V))[ [\hbar] ], \star_{\pi + \alpha}) \,,$$

hence identifying the star product induced from $\pi$ with that induced from $\pi + \alpha$.

In particular every star product algebra $(C^\infty(V)[ [\hbar] ],\star_\pi)$ is isomorphic to a Moyal star product algebra $\star_{\tfrac{1}{2}\pi}$ (example ) with $\tfrac{1}{2}\pi_{skew}^{i j} = \tfrac{1}{2}(\pi^{i j} - \pi^{j i})$ the skew-symmetric part of $\pi$, this isomorphism being exhibited by the symmetric part $2\alpha^{i j} = \tfrac{1}{2}(\pi^{i j} + \pi^{j i})$.

Proof

We need to show that

$$\array{ C^\infty(V)[ [\hbar] ] \otimes C^\infty(V)[ [\hbar] ] & \overset{ \exp\left( \tfrac{1}{2}\hbar \alpha \right) \otimes \exp\left( \tfrac{1}{2}\hbar \alpha \right) }{\longrightarrow}& C^\infty(V)[ [\hbar] ] \otimes C^\infty(V)[ [\hbar] ] \\ {}^{\mathllap{\star_{\pi}}}\downarrow && \downarrow^{\mathrlap{\star_{\pi + \alpha}}} \\ C^\infty(V)[ [\hbar] ] &\underset{\exp\left( \tfrac{1}{2} \alpha \right) }{\longrightarrow}& C^\infty(V)[ [\hbar] ] }$$

hence that

$$prod \circ \exp( \hbar(\pi + \alpha) ) \circ \left( \exp\left( \tfrac{1}{2}\alpha\right) \otimes \exp\left( \tfrac{1}{2}\alpha \right) \right) \;=\; \exp\left( \tfrac{1}{2}\alpha \right) \circ prod \circ \exp( \pi ) \,.$$

To this end, observe that the product rule of differentiation applied twice in a row implies that

$$\partial_i \partial_j \circ prod \;=\; prod \circ \left( (\partial_i \partial_j) \otimes id + id \otimes (\partial_i \partial_j) + \partial_i \otimes \partial_j + \partial_j \otimes \partial_i \right) \,.$$

Using this we compute

$$\begin{aligned} \exp\left( \hbar\tfrac{1}{2}\alpha^{i j} \partial_i \partial_j \right) \circ prod \circ \exp( \hbar \pi^{i j} \partial_{i} \otimes \partial_j ) & = prod \circ \exp\left( \hbar \tfrac{1}{2}\alpha^{i j} \left( (\partial_i \partial_j) \otimes id + id \otimes (\partial_i \partial_j) + \partial_i \otimes \partial_j + \partial_j \otimes \partial_i \right) \right) \circ \exp( \hbar \pi^{i j} \partial_{k} \otimes \partial_l ) \\ & = prod \circ \exp\left( \hbar (\pi^{i j} + \alpha^{i j}) \partial_i \otimes \partial_j \right) \circ \exp\left( \hbar \tfrac{1}{2} \alpha^{i j} (\partial_i \partial_j) \otimes id \hbar \tfrac{1}{2} \alpha^{i j} id \otimes (\partial_i \partial_j) \right) \\ & = prod \circ \exp\left( \hbar (\pi^{i j} + \alpha^{i j}) \partial_i \otimes \partial_j \right) \circ \left( \exp\left( \tfrac{1}{2} \hbar \alpha \right) \otimes \exp\left( \tfrac{1}{2} \hbar \alpha \right) \right) \end{aligned}$$

Integral representations

Proposition

(integral representation of star product)

If $\pi$ skew-symmetric and invertible, in that there exists $\omega \in V^\ast \otimes V^\ast$ with $\pi^{i j}\omega_{j k} = \delta^i_k$, and if the functions $f,g$ admit Fourier analysis (are functions with rapidly decreasing partial derivatives), then their star product (def. ) is equivalently given by the following integral expression:

$$\begin{aligned} \left(f \star_\pi g\right)(x) &= \frac{(det(\omega)^{2n})}{(2 \pi \hbar)^{2n} } \int e^{ \tfrac{1}{i \hbar} \omega((x - \tilde y),(x-y))} f(y) g(\tilde y) \, d^{2 n} y \, d^{2 n} \tilde y \end{aligned}$$

(Baker 58)

Proof

We compute as follows:

$$\begin{aligned} \left(f \star_\pi g\right)(x) & \coloneqq prod \circ \exp\left( \hbar \pi^{i j} \frac{\partial}{\partial x^i} \otimes \frac{\partial}{\partial x^j} \right)(f, g) \\ & = \frac{1}{(2 \pi)^{2n}} \frac{1}{(2 \pi)^{2n}} \int \int \underbrace{ e^{ i \hbar \pi(k,q) } } \underbrace{ e^{i k \cdot (x-y)} f(y) } \underbrace{ e^{i q \cdot (x- \tilde y)} g(\tilde y) } \, d^{2 n} k \, d^{2 n} q \, d^{2 n} y \, d^{2 n} \tilde y \\ & = \frac{1}{(2 \pi)^{2n}} \int \delta\left( x - \tilde y + \hbar \pi \cdot k \right) e^{i k \cdot (x-y)} f(y) g(\tilde y) \, d^{2 n} k \, d^{2 n} y \, d^{2 n} \tilde y \\ & = \frac{1}{(2 \pi)^{2n}} \int \delta\left( x - \tilde y + z \right) e^{ \tfrac{i}{\hbar} \omega(z, (x-y))} f(y) g(\tilde y) \, d^{2 n} z \, d^{2 n} y \, d^{2 n} \tilde y \\ & = \frac{(det(\pi)^{2n})}{(2 \pi \hbar)^{2n} } \int e^{\tfrac{1}{i \hbar}\omega((x - \tilde y),(x-y))} f(y) g(\tilde y) \, d^{2 n} y \, d^{2 n} \tilde y \end{aligned}$$

Here in the first step we expressed $f$ and $g$ both by their Fourier transform (inserting the Fourier expression of the delta distribution from this example) and used that under this transformation the partial derivative $\pi^{a b} \frac{\partial}{\partial\phi^a}{\frac{\partial}{\phi^b}}$ turns into the product with $i \pi^{i j} k_i k_j$ (this prop.). Then we identified again the Fourier-expansion of a delta distribution and finally we applied the change of integration variables $k = \tfrac{1}{\hbar}\omega \cdot z$ and then evaluated the delta distribution.

Next we express this as the groupoid convolution product of polarized sections of the symplectic groupoid. To this end, we first need the following definnition:

Definition

(symplectic groupoid of symplectic vector space)

Assume that $\pi$ is the inverse of a symplectic form $\omega$ on $\mathbb{R}^{2n}$. Then the Cartesian product

$$\array{ && \mathbb{R}^{2n} \times \mathbb{R}^{2n} \\ & {}^{\mathllap{pr_1}}\swarrow && \searrow^{\mathrlap{pr_2}} \\ \mathbb{R}^{2n} && && \mathbb{R}^{2n} }$$

inherits the symplectic structure

$$\Omega \;\coloneqq\; \left( pr_1^\ast \omega - pr_2^\ast \omega \right)$$

given by

$$\begin{aligned} \Omega & = \omega_{i j} d x^i \wedge d x^j - \omega_{i j} d y^i \wedge d y^j \\ & = \omega_{i j} ( d x^i - d y^i ) \wedge ( d x^j + d y^j ) \end{aligned} \,.$$

The pair groupoid on $\mathbb{R}^{2n}$ equipped with this symplectic form on its space of morphisms is a symplectic groupoid.

A choice of potential form $\Theta$ for $\Omega$, hence with $\Omega = d \Theta$, is given by

$$\Theta \coloneqq -\omega_{i j} ( x^i + y^i ) d (x^j - y^j) )$$

Choosing the real polarization spanned by $\partial_{x^i} - \partial_{y^i}$ a polarized section is function $F = F(x,y)$ such that

$$\iota_{\partial_{x^j} - \partial_{y^j}}(d F - \tfrac{1}{i \hbar} \tfrac{1}{4} \Theta F) = 0$$

hence

(1)$$F(x,y) = f\left( \tfrac{x + y}{2} \right) e^{ \tfrac{1}{i \hbar} \omega\left( \tfrac{x - y}{2} , \tfrac{x + y}{2} \right)} \,.$$

Proposition

(polarized symplectic groupoid convolution product of symplectic vector space is given by Moyal star product)

Given a symplectic vector space $(\mathbb{R}^{2n}, \omega)$, then the groupoid convolution product on polarized sections (1) on its symplectic groupoid (def. ), given by convolution product followed by averaging (integration) over the polarization fiber, is given by the star product (def. ) for the corresponding Poisson tensor $\pi \coloneqq \omega^{-1}$, in that

$$\begin{aligned} \int \int F(x,t) G(t,y) \, d^{2n} t \, d^{2n} (x-y) & = (f \star_\pi g)((x+y)/2) \end{aligned} \,.$$

(Weinstein 91, p. 446, Garcia-Bondia & Varilly 94, section V)

Proof

We compute as follows:

$$\begin{aligned} \int \int F(x,t) G(t,y) \, d^{2n} t \, d^{2n} (x-y) & \coloneqq \int \int f((x + t)/2) g( (t + y)/2 ) e^{ \tfrac{1}{i \hbar} \tfrac{1}{4} \omega( x-t, x+t ) + \tfrac{1}{i \hbar} \tfrac{1}{4} \omega(t-y, t + y) } \, d^{2n} t \, d^{2n} (x-y) \\ & = \int \int f(t/2) g( (t - (x - y))/2 ) e^{ \tfrac{1}{i \hbar} \tfrac{1}{4} \omega( (x+y) + (x - y) - t, t ) + \tfrac{1}{i \hbar} \tfrac{1}{4} \omega(t-(x+y), t - (x-y)) } \, d^{2n} t \, d^{2n} (x-y) \\ & = \int \int f(t/2) g( \tilde t / 2) e^{ \tfrac{1}{i \hbar} \tfrac{1}{4} \omega( (x+y) - \tilde t, t ) - \tfrac{1}{i \hbar} \tfrac{1}{4} \omega((x+y)-t, \tilde t) } \, d^{2n} t \, d^{2n} \tilde t \\ & = \int \int f(t) g( \tilde t ) e^{ \tfrac{1}{i \hbar} \tfrac{1}{4} \omega( (x+y) - 2 \tilde t, 2 t ) - \tfrac{1}{ii \hbar} \tfrac{1}{4} \omega((x+y)- 2 t, 2 \tilde t) } \, d^{2n} t \, d^{2n} \tilde t \\ \\ & = \int \int f(t) g(\tilde t ) e^{ \tfrac{1}{i \hbar} \omega\left( \tfrac{1}{2}(x+y) - \tilde t, \tfrac{1}{2}(x + y) - t \right)} \, d^{2n} t \, d^{2n} \tilde t \\ & = (f \star_\omega g)((x+y)/2) \end{aligned}$$

The first line just unwinds the definition of polarized sections from def. , the following lines each implement a change of integration variables and fnally in the last line we used prop. .

Examples

General examples

Some examples of star products as in def. :

Example

If $\pi = 0$ in def. , then the star product $\star_0 = \cdot$ is the plain pointwise product.

Example

(Moyal star product)

If the tensor $\pi$ in def. is skew-symmetric, it may be regarded as a constant Poisson tensor on the smooth manifold $V$. In this case $\star_{\tfrac{1}{2}\pi}$ is called a Moyal star product and the star-product algebra $C^\infty(V)[ [\hbar] ], \star_\pi)$ is called the Moyal deformation quantization of the Poisson manifold $(V,\pi)$.

Wick algebras of normal ordered products

Finite dimensional

Definition

(Kähler vector space)

An Kähler vector space is a real vector space $V$ equipped with a linear complex structure $J$ as well as two bilinear forms $\omega, g \;\colon\; V \otimes_{\mathbb{R}} V \longrightarrow \mathbb{R}$ such that the following equivalent conditions hold:

1. $\omega(J v, J w) = \omega(v,w)$ and $g(v,w) = \omega(v,J w)$;

2. with $V$ regarded as a smooth manifold and with $\omega, g$ regarded as constant tensors, then $(V, \omega, g)$ is an almost Kähler manifold.

Example

(standard Kähler vector spaces)

Let $V \coloneqq \mathbb{R}^2$ equipped with the complex structure $J$ which is given by the canonical identification $\mathbb{R}^2 \simeq \mathbb{C}$, hence, in terms of the canonical linear basis $(e_i)$ of $\mathbb{R}^2$, this is

$$J = (J^i{}_j) \coloneqq \left( \array{ 0 & -1 \\ 1 & 0 } \right) \,.$$

Moreover let

$$\omega = (\omega_{i j}) \coloneqq \left( \array{0 & 1 \\ -1 & 0} \right)$$

and

$$g = (g_{i j}) \coloneqq \left( \array{ 1 & 0 \\ 0 & 1} \right) \,.$$

Then $(V, J, \omega, g)$ is a Kähler vector space (def. ).

The corresponding Kähler manifold is $\mathbb{R}^2$ regarded as a smooth manifold in the standard way and equipped with the bilinear forms $J, \omega g$ extended as constant rank-2 tensors over this manifold.

If we write

$$x,y \;\colon\; \mathbb{R}^2 \longrightarrow \mathbb{R}$$

for the standard coordinate functions on $\mathbb{R}^2$ with

$$z \coloneqq x + i y \;\coloneqq\; \mathbb{R}^2 \to \mathbb{C}$$

and

$$\overline{z} \coloneqq x - i y \;\coloneqq\; \mathbb{R}^2 \to \mathbb{C}$$

for the corresponding complex coordinates, then this translates to

$$\omega \in \Omega^2(\mathbb{R}^2)$$

being the differential 2-form given by

$$\begin{aligned} \omega & = d x \wedge d y \\ & = \tfrac{1}{2i} d z \wedge d \overline{z} \end{aligned}$$

and with Riemannian metric tensor given by

$$g = d x \otimes d x + d y \otimes d y \,.$$

The Hermitian form is given by

$$\begin{aligned} h & = g - i \omega \\ & = d z \otimes d \overline{z} \end{aligned}$$

(for more see at Kähler vector space this example).

Definition

(Wick algebra of a Kähler vector space)

Let $(\mathbb{R}^{2n},\sigma, g)$ be a Kähler vector space (def. ). Then its Wick algebra is the formal power series vector space $\mathbb{C}[ [ \mathbb{R}^{2n} ] ] [ [ \hbar ] ]$ equipped with the star product (def. ) which is given by the bilinear form

(2)$$\pi \coloneqq \tfrac{i}{2} \omega^{-1} + \tfrac{1}{2} g^{-1} \,,$$

hence:

$$\begin{aligned} A_1 \star_\pi A_2 & \coloneqq ((-)\cdot (-)) \circ \exp \left( \hbar\underoverset{k_1, k_2 = 1}{2 n}{\sum}\pi^{a b} \partial_a \otimes \partial_b \right) (A_1 \otimes A_2) \\ & = A_1 \cdot A_2 + \hbar \underoverset{k_1, k_2 = 1}{2n}{\sum}\pi^{k_1 k_2}(\partial_{k_1} A_1) \cdot (\partial_{k_2} A_2) + \cdots \end{aligned}$$

(e.g. Collini 16, def. 1)

Proposition

(star product algebra of Kähler vector space is star-algebra)

Under complex conjugation the star product $\star_\pi$ of a Kähler vector space structure (def. ) is a star algebra in that for all $A_1, A_2 \in \mathbb{C}[ [\mathbb{R}^{2n}] ][ [\hbar] ]$ we have

$$\left( A_1 \star_\pi A_2 \right)^\ast \;=\; A_2^\ast \star_\pi A_1^\ast$$

Proof

This follows directly from that fact that in $\pi = \tfrac{i}{2} \omega^{-1} + \tfrac{1}{2} g^{-1}$ the imaginary part coincides with the skew-symmetric part, so that

$$\begin{aligned} (\pi^\ast)^{a b} & = -\tfrac{i}{2} (\omega^{-1})^{a b} + \tfrac{1}{2} (g^{-1})^{a b} \\ & = \tfrac{i}{2} (\omega^{-1})^{b a} + \tfrac{1}{2} (g^{-1})^{b a} \\ & = \pi^{b a} \,. \end{aligned}$$

Example

(Wick algebra of a single mode)

Let $V \coloneqq \mathbb{R}^2 \simeq Span(\{x,y\})$ be the standard Kähler vector space according to example , with canonical coordinates denoted $x$ and $y$. We discuss its Wick algebra according to def. and show that this reproduces the traditional definition of products of “normal ordered” operators as above.

To that end, consider the complex linear combination of the coordinates to the canonical complex coordinates

$$z \;\coloneqq\; x + i y \phantom{AAA} \text{and} \phantom{AAA} \overline{z} \coloneqq x - i y$$

which we use in the form

$$a^\ast \;\coloneqq\; \tfrac{1}{\sqrt{2}}(x + i y) \phantom{AAA} \text{and} \phantom{AAA} a \;\coloneqq\; \tfrac{1}{\sqrt{2}}(x - i y)$$

(with “$a$” the traditional symbol for the amplitude of a field mode).

Now

$$\omega^{-1} = \frac{\partial}{\partial y} \otimes \frac{\partial}{\partial x} - \frac{\partial}{\partial x} \otimes \frac{\partial}{\partial y}$$

$$g^{-1} = \frac{\partial}{\partial x} \otimes \frac{\partial}{\partial x} + \frac{\partial}{\partial y} \otimes \frac{\partial}{\partial y}$$

so that with

$$\frac{\partial}{\partial z} = \tfrac{1}{2} \left( \frac{\partial}{\partial x} -i \frac{\partial}{\partial y} \right) \phantom{AAAA} \frac{\partial}{\partial \overline{z}} = \frac{1}{2} \left( \frac{\partial}{\partial x} + i \frac{\partial}{\partial y} \right)$$

we get

$$\begin{aligned} \tfrac{i \hbar}{2}\omega^{-1} + \tfrac{\hbar}{2} g^{-1} & = 2 \hbar \frac{\partial}{\partial \overline{z}} \otimes \frac{\partial}{\partial z} \\ & = \hbar \frac{\partial}{\partial a} \otimes \frac{\partial }{\partial a^\ast} \end{aligned}$$

Using this, we find the star product

$$A \star_\pi B \;=\; prod \circ \exp\left( \hbar \frac{\partial}{\partial a} \otimes \frac{\partial }{\partial a^\ast} \right)$$

to be as follows (where we write $(-)\cdot (-)$ for the plain commutative product in the formal power series algebra):

$$\begin{aligned} a \star_\pi a & = a \cdot a \\ a^\ast \star_\pi a^\ast & = a^\ast \cdot a^\ast \\ a^\ast \star_\pi a & = a^\ast \cdot a \\ a \star_\pi a^\ast & = a \cdot a^\ast + \hbar \end{aligned}$$

and so forth, for instance

$$\array{ (a \cdot a ) \star_\pi (a^\ast \cdot a^\ast) & = a^\ast \cdot a^\ast \cdot a \cdot a + 4 \hbar a^\ast \cdot a + \hbar^2 }$$

If we instead indicate the commutative pointwise product by colons and the star product by plain juxtaposition

$$:f g: \;\coloneqq\; f \cdot g \phantom{AAAA} f g \;\coloneqq\; f \star_\pi$$

then this reads

$$\array{ :a a: \, :a^\ast a^\ast: & = : a^\ast a^\ast a a : + 4 \hbar \, : a^\ast a : + \hbar^2 }$$

This is the way the Wick algebra with its operator product $\star_\pi$ and normal-ordered product $:-:$ is traditionally presented.

Infinite-dimensional

Example

(normal-ordered products and time-ordered products)

In cases where $V$ is not finite dimensional, but for instance a space of sections of a linear field bundle, the expression involved in the definition of the star product in def. still may be interpreted as products of distributions, but these only exist if the wavefront sets satisfy Hörmander's criterion.

In these situations it happens that the star product for some Poisson tensor $\tfrac{1}{2}\pi$ is not defined due to wavefront set collision (violation of Hörmander's criterion), but the star product $\star_{\tfrac{1}{2}\pi + \alpha}$ for the tensor $\tfrac{1}{2}\pi + \alpha$ shifted by a symmetric contribition $\alpha$ as in prop. is defined, and serves as the proper stand-in for the non-existing $\star_{\tfrac{1}{2}\pi}$.

This is the case notably for Wick algebras (algebras of quantum observables of free fields): here $\tfrac{1}{2}\pi$ is the causal propagator for which $\star_\pi$ does not exist, and $\pi = \tfrac{1}{2}\pi + \alpha$ is a Wightman propagator, so that $\star_{\pi}$ does exist on microcausal functionals: it is the “normal-ordered product” of quantum observables.

	free field algebra of quantum observables	physics terminology	maths terminology
1)	supercommutative product	$\phantom{AA} :A_1 A_2:$ normal ordered product	$\phantom{AA} A_1 \cdot A_2$ pointwise product of functionals
2)	non-commutative product (deformation induced by Poisson bracket)	$\phantom{AA} A_1 A_2$ operator product	$\phantom{AA} A_1 \star_H A_2$ star product for Wightman propagator
3)		$\phantom{AA} T(A_1 A_2)$ time-ordered product	$\phantom{AA} A_1 \star_F A_2$ star product for Feynman propagator
	perturbative expansion of 2) via 1)	Wick's lemma	Moyal product for Wightman propagator $\Delta_H$ $\begin{aligned} & A_1 \star_H A_2 = \\ & ((-)\cdot (-)) \circ \exp \left( \hbar \int (\Delta_H)^{ab}(x,y) \frac{\delta}{\delta \mathbf{\Phi}^a(x)} \otimes \frac{\delta}{\delta \mathbf{\Phi}^b(y)} \right)(A_1 \otimes A_2) \end{aligned}$
	perturbative expansion of 3) via 1)	Feynman diagrams	Moyal product for Feynman propagator $\Delta_F$ $\begin{aligned} & A_1 \star_F A_2 = \\ & ((-)\cdot (-)) \circ \exp \left( \hbar \int (\Delta_F)^{ab}(x,y) \frac{\delta}{\delta \mathbf{\Phi}^a(x)} \otimes \frac{\delta}{\delta \mathbf{\Phi}^b(y)} \right)(A_1 \otimes A_2) \end{aligned}$

Related concepts

• deformation theory

References

• Giovanni Collini, Fedosov Quantization and Perturbative Quantum Field Theory (arXiv:1603.09626)

In perturbative quantum field theory:

• Michael Dütsch, section 2.1 of From classical field theory to perturbative quantum field theory