nLab Möbius strip

Idea

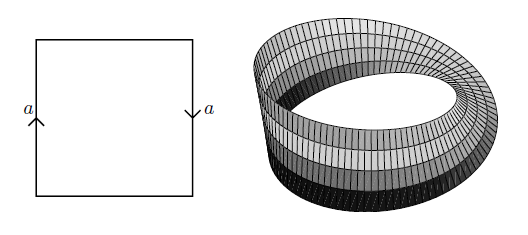
graphics grabbed from Lawson 03

The Möbius strip is the topological space obtained from the “open strip”, hence the square, by gluing two of its opposite sites but after applying half of a full rotation to one of them.

Realizations

As a quotient of the open strip

As a topological space, the Möbius strip is the quotient topological space obtained from the square $[0,1]^2$ by the equivalence relation which identifies two of the opposite sides, but with opposite orientation

$$((x_1,y_1) \sim (x_2,y_2)) \;\;\Leftrightarrow \;\; \left( (x_1,y_1) = (x_2, y_2) \;\text{or}\; \left( x_1 = (1-x_2) \in \{0,1\} \;\text{and}\; y_1 = (1-y_2) \right) \right)$$

As the tautological line bundle over $\mathbb{R}P^1$

Regarded a vector bundle over the circle, the Möbius strip is the tautological line bundle over the 1-dimensional real projective space $\mathbb{P}P^1$.

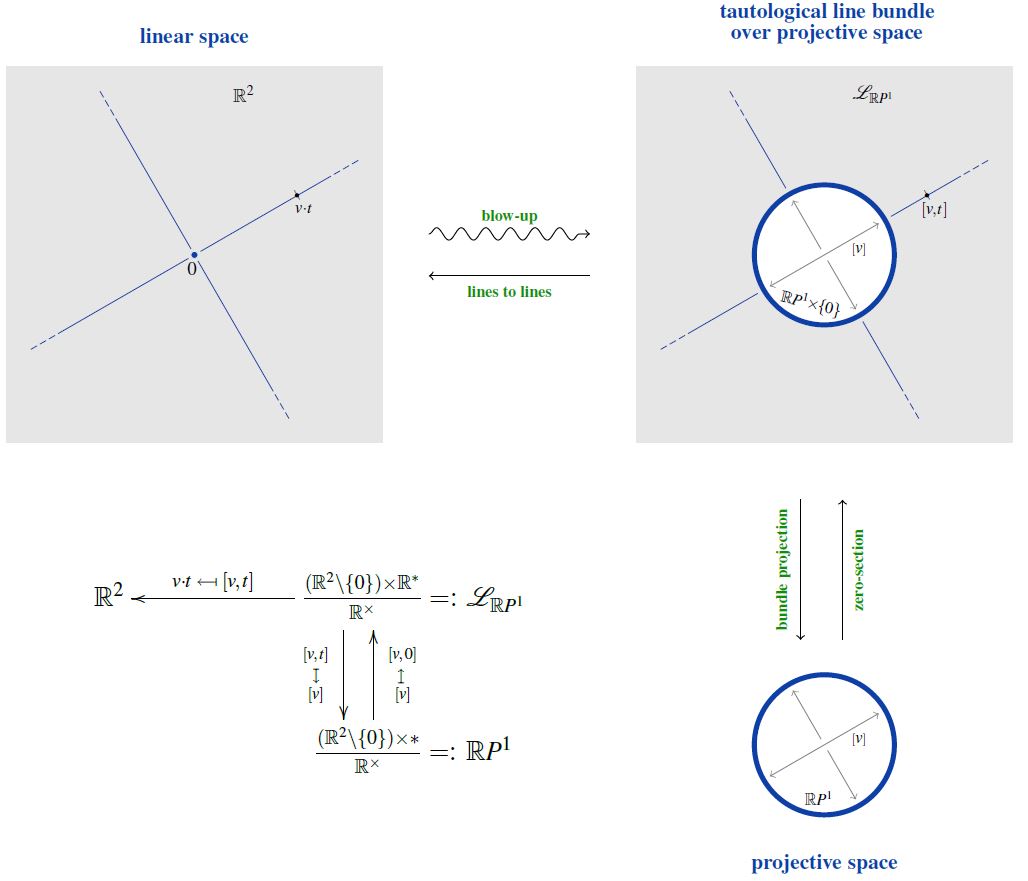
For more discussion of the topological vector bundle structure see this example and this prop.

Properties

Regarded as a manifold, the Möbius strip is among the simplest examples of a manifold that is not orientable.

Regarded as a real vector bundle over the circle, the Möbius strip is among the simplest examples of a non-trivial vector bundle.

Related concepts

• cylinder

• Klein bottle

References

Named after August Möbius.

• Terry Lawson, Topology: A Geometric Approach, Oxford University Press (2003) (pdf)