nLab branched cover
Context
Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Bundles
Context
Classes of bundles
-
vector bundle, 2-vector bundle, (∞,1)-vector bundle
real, complex/holomorphic, quaternionic
Universal bundles
Presentations
Examples
Constructions
Contents
Idea
A “branched” or “ramified” covering space is much like a plain covering space, only that over suitable subspaces, such as isolated points, in the base space – called the branch points or ramification points – sheets of the covering may merge, hence that the group of cover automorphisms has fixed points here.
The archetypical examples are in complex analysis and here the most archetypical example of all is the graph of (any choice of) the square root function on the complex plane, which is a double cover away from the point at the origin, but including the origin it is a branched double cover with branch point that origin
Dually branching is reflected in rings of functions by ramification of ideals.
Notably under the function field analogy one may also understand ramification of ideals in number fields as encoding branched coverings (“over Spec(F1)”)
Examples
Branched covers of -spheres
Every -dimensional PL manifold admits a branched covering of the n-sphere (Alexander 20).
By the Riemann existence theorem, every connected compact Riemann surface admits the structure of a branched cover by a holomorphic function to the Riemann sphere. See there at branched cover of the Riemann sphere.
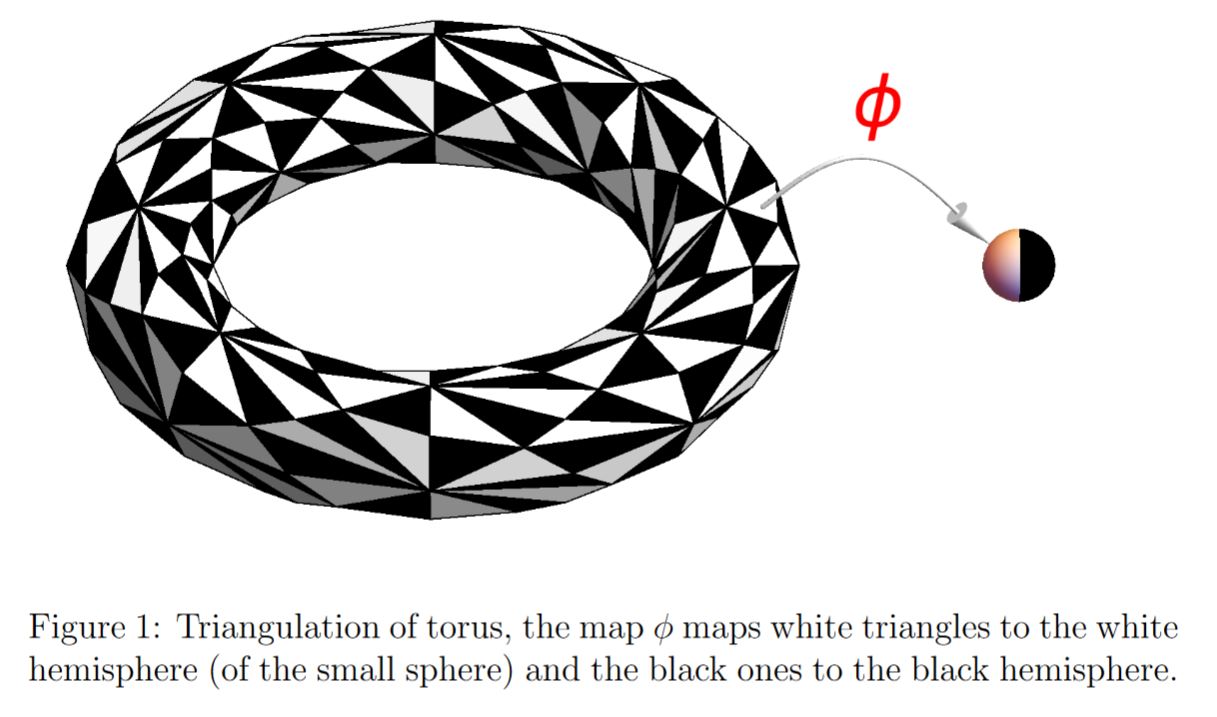
graphics grabbed from Chamseddine-Connes-Mukhanov 14, Figure 1, Connes 17, Figure 11
For 3-manifolds branched covering the 3-sphere see (Montesinos 74).
All PL 4-manifolds are simple branched covers of the 4-sphere (Piergallini 95, Iori-Piergallini 02).
But the n-torus for is not a cyclic branched over of the n-sphere (Hirsch-Neumann 75)
Related concepts
References
General
- Wikipedia, Branched covering
Of arithmetic schemes
- Jürgen Neukirch, Algebraische Zahlentheorie (1992), English translation Algebraic Number Theory, Grundlehren der Mathematischen Wissenschaften 322, 1999 (pdf)
Of manifolds
Every -dimensional PL manifold is a branched cover of the n-sphere:
- James W. Alexander, Note on Riemann spaces, Bull. Amer. Math. Soc. 26 (1920) 370–373
For 3-manifolds branched covering the 3-sphere see
- J. Montesinos, A representation of closed orientable 3-manifolds as 3-fold branched coverings of , Bull. Amer. Math. Soc. 80 (1974), 845-846 (Euclid:1183535815)
All PL 4-manifolds are simple branched covers of the 4-sphere:
-
Riccardo Piergallini, Four-manifolds as 4-fold branched covers of , Topology Volume 34, Issue 3, July 1995 (doi:10.1016/0040-9383(94)00034-I, pdf)
-
Massimiliano Iori, Riccardo Piergallini, 4-manifolds as covers of the 4-sphere branched over non-singular surfaces, Geom. Topol. 6 (2002) 393-401 (arXiv:math/0203087)
For comments on this see also
-
Ali Chamseddine, Alain Connes, Viatcheslav Mukhanov, section 4 of Geometry and the Quantum: Basics, JHEP 12 (2014) 098 (arXiv:1411.0977)
-
Alain Connes, Geometry and the Quantum, Foundations of Mathematics and Physics One Century After Hilbert. Springer 2018. 159-196 (arXiv:1703.02470)
The n-torus for is not a cyclic branched over of the n-sphere:
- U. Hirsch, W. D. Neumann, On cyclic branched coverings of spheres, Math. Ann. (1975) 215: 289 (doi:10.1007/BF01343895)
Relation to orbifolds:
- Benoît Claudon, Gamma-reduction for smooth orbifolds, Manuscripta Mathematica 127, 4 (2008) 521-532 (arXiv:0801.4677)
Last revised on May 5, 2025 at 17:13:54. See the history of this page for a list of all contributions to it.