Schreiber M-Theory from the Superpoint
An article that we have written:
-
M-theory from the superpoint
Letters in Mathematical Physics
108 (2018) 2695–2727
talk slides for Iberian Strings 2017,
talk slides for String Math 2017,
pdf slides and video recording from Higher Structures in M-Theory 2018
exposition: arXiv:1903.02822, doi:10.1002/prop.201910009
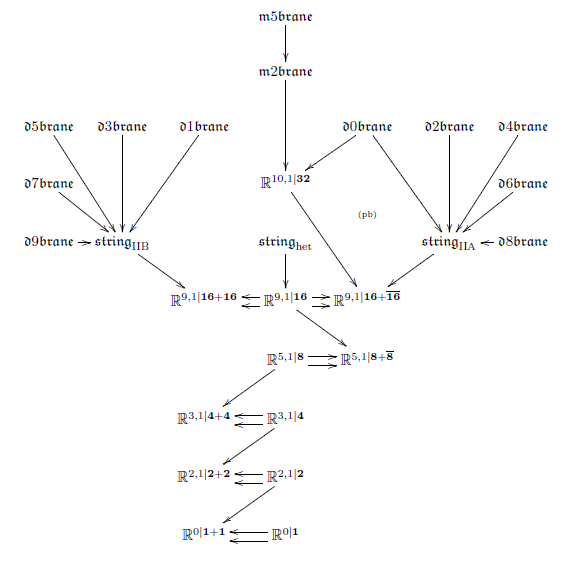
Abstract: The “brane scan” classifies consistent Green-Schwarz superstrings and super-membranes in terms of the invariant cocycles on super-Minkowski spacetimes. The “brane bouquet” generalizes this by consecutively forming the invariant higher central extensions induced by these cocycles, which yields the complete brane content of string theory/M-theory, including the D-branes and the M5-brane, as well as the various duality relations between these. This raises the question whether the super-Minkowski spacetimes themselves arise as maximal invariant central extensions. Here we prove that they do. Starting from the simplest possible super-Minkowski spacetime, the superpoint, which has no Lorentz structure and no spinorial structure, we give a systematic process of consecutive maximal invariant central extensions, and show that it discovers the super-Minkowski spacetimes that contain superstrings, culminating in the 10- and 11-dimensional super-Minkowski spacetimes of string/M-theory and leading directly to the brane bouquet.
Lecture notes:
Related articles:
-
Super Lie n-algebra extensions, higher WZW models and super p-branes
-
T-Duality from super Lie n-algebra cocycles for super p-branes
All summed up in:
Last revised on September 1, 2021 at 15:49:38. See the history of this page for a list of all contributions to it.