Schreiber Super Cartan Geometry
-
next meetings: Feb 16 9:00, Feb 24 10:30
-
location: seminar room at Karlin
(beware that this means we moved location, the previous meetings took place at Maths@CAS, side building)
-
lecture notes: geometry of physics – supergeometry and superphysics
(requires Firefox: free download)
Abstract This seminar gives an introduction to supergeometry and supersymmetry and then leads over to applications in current problems in the mathematical theory of super p-branes. We proceed systematically in the powerful perspective of Cartan geometry, explain its generalization to super Cartan geometry and discover examples of higher Cartan geometry in the process.
After introducing the basics of superalgebra and of motivating supergeometry by Deligne's theorem on tensor categories, we review the classification of Majorana spinors and the construction of super Minkowski spacetime super Lie algebras from these. Then we introduce supergravity as the Cartan geometry locally modeled on these; and we highlight that for the case of 11d supergravity the Einstein equations are equivalent to torsion-free Spin(10,1)-structures.
We discuss then that there is a systematic process in super Lie algebra theory that leads from the superpoint to 11-dimensional supergravity, and explain how this process continues in super L-infinity algebra theory to yield a higher differential geometry of the “super p-branes” of fame in string theory/M-theory.
As a concrete example of much current interest, we derive and explain the construction of “super T-folds” (“doubled” super-geometry) as higher super Cartan geometries locally modeled on a semidirect product of 9d super Minkowski spacetime with the T-duality 2-group.
The first part of the seminar involves fairly standard material, though we mean to amplify some points that are not well reflected in the usual literature. Accordingly, the single textbook that I highly recommend (Castellani-D’Auria-Fré 91) is out of print and seems to be underappreciated. We will also invoke some key results that are not in the textbooks at all, see below at References – Special literature. The last part of the seminar inolves more recent results obtained in joint work with Domenico Fiorenza, Hisham Sati and John Huerta, see below at References – Higher super Cartan geometry.
Contents
Sessions
1) Why Supersymmetry? Deligne’s theorem
In Klein geometry and Cartan geometry the fundamental geometric concept is the symmetry group of the local model space. The model space itself is reconstructed from this as the coset space , the quotient of by the stabilizer subgroup of any one of its points. These symmetry groups are reflected in their categories of representations , which are certain nice tensor categories. In terms of physics via Wigner classification, the irreducible objects in label the possible fundamental particle species on the spacetime . Hence if we regard the tensor category as the actual fundamental concept, then the natural question is that of Tannaka reconstruction: Given any nice tensor category, is it equivalent to for some symmetry group ? For rigid tensor categories over the complex numbers and subject only to a mild size constraint this is answered by Deligne's theorem on tensor categories: all of them are, but only if we allow to be a super-group.
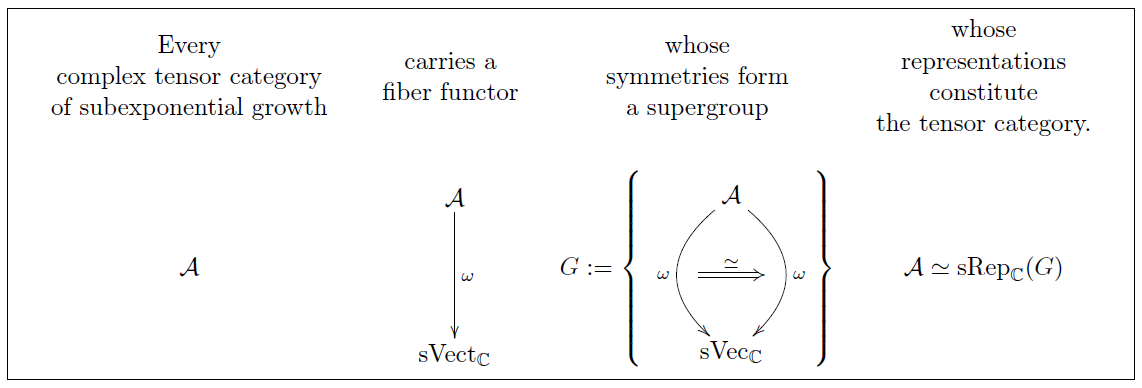
In this session we introduce the basic concepts of superalgebra and supergroups (dually: super-commutative Hopf algebras, EGNO 15, section 9.11). Then we introduce the basic concepts of tensor categories and discuss how categories of representations are examples (e.g. EGNO 15, chapter 2). Finally we discuss aspects of Deligne's theorem on tensor categories following (Deligne 02, Deligne 90), reviewed in (Ostrik 04).
Lecture notes for this session: geometry of physics – superalgebra
2) Supergeometry
In view of Deligne's theorem on tensor categories, Cartan geometry wants to be generalized to supergeometry: “super Cartan geometry”. Just like the building blocks of ordinary differential geometry are the Cartesian spaces with smooth functions between them, so the building blocks of supergeometry are super Cartesian spaces , the Cartesian product of a Cartesian space with a superpoint .
In super-analogy to the theory of generalized smooth spaces this means that all supergeometry takes place in the category of sheaves over these basic objects. For instance a super vector space becomes an ordinary -module when viewed internal to ; similarly a super Lie algebra becomes an ordinary Lie algebra internal to .
Hence the internal perspective of makes all super-structures work in direct parallel to plain structures, with a mathematical machine taking care of the super-aspects being carried along properly.

More in detail, carries a system of adjoint projector-like endofunctors which project out various aspects of super-geometric objects. For instance there is an operation
-
which sends every super-geometric space to its underlying set of points
-
which sends every super-geometric space to its underlying bosonic space;
and various more.
Using these, we may speak of concepts like smooth manifolds and G-structure and torsion of G-structures all internal to , and the result is the generalization of the ordinary such concepts to supermanifolds. This we get to below.
In this session we develop basics of supergeometry and super Lie algebra theory by working in the category of sheaves over superpoints, following (Schwarz 84, Konechny-Schwarz 97, Sachse 08). In particular we see how super vector spaces and super Lie algebras and then super L-infinity algebras are incarnated as functors on the category of finite-dimensional Grassmann algebras with values in ordinary vector spaces, Lie algebras and L-infinity algebras, respectively. Then we add smooth structure by passing to the category of sheaves over all super Cartesian spaces and discuss how higher differential super-geometry is axiomatized using the adjoint progression of modal operators (dcct). As an important example we consider the formulation of frame bundles, of G-structures, and of torsion of a G-structure abstractly (Schreiber-Wellen 16) and for the case of supermanifolds.
Lecture notes for this session: geometry of physics – supergeometry
3) Spacetime supersymmetry
There are many supergroups/super Lie algebras. A natural question to ask is whether any of them singled out as local spacetime symmetry groups?
First of all, the superpoints themselves are naturally supergroups, namely supergroups of “infinitesimal super-translation” along themselves. Hence every super-Lie algebra extension of these yields another natural example.
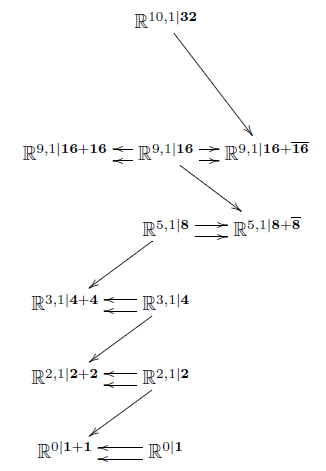
Here a miracle happens (HS): the iterated maximal invariant central extensions of super-points are non-trivial and interesting: The maximal invariant central extension of is the super translation Lie algebra in one dimension, i.e. the worldline of the superparticle. Next, the maximal invariant central extension of is the 2+1-dimensional super Minkowski spacetime , regarded as the supergroup of supersymmetry transformations along itself. This is a super-Lie algebraic extension of ordinary 2+1-dimensional Minkowski spacetime by super-odd directions given by Majorana spinors. Next, the maximal invariant extension of is 3+1-dimensional super Minkowski spacetime . This is the local model spacetime for 4d supergravity. But the process does not stop there: iteratively forming maximal invariant central extensions of the superpoint produces super-Minkowski spacetime in dimensions 3,4,6,10 and 11.
In this session we first review spin representations and in particular Majorana spinor representations, following (CDF, II.7,Figueroa-O’Farrill). We discuss the key properties of the bilinear spinor pairings to -forms, , which will play a central role in all of the following. In particular the pairing to 1-forms (vectors) serves as the odd-odd part of a super Lie bracket that gives the super Poincaré Lie algebras as super-extensions of the ordinary Poincaré Lie algebras. This then defines the super Minkowski spacetimes as the quotients . We discuss the miraculous role that the real normed division algebras play in organizing these supersymmetry algebras (Kugo-Townsend 83, Baez-Huerta 09). Using this we show how to derive the first stages of the iterated tower of invariant extensions of the superpoint (HS).
Lecture notes for this session: geometry of physics – supersymmetry
4) Super-Cartan geometry and 11d Supergravity
Given a smooth manifold, we may ask for a reduction of the structure group of its frame bundle to some group . Furthermore we may ask that the torsion of this “G-structure” vanishes. A wide array of flavors of geometry arise this way, notably Riemannian geometry for . In terms of physics this means that a choice of orthogonal structure – a “vielbein” or “soldering form” is a configuration of the field of gravity.
We may do the same for supermanifolds. Now a vielbein field encodes not just a graviton but also its superpartner, the gravitino. Jointly this is a field configuration in supergravity.
Another miracle happens: for supermanifolds locally modeled on 11-dimenesional super-Minkowski spacetime, then the condition that the orthogonal structure be super- torsion free is already equivalent to the bosonic Einstein equations of 11-dimensional supergravity (Candiello-Lechner 93, Howe 97).
In this session we first review the classical concept of torsion of a G-structure and its interpretation as the identification of infinitesimal neighbourhoods with those of the local model space, due to (Guillemin 65). Then we consider torsion in supergeometry (supertorsion), following (Lott 01), and we explain the torsion constraints in supergravity using the rheonomy principle of (CDF, III.3). Finally we discuss that for 11-dimensional supergravity the vanishing of the supertorsion is already equivaent to the Einstein equations (Candiello-Lechner 93, Howe 97).
5) Fierz identities and Super -Brane geometry
To any super Lie algebra (or super L-infinity algebra ) equipped with an cocycle of degree , there is naturally associated a p-gerbe with connection (the induced higher WZW term) on a higher connected super Lie group (super group stack) Lie integrating. The volume holonomy of this -gerbe is a functional from the space of smooth functions out of closed manifolds of dimension . Regarding this as an action functional, then this defines the dynamics of a p-brane propagating on , in higher dimensional generalization of the propagation of a charged particle (the case of ). For a super-Minkowski group and a Spin-invariant cocycle, then this is called the (higher WZW term of) the Green-Schwarz action functional that defines what it means to have a fundamental super p-brane propagating in some Minkowski spacetime.
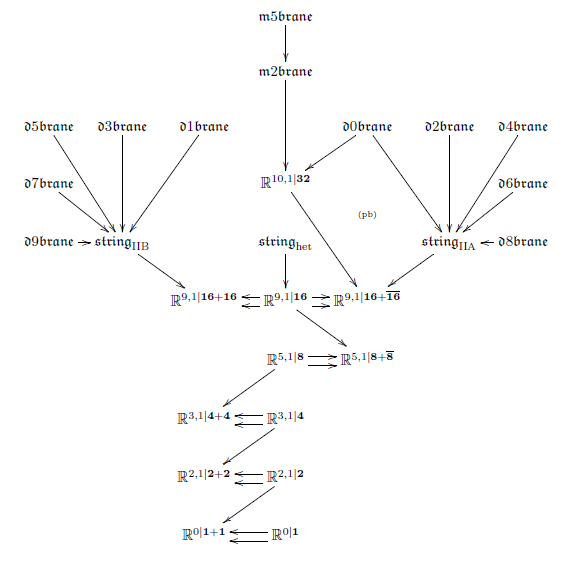
More generally, if we have a Cartan geometry locally modeled on , then we may ask for a -gerbe on , such that it suitably restricts in each tangent space to the above situation. This is directly analogous to the definition of G2-manifolds as 7-manifolds which carry a 3-form that suitably restricts in each tangent space to a fixed 3-form on .
The resulting functional on is a higher “parameterized WZW model” and defines what it means to have a super p-brane propagating on the supermanifold .
Now each such cocycle classifies an extension of super Minkowski spacetime by a super Lie (p+1)-algebra. This may again carry cocycles , defining a super -brane. It turns out that this formalizes the condition that the given -brane may end on the given -brane (FSS 13).
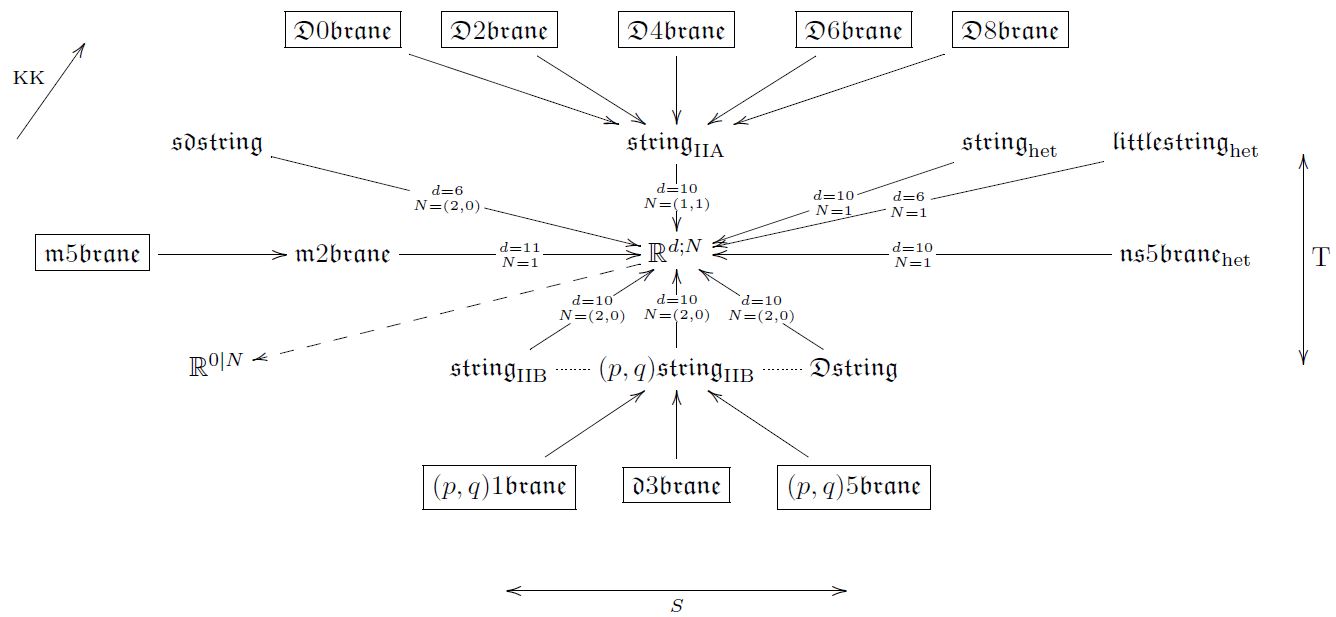
This means that classifying super p-branes propagating on higher super Cartan geometries amounts to classifying the Lie algebra cohomology of super Minkowski spacetimes, and then consecutively classifying the invariant cocycles on the higher super -algebra extensions that these classify. The invariant cocycles all turn out to be spinor bilinar pairings to -forms as above, and hence the condition that they are cocycles is that quartic spinorial expressions of the following form vanish
(or are otherwise equal to similar expressions). Such relations are called Fierz identities. Originally their solutions were classified for just the plain super Minkowski spacetimes, and the result is the “old brane scan”, which sees some, but not all the super -branes in string theory/M-theory. However, if one now passes also to the super-L-infinity algebraic extended super Minkowski spacetimes classified by these cocycles, then one obtains The brane bouquet containing all super -branes.
In this session we first discuss Fierz identities CDF, II.8. Then we use this to discuss the derivation of the “old brane scan” of invariant cocycles on super-Minkowski super Lie algebras (AETW 87) and its extension to extended super-Minkowski spacetimes (CAIB 99, Sakaguchi 00). We explain how the result is naturally interpreted in terms of super L-infinity algebra in The brane bouquet (FSS 13).
Lecture notes for this session: geometry of physics – fundamental super p-branes
6) Super T-folds
A key phenomenon of higher differential geometry is that, due to the presence of homotopy equivalences (weak equivalences) the concept of equality becomes more subtle, and two higher geometries that superficially look very different may turn out to, nevertheless, be equivalent. This is reminiscent of the nature of dualities in string theory, and here we will see that this similarity is not a coincidence.
The archetypical duality in string theory is T-duality, which relates the F1/Dp/NS5-super p-branes of type IIA string theory on a superspacetime which is a circle fiber bundle over a 9d base to those of type IIB string theory on a dual circle fibration with the fiber size inverted in string length units. The F1/Dp-super p-brane charges on both sides of this duality take values in twisted K-theory, and hence the mathematical statement here is that dual circle fibrations of this form induce an equivalence in twisted K-theory. This T-duality equivalence of F1/D-brane charges in twisted K-theory is known in the literature as “topological T-duality”.
It had been suggested in (Hull 04, Hull 06) that therefore there ought to be a generalization of manifolds to “T-folds” or “doubled geometry” which are locally modeled on type IIA/B super-spacetimes, but where diffeomorphisms (e.g. between charts) are promoted to T-duality equivalences.
A mathematical formalization of this idea had been announced (Nikolaus 14). Here the suggestion is that “doubled” spacetimes are really the higher geometric total spaces of principal 2-bundles for a 2-group called the T-duality 2-group.
What however is really necessary is a concept of super T-folds, which has been been left open.
But now the higher super Cartan geometry of super -branes that we discussed in the previous sessions is just so as to apply to such kind of phenomena. It turns out that there is a formalization of double dimensional reduction of super--brane geometries along circle fibrations in higher super Cartan geometry. Applying this to the IIA/B brane geometries from above reveals an equivalence of super L-infinity algebras between the resulting cocycles for IIA/B.
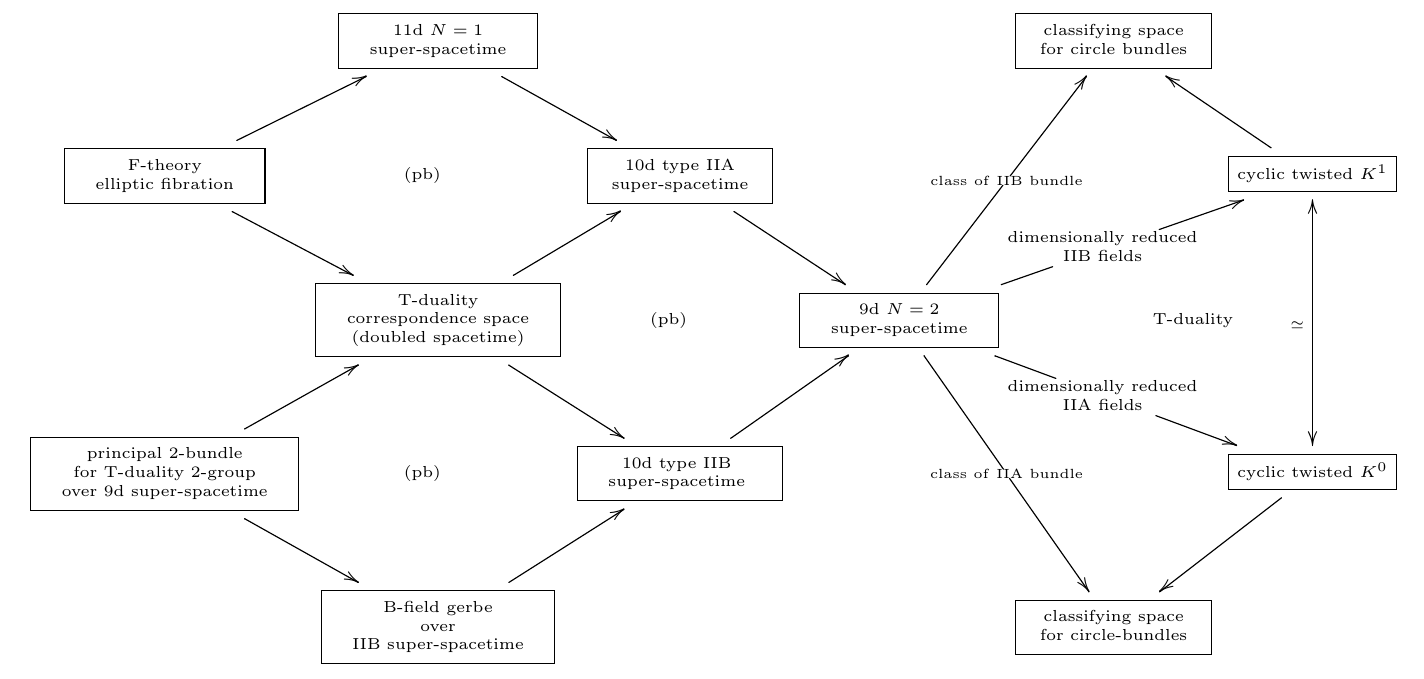
Therefore we may consider the extended super Minkowski spacetime which is the homotopy fiber of (either of) these cocycles
Inspection shows that this homotopy fibr is the local model space for T-folds in “double geometry”. Hence we may study T-folds and their double field theory as a construction in higher super Cartan geometry.
In this session we first recall the fomulation of topological T-duality due to (Bouwknegt-Evslin-Mathai 04a) as well as the alternative formulation due to (Bunke-Schick 05 Bunke-Rumpf-Schick 08). Then we explain the derivation of the supersymmetric version, tangent-space-wise, using the above super L-infinity algebra infinity-Lie algebra cohomology, due to (FSS 16a). Finally we disuss how the T-duality 2-group arises and how it allows to make precise the concept of super T-folds using higher super Cartan geometry.
References
The following first mentions
that might usefully be held on to during the seminar. Then I list
with refernces to original results and to reviews of these. Then I list pointers to my own work with collaborators on
General accounts
An excellent general textbook for our purposes is
- Leonardo Castellani, Riccardo D'Auria, Pietro Fré, Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991)
This is written by physicists in physics style, but the development is careful and thorough, and the “geometric perspective” in the title is nothing but the perspective of higher super Cartan geometry in slight disguise. See also at D'Auria-Fré formulation of supergravity.
Lecture notes closely related to the seminar are in
- Urs Schreiber, Structure Theory for Higher WZW Terms, lectures at Higher Structures in String Theory and Quantum Field Theory, ESI Vienna, November 30-December 4, 2015
More specialized literature
Deligne's theorem on tensor categories is due to
- Pierre Deligne, Catégorie Tensorielle, Moscow Math. Journal 2 (2002) no. 2, 227-248. (pdf)
building on his general work on Tannakian categories
- Pierre Deligne, Catégories Tannakiennes, Grothendieck Festschrift, vol. II, Birkhäuser Progress in Math. 87 (1990) pp.111-195. (pdf)
A brief survey is in
- Victor Ostrik, Tensor categories (after P. Deligne) (arXiv:math/0401347)
and a more comprehensive texbook account is in chapter 9.11 of
- Pavel Etingof, Shlomo Gelaki, Dmitri Nikshych, Victor Ostrik, Tensor categories, Mathematical Surveys and Monographs, Volume 205, American Mathematical Society, 2015 (pdf
))
The observation that supergeometry is naturally regarded as ordinary geometry inside the sheaf topos over superpoints is due to
-
Albert Schwarz, On the definition of superspace, Teoret. Mat. Fiz. (1984) Volume 60, Number 1, Pages 37–42, (russian original pdf)
-
Anatoly Konechny, Albert Schwarz, On -dimensional supermanifolds in Supersymmetry and Quantum Field Theory (Dmitry Volkov memorial volume) Springer-Verlag, 1998, Lecture Notes in Physics, 509 , J. Wess and V. Akulov (editors)(arXiv:hep-th/9706003)
Theory of -dimensional supermanifolds Sel. math., New ser. 6 (2000) 471 - 486
A nice account is in
- Christoph Sachse, A Categorical Formulation of Superalgebra and Supergeometry (arXiv:0802.4067)
Useful discussion of Majorana spinors and the induced supersymmetry algebras includes
-
José Figueroa-O’Farrill, Majorana spinors (pdf)
The close relation between supersymmetry and division algebras was first observed in
- Taichiro Kugo, Paul Townsend, Supersymmetry and the division algebras, Nuclear Physics B, Volume 221, Issue 2 (1983) p. 357-380. (spires, pdf)
A clean survey is in
- John Baez, John Huerta, Division algebras and supersymmetry I, in R. Doran, G. Friedman, Jonathan Rosenberg(eds.) Superstrings, Geometry, Topology, and -algebras, Proc. Symp. Pure Math. 81, AMS, Providence, 2010, pp. 65-80 (arXiv:0909.0551)
and the discussion of the spinor bilinear pairings from this perspective is in
- John Baez, John Huerta, Division algebras and supersymmetry II, Adv. Math. Theor. Phys. 15 (2011), 1373-1410 (arXiv:1003.34360)
The seminal analysis of torsion of G-structures is due to
- Victor Guillemin, The integrability problem for -structures, Trans. Amer. Math. Soc. 116 (1965), 544–560. (JSTOR)
Discussion of torsion of G-structures in the context of supergeometry (supertorsion) is in
- John Lott, The Geometry of Supergravity Torsion Constraints Comm. Math. Phys. 133 (1990), 563–615, (exposition in arXiv:0108125)
An elegant construction of 11-dimensional supergravity, right in the spirit of super Cartan geometry, is due to
- Riccardo D'Auria, Pietro Fré; Geometric Superravity in D=11 and its hidden supergroup, Nuclear Physics B201 (1982) 101-140 (pdf)
This is the main original result on which the D'Auria-Fré formulation of supergravity is based, as laid out in CDF.
The observation that the equations of motion of bosonic solutions of 11-dimensional supergravity are equivalent simply to vanishing of the supertorsion is due to
-
A. Candiello, K. Lechner, Duality in Supergravity Theories, Nucl.Phys. B412 (1994) 479-501 (arXiv:hep-th/9309143)
-
Paul Howe, Weyl Superspace, Physics Letters B
Volume 415, Issue 2, 11 December 1997, Pages 149–155 (arXiv:hep-th/9707184)
Discussion of Fierz identities includes
The classification of the invariant super Lie algebra cocycles on super-Minkowski spacetime, hence that of super p-branes without gauge fields on their worldvolume, is due to
- Anna Achúcarro, Jonathan Evans, Paul Townsend, David Wiltshire, Super -Branes, Phys. Lett. B 198 (1987) 441 (spire)
The extension of this classification to D-branes and to the M5-brane using extended super Minkowski spacetime is due to
-
C. Chryssomalakos, José de Azcárraga, J. M. Izquierdo and C. Pérez Bueno, The geometry of branes and extended superspaces, Nuclear Physics B Volume 567, Issues 1–2, 14 February 2000, Pages 293–330 (arXiv:hep-th/9904137)
-
Makoto Sakaguchi, IIB-Branes and New Spacetime Superalgebras, JHEP 0004 (2000) 019 (arXiv:hep-th/9909143)
The M5-brane cocycle on the “M2-brane extended super-Minkowski spacetime” that appears here has in fact been observed, as a cocycle, all the way back in D’Auria-Fré 82. But there it was seen just as a means for constructing 11-dimensional supergravity. That it indeed gives the higher WZW term in the Green-Schwarz type action functional that defines the fundamental M5-brane has been argued in
- Igor Bandos, Kurt Lechner, Alexei Nurmagambetov, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Covariant Action for the Super-Five-Brane of M-Theory, Phys.Rev.Lett. 78 (1997) 4332-4334 (arXiv:hep-th/9701149)
The observation that super p-branes on curved super spacetimes require definite globalization of super Lie algebra cocycles from Minkowski spacetime over the supermanifold is due to
-
Eric Bergshoeff, Ergin Sezgin, Paul Townsend, Superstring actions in curved superspace, Phys.Lett., B169, 191, (1986) (spire)
-
Eric Bergshoeff, Ergin Sezgin, Paul Townsend, Supermembranes and eleven dimensional supergravity, Phys.Lett. B189 (1987) 75-78, In Mike Duff, (ed.), The World in Eleven Dimensions 69-72 (pdf, spire)
The formulation of topological T-duality is due to
- Peter Bouwknegt, Jarah Evslin, Varghese Mathai, T-Duality: Topology Change from H-flux, Commun.Math.Phys.249:383-415,2004 (hep-th/0306062)
and in an alternative form due to
- Ulrich Bunke, P. Rumpf, Thomas Schick, The topology of -duality for -bundles, Rev. Math. Phys. 18, 1103 (2006). (arXiv:math.GT/0501487)
The suggestion that there ought to be “T-folds” or “doubled geometry” is due to
-
Chris Hull, A Geometry for Non-Geometric String Backgrounds, JHEP0510:065,2005 (arXiv:hep-th/0406102)
-
Chris Hull, Doubled geometry and T-folds JHEP0707:080,2007 (arXiv:hep-th/0605149)
The mathematical formalization of this idea in terms of principal 2-bundles for the T-duality 2-group was claimed in
- Thomas Nikolaus, T-Duality in K-theory and elliptic cohomology, talk at String Geometry Network Meeting, Feb 2014, ESI Vienna (website)
Higher super Cartan geometry
The following articles develop the higher super Cartan geometry that we give an exposition of in the second part of the seminar.
The mathematical foundation of higher supergeometry:
The general idea of The brane bouquet and the general construction of higher WZW terms from higher -cocycles:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields International Journal of Geometric Methods in Modern Physics Volume 12, Issue 02 (2015) 1550018, (arXiv:1308.5264)
The homotopy-descent of the M5-brane cocycle and of the type IIA D-brane cocycles:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory, to appear in Journal of Geometry and Physics (arXiv:1606.03206)
The derivation of supersymmetric topological T-duality, rationally, and of the higher super Cartan geometry for super T-folds:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, T-Duality from super Lie n-algebra cocycles for super p-branes (arXiv:1611.06536)
The derivation of the process of higher invariant extensions that leads from the superpoint to 11-dimensional supergravity:
Last revised on March 2, 2024 at 08:11:17. See the history of this page for a list of all contributions to it.
