Schreiber The brane bouquet

Redirected from "brane bouquet".

Contents

An article that we have written:

$\,$

Followup articles:

Lecture notes

Abstract

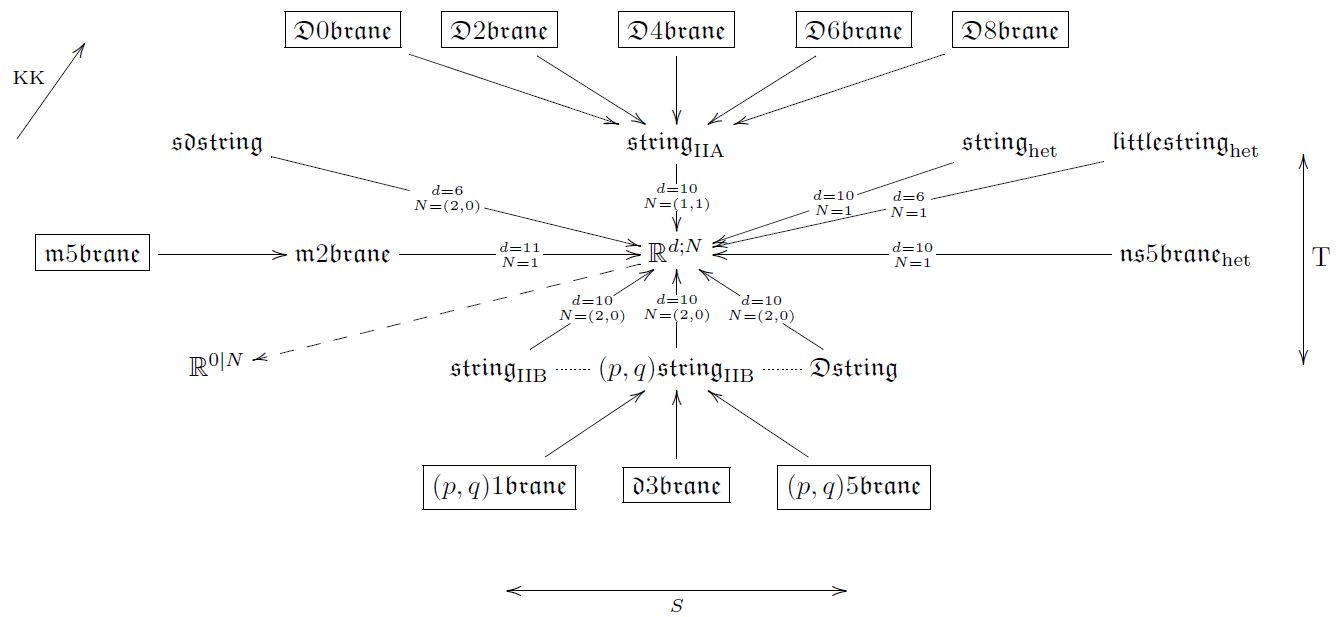
We formalize higher dimensional and higher gauge WZW-type sigma-model local prequantum field theory, and discuss its rationalized/perturbative description in (super-)Lie n-algebra homotopy theory (the true home of the “FDA”-language used in the supergravity literature). We show generally how the intersection laws for such higher WZW-type sigma-model branes (open brane ending on background brane) are encoded precisely in (super-) $L_\infty$ -extension theory and how the resulting “extended (super-)spacetimes” formalize spacetimes containing $\sigma$ -model brane condensates. As an application we prove in Lie $n$ -algebra homotopy theory that the complete super $p$ -brane spectrum of superstring/M-theory is realized this way, including the pure sigma-model branes (the “old brane scan”) but also the branes with tensor multiplet worldvolume fields, notably the D-branes and the M5-brane. For instance the degree-0 piece of the higher symmetry algebra of 11-dimensional spacetime with an M2-brane condensate turns out to be the “M-theory super Lie algebra”. We also observe that in this formulation there is a simple formal proof of the fact that type IIA spacetime with a D0-brane condensate is the 11-dimensional sugra/M-theory spacetime, and of (prequantum) S-duality for type II string theory. Finally we give the non-perturbative description of all this by higher WZW-type $\sigma$ -models on higher super-orbispaces with higher WZW terms in higher differential geometry.

Introductory seminar notes on the topic include the following:

Talk notes on the same topic include the following:

Higher geometric prequantum theory and The Brane Bouquet

notes for a talk at Bayrischzell 2013

(pdf notes)
Super $L_\infty$ -algebras and the Brane Bouquet

(pdf notes)

talk at Higher Algebras and Lie-infinity Homotopy Theory, Luxembourg, June 2013

Abstract What is called the “FDA method” in higher supergravity theory (going back to Riccardo D'Auria and Pietro Fré) is secretly the treatment of super L-∞ algebras via their dual Chevally-Eilenberg super-dg-algebras. In this talk I first introduce super L-∞ algebra cohomology and homotopy fiber sequences of super L-∞ algebras. Then I discuss the diagram of exceptional higher superextensions of the super-translation Lie algebra (super Minkowski spacetime) and show how this classifies the super p-branes in string theory/M-theory together with their open brane intersection laws – a “brane bouquet” refinement of the traditional “brane scan”. Finally I indicate how to each super L-∞ algebra in the brane bouquet there is an associated higher WZW-type sigma model whose fields are tensor multiplets of sigma-model fields combined with higher gauge fields on the worldvolume.
Super $L_\infty$ -extensions and the super $p$ -brane bouquet

talk at Higher Algebras and Lie-infinity Homotopy Theory, Luxembourg, June 26

(example 3 in Synthetic Quantum Field Theory, pdf)