nLab D-brane charge quantization in topological K-theory -- references

D-brane charge quantization in topological K-theory

On the conjectural D-brane charge quantization in topological K-theory:

Origin and basics

The idea that D-branes have Dirac charge quantization in topological K-theory originates with the observation that their charge expressed in RR-field flux densities resembles the image of a Chern character:

Michael Green, Jeffrey A. Harvey, Gregory Moore, I-Brane Inflow and Anomalous Couplings on D-Branes, Class. Quant. Grav. 14 (1997) 47-52 [doi:10.1088/0264-9381/14/1/008, arXiv:hep-th/9605033]
Ruben Minasian, Gregory Moore, K-theory and Ramond-Ramond charge, JHEP 9711:002 (1997) [doi:10.1088/1126-6708/1997/11/002, arXiv:hep-th/9710230]

Further early discussion:

Edward Witten, D-Branes And K-Theory, JHEP 9812:019 (1998) [arXiv:hep-th/9810188, doi:10.1088/1126-6708/1998/12/019]
Petr Hořava, Type IIA D-Branes, K-Theory, and Matrix Theory (1998). (hep-th/9812135).
Daniel Freed, Michael Hopkins, On Ramond-Ramond fields and K-theory, JHEP 0005 (2000) 044 [doi:10.1088/1126-6708/2000/05/044, arXiv:hep-th/0002027]

and with emphasis on the full picture of twisted differential K-theory in:

Daniel Freed, Dirac charge quantization and generalized differential cohomology, Surveys in Differential Geometry, Int. Press, Somerville, MA, 2000, pp. 129–194 (arXiv:hep-th/0011220, doi:10.4310/SDG.2002.v7.n1.a6, spire:537392)

Here:

Green, Harvey & Moore (1997), Minasian & Moore (1997) observe that RR-field flux form-expressions for D-brane charge look like images of K-theory classes under the Chern character;

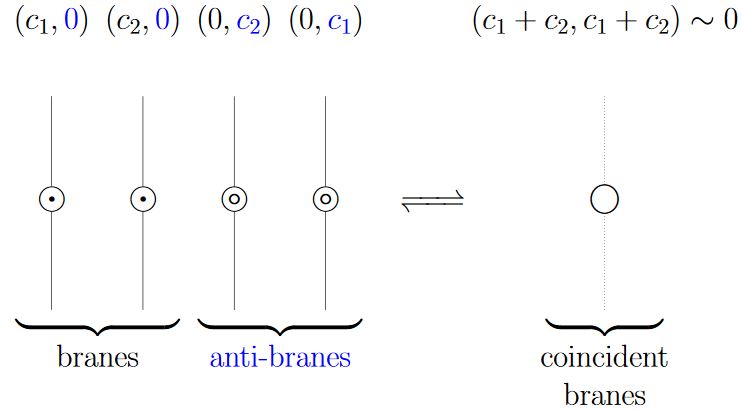
Witten 98, Section 3 adds the observation that the tachyon condensation – which is expected (this is Sen's conjecture from Sen 98) for open strings between D-brane/anti-D-branes – plausibly implements on their Chan-Paton vector bundles the defining equivalence relation (here) of topological K-theory.

Expression of these D-brane K-theory classes via the Atiyah-Hirzebruch spectral sequence:

Juan Maldacena, Gregory Moore, Nathan Seiberg, D-Brane Instantons and K-Theory Charges, JHEP 0111:062,2001 (arXiv:hep-th/0108100)
Jarah Evslin, Hisham Sati, Can D-Branes Wrap Nonrepresentable Cycles?, JHEP0610:050,2006 (arXiv:hep-th/0607045)

Specifically for D-branes in WZW models see

Peter Bouwknegt, A note on equality of algebraic and geometric D-brane charges in WZW models (pdf)

Understanding the solitonic (non-singular) D-branes and their T-duality in K-theory:

Oren Bergman, Eric G. Gimon, Petr Hořava, Brane Transfer Operations and T-Duality of Non-BPS States, JHEP 9904 (1999) 010 [doi:10.1088/1126-6708/1999/04/010, arXiv:hep-th/9902160]

Towards a matrix model taking these K-theoretic effects into account (K-matrix model):

Tsuguhiko Asakawa, Shigeki Sugimoto, Seiji Terashima, D-branes, Matrix Theory and K-homology, JHEP 0203 (2002) 034 [doi:10.1088/1126-6708/2002/03/034, arXiv:hep-th/0108085]

Twisted, equivariant and differential refinement

Discussion of charge quantization in twisted K-theory for the case of non-vanishing B-field:

Witten 98, Sec. 5.3 (for torsion twists)
Peter Bouwknegt, Varghese Mathai, D-branes, B-fields and twisted K-theory, Int. J. Mod. Phys. A 16 (2001) 693-706 [doi:10.1088/1126-6708/2000/03/007, arXiv:hep-th/0002023]

An elaborate proposal for the correct flavour of equivariant KR-theory needed for orientifolds is sketched in:

Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)

Reviews

Kasper Olsen, Richard Szabo, Brane Descent Relations in K-theory, Nucl.Phys. B566 (2000) 562-598 (arXiv:hep-th/9904153)
Kasper Olsen, Richard Szabo, Constructing D-Branes from K-Theory, Adv. Theor. Math. Phys. 3 (1999) 889-1025 (arXiv:hep-th/9907140)
John Schwarz, TASI Lectures on Non-BPS D-Brane Systems (arXiv:hep-th/9908144)
Edward Witten, Overview Of K-Theory Applied To Strings, Int. J. Mod. Phys. A16:693-706, 2001 (arXiv:hep-th/0007175)
Greg Moore, K-Theory from a physical perspective, in: Ulrike Tillmann (ed.) Topology, Geometry and Quantum Field Theory, Proceedings of the 2002 Oxford Symposium in Honour of the 60th Birthday of Graeme Segal, Cambridge University Press (2004) (arXiv:hep-th/0304018, doi:10.1017/CBO9780511526398.011)
Juan José Manjarín, Topics on D-brane charges with B-fields, Int. J. Geom. Meth. Mod. Phys. 1 (2004) (arXiv:hep-th/0405074)
Jarah Evslin, What Does(n’t) K-theory Classify?, Modave Summer School in Mathematical Physics (arXiv:hep-th/0610328, spire:730502)
Stefan Fredenhagen, Physical Background to the K-Theory Classification of D-Branes: Introduction and References (doi:10.1007/978-3-540-74956-1_1), chapter in: Dale Husemoeller, Michael Joachim, Branislav Jurčo, Martin Schottenloher, Basic Bundle Theory and K-Cohomology Invariants, Lecture Notes in Physics, Springer (2008) 1-9 [doi:10.1007/978-3-540-74956-1, pdf]
Fabio Ruffino, Topics on topology and superstring theory (arXiv:0910.4524)
Hisham Sati, Urs Schreiber: Flux Quantization, in Encyclopedia of Mathematical Physics 2nd ed, Elsevier (2024) [arXiv:2402.18473]

Amplification of torsion-charges implied by charge quantization in Ktheory

Volker Braun: K-Theory Torsion [arXiv:hep-th/0005103]
Ilka Brunner, Jacques Distler, Torsion D-Branes in Nongeometrical Phases, Adv. Theor. Math. Phys. 5 (2002) 265-309 [doi:10.4310/ATMP.2001.v5.n2.a3, arXiv:hep-th/0102018]
Ilka Brunner, Jacques Distler, Rahul Mahajan, Return of the Torsion D-Branes, Adv. Theor. Math. Phys. 5 (2002) 311-352 [doi:10.4310/ATMP.2001.v5.n2.a4, arXiv:hep-th/0106262]

Review of D-branes charge seen in KK-theory:

Richard Szabo, D-branes and bivariant K-theory, Noncommutative Geometry and Physics 3 1 (2013): 131. (arXiv:0809.3029)

based on

Rui Reis, Richard Szabo, Geometric K-Homology of Flat D-Branes , Commun. Math. Phys. 266 (2006) 71-122 [arXiv:hep-th/0507043]
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-Branes, RR-Fields and Duality on Noncommutative Manifolds, Commun. Math. Phys. 277 (2008) 643-706 [doi:10.1007/s00220-007-0396-y, arXiv:hep-th/0607020]
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, Noncommutative correspondences, duality and D-branes in bivariant K-theory, Adv. Theor. Math. Phys. 13:497-552, 2009 (arXiv:0708.2648)
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-branes, KK-theory and duality on noncommutative spaces, J. Phys. Conf. Ser. 103 012004 (2008) [doi:10.1088/1742-6596/103/1/012004, arXiv:0709.2128]

In particular (BMRS2) discusses the definition and construction of D-brane charge as a generalized index in KK-theory. The discussion there focuses on the untwisted case. Comments on the generalization of this to topologicall non-trivial B-field and hence twisted K-theory is in

Richard Szabo, D-Branes, Tachyons and K-Homology, Mod. Phys. Lett. A17 (2002) 2297-2316 (arXiv:hep-th/0209210)

Conceptual problems

But there remain conceptual issues with the proposal that D-brane charge is in K-theory, as highlighted in

Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, section 4.5.2 and 4.6.5 of Triples, Fluxes, and Strings, Adv. Theor. Math. Phys. 4 (2002) 995-1186 [arXiv:hep-th/0103170, pdf]
Jarah Evslin, section 8 of: What Does(n’t) K-theory Classify?, Second Modave Summer School in Mathematical Physics [arXiv:hep-th/0610328]

In particular, actual checks of the proposal that D-brane charge is given by K-theory, via concrete computation in boundary conformal field theory, have revealed some subtleties:

Stefan Fredenhagen, Thomas Quella, Generalised permutation branes, JHEP 0511:004 (2005) [arXiv:hep-th/0509153, doi:10.1088/1126-6708/2005/11/004]

It might surprise that despite all the progress that has been made in understanding branes on group manifolds, there are usually not enough D-branes known to explain the whole charge group predicted by (twisted) K-theory. […] it is fair to say that a satisfactory answer is still missing.

The closest available towards an actual check of the argument for K-theory via open superstring tachyon condensation (Witten 98, Section 3) seems to be

Theodore Erler, Analytic Solution for Tachyon Condensation in Berkovits’ Open Superstring Field Theory, JHEP 1311 (2013) 007 [doi:10.1007/JHEP11(2013)007, arXiv:1308.4400]

which, however, concludes (on p. 32) with:

It would also be interesting to see if these developments can shed light on the long-speculated relation between string field theory and the K-theoretic description of D-brane charge $[$ 75, 76, 77]. We leave these questions for future work.

For orbifolds in equivariant K-theory

The proposal that D-brane charge on orbifolds is measured in equivariant K-theory (orbifold K-theory) goes back to

Witten 98, section 5.1

It was pointed out that only a subgroup of equivariant K-theory can be physically relevant in

Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, around (137) of: Triples, Fluxes, and Strings, Adv.Theor.Math.Phys. 4 (2002) 995-1186 (arXiv:hep-th/0103170)

Further discussion of equivariant K-theory for D-branes on orbifolds includes the following:

Hugo García-Compeán, D-branes in orbifold singularities and equivariant K-theory, Nucl.Phys. B557 (1999) 480-504 (arXiv:hep-th/9812226)
Matthias Gaberdiel, Bogdan Stefanski, Dirichlet Branes on Orbifolds, Nucl.Phys.B578:58-84, 2000 (arXiv:hep-th/9910109)
Igor Kriz, Leopoldo A. Pando Zayas, Norma Quiroz, Comments on D-branes on Orbifolds and K-theory, Int. J. Mod. Phys. A 23 (2008) 933-974 [arXiv:hep-th/0703122]
Richard Szabo, Alessandro Valentino, Ramond-Ramond Fields, Fractional Branes and Orbifold Differential K-Theory, Commun.Math.Phys.294:647-702, 2010 (arXiv:0710.2773)

Discussion of real K-theory for D-branes on orientifolds includes the following:

The original observation that D-brane charge for orientifolds should be in KR-theory is due to

Witten 98, section 5

and was then re-amplified in

Sergei Gukov, K-Theory, Reality, and Orientifolds, Commun.Math.Phys. 210 (2000) 621-639 (arXiv:hep-th/9901042)
Oren Bergman, E. Gimon, Shigeki Sugimoto, Orientifolds, RR Torsion, and K-theory, JHEP 0105:047, 2001 (arXiv:hep-th/0103183)

With further developments in

Varghese Mathai, Michael Murray, Daniel Stevenson, Type I D-branes in an H-flux and twisted KO-theory, JHEP 0311 (2003) 053 (arXiv:hep-th/0310164)

Discussion of orbi-orienti-folds using equivariant KO-theory is in

N. Quiroz, Bogdan Stefanski, Dirichlet Branes on Orientifolds, Phys.Rev. D66 (2002) 026002 (arXiv:hep-th/0110041)
Volker Braun, Bogdan Stefanski, Orientifolds and K-theory (arXiv:hep-th/0206158)
H. Garcia-Compean, W. Herrera-Suarez, B. A. Itza-Ortiz, O. Loaiza-Brito, D-Branes in Orientifolds and Orbifolds and Kasparov KK-Theory, JHEP 0812:007, 2008 (arXiv:0809.4238)

Discussion of the alleged K-theory classification of D-brane charge in relation to the M-theory C-field is in

Duiliu-Emanuel Diaconescu, Gregory Moore, Edward Witten, $E_8$ Gauge Theory, and a Derivation of K-Theory from M-Theory, Adv.Theor.Math.Phys.6:1031-1134,2003 (arXiv:hep-th/0005090), summarised in A Derivation of K-Theory from M-Theory (arXiv:hep-th/0005091)