nLab boundary conformal field theory
Context
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The study of conformal field theory on manifolds with boundary, hence conformal boundary field theory, is known as boundary conformal field theory (often abbreviated as BCFT).
For the special case of 2d CFT understood as the quantum field theory on the worldsheet of strings, boundary conformal field theory is the key ingredient of perturbative string theory with prescribed boundary conditions for the open strings. From the target spacetime-perspective these boundary conditions are interpreted as the D-branes that the open strings may “end on”.
In this way 2d BCFT can serve to give an algebraic definition of D-branes, independent of or complementary to their incarnation in the target-spacetime geometry. In particular fractional D-branes may be described this way as boundary conditions for the 2d CFTs describing open strings propagating in orbifolds.
A key tool of BCFT is the boundary state formalism, where one interprets boundary conditions for the open string as coherent states of the corresponding closed string 2d CFT. The physical interpretation of this algebraic fact is that the D-brane, being massive (see also at black brane) emits and absorbs gravitons, which, in string theory, are excitations of the closed string.
It has been argued that, therefore, for sigma-model 2d CFTs the classification of equivalence classes of BCFT boundary states under renormalization group flow should reproduce the expected classification of D-branes by the (equivariant, twisted K-theory) topological K-theory of the target spacetime (Moore 03, section 3).
While this gives, in principle, a precise algebraic definition of D-brane charge from the worldsheet-perspective, in practice it is hard to follow the renormalization group flow of the boundary states. The proposal has been checked in some special cases (e.g. Braun & Schaefer-Nameki 05). Other authors reported some discrepancies (Quiroz-Stefanski 01)
Specifically for fractional D-branes at -orbifold singularities the relevant boundary states are sums of boundary states for each “-twisted sector” of the closed string 2d CFT, consisting of those string configurations that are closed in the covering space up to the action of the element :
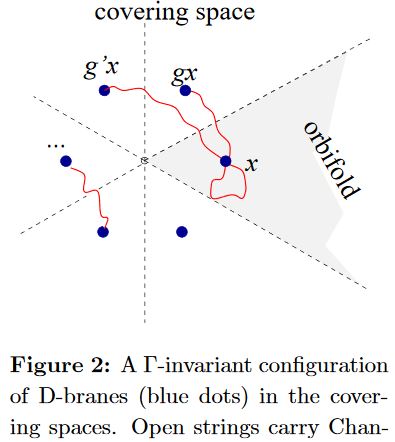
graphics grabbed from BCR 00
Here the coefficient of the -twisted sector in the total boundary state is proprotional to the value of the character of some -representation (e.g. Recknagel-Schomerus 13 (4.102)). This makes it plausible that the RG-flow-equivalence classes of the boundary states for fractional D-branes do coincide with the equivariant K-theory of the orbifold singularity (the representation ring of ).
But maybe this has not yet been actually proven?
Results
There are some mistakes in the literature. A clean account is in Fuchs-Schweigert-Walcher 00, Fuchs-Kaste-Lerche-Lutken-Schweigert 00
Computer scan of Gepner-model compactifications
Discussion of string phenomenology of intersecting D-brane models KK-compactified with non-geometric fibers such that the would-be string sigma-models with these target spaces are in fact Gepner models (in the sense of Spectral Standard Model and String Compactifications) is in (Dijkstra-Huiszoon-Schellekens 04a, Dijkstra-Huiszoon-Schellekens 04b):
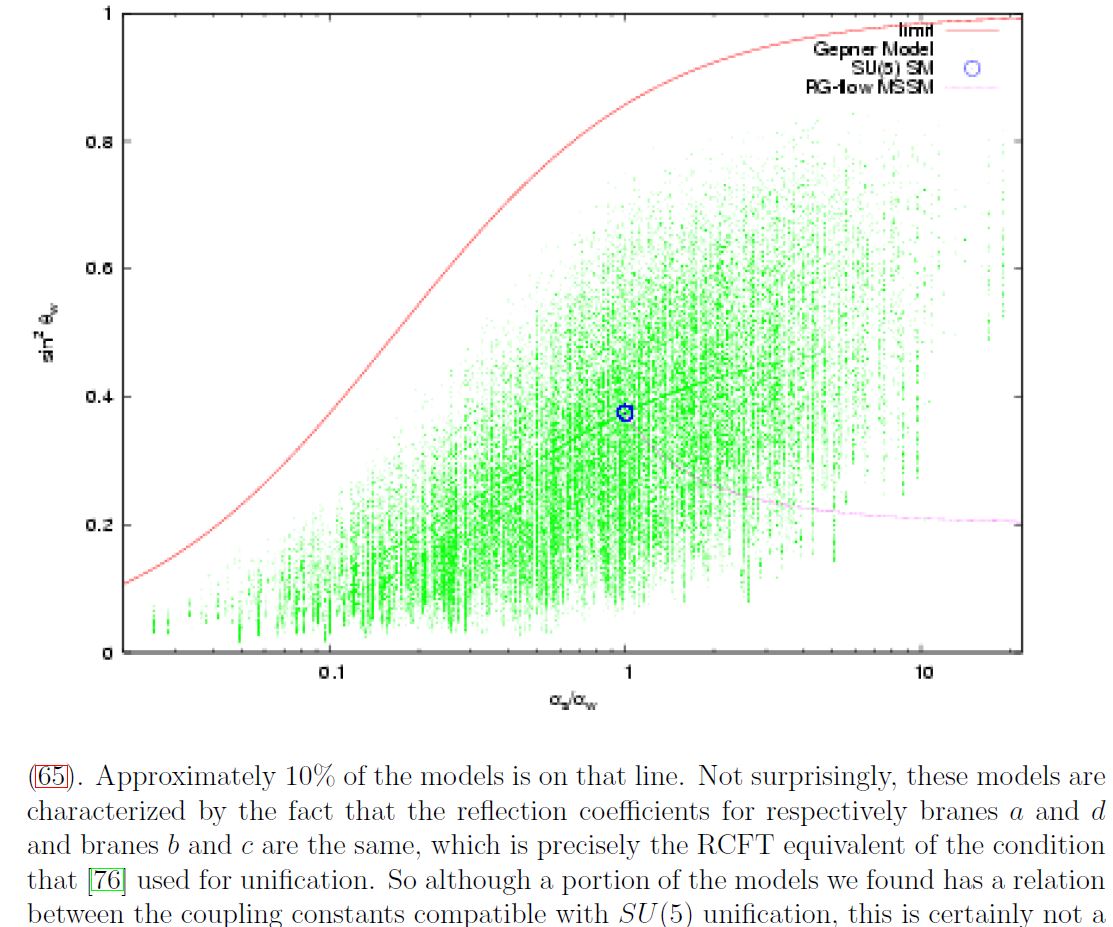
A plot of standard model-like coupling constants in a computer scan of Gepner model-KK-compactification of intersecting D-brane models according to Dijkstra-Huiszoon-Schellekens 04b.
The blue dot indicates the couplings in -GUT theory. The faint lines are NOT drawn by hand, but reflect increased density of Gepner models as seen by the computer scan.
Related concepts
| singularity | field theory with singularities |
|---|---|
| boundary condition/brane | boundary field theory |
| domain wall/bi-brane | QFT with defects |
References
General
The boundary state formalism in BCFT is due to
-
C. G. Callan, C. Lovelace, C. R. Nappi and S. A. Yost, Adding holes and crosscaps to the superstring, Nucl. Phys. B 293 (1987) 83 (doi:10.1016/0550-3213(87)90065-4)
-
C. G. Callan, C. Lovelace, C. R. Nappi and S. A. Yost, Loop corrections to superstring equations of motion, Nucl. Phys. B308 (1988) 221 (pdf)
-
N. Ishibashi, Boundary and Crosscap States in Conformal Field Theories, Mod. Phys. Lett. A4(1989) 251 (pdf)
-
N. Ishibashi and T. Onogi, Open string model building, Nucl. Phys. B318(1989) 239 (doi:10.1016/0550-3213(89)90054-0)
See also
- Andreas Recknagel, Volker Schomerus, Boundary Deformation Theory and Moduli Spaces of D-Branes, Nucl.Phys. B545 (1999) 233-282 (arXiv:hep-th/9811237)
Textbook accounts
-
Ralph Blumenhagen, Erik Plauschinn, Chapter 6 of: Introduction to Conformal Field Theory – With Applications to String Theory, Lecture Notes in Physics 779, Springer (2009) [doi:10.1007/978-3-642-00450-6]
-
Andreas Recknagel, Volker Schomerus, Boundary Conformal Field Theory and the Worldsheet Approach to D-branes, Cambridge 2013 (spire:1308990)
Relation to K-theory
The suggestion that renormalization group flow-equivalence classes of boundary states in 2d BCFT should realize the expected classification of D-brane charge in (equivariant) topological K-theory apparntly goes back to
- Gregory Moore, section 3 of K-Theory from a physical perspective (arXiv:hep-th/0304018)
This has been checked in examples in
-
Volker Braun, Sakura Schafer-Nameki, D-Brane Charges in Gepner Models, J. Math. Phys. 47 (2006) 092304 (arXiv:hep-th/0511100)
-
Igor Kriz, Leopoldo A. Pando Zayas, Norma Quiroz, Comments on D-branes on Orbifolds and K-theory, Int.J.Mod.Phys.A23:933-974, 2008 (arXiv:hep-th/0703122)
A mismatch was claimed in
For rational CFT, WZW models and Gepner models
For rational CFT, specifically Gepner models and WZW models
-
Ilka Brunner, Michael Douglas, Albion Lawrence, Christian Romelsberger, D-branes on the Quintic, JHEP 0008 (2000) 015 (arXiv:hep-th/9906200)
-
Jürgen Fuchs, Christoph Schweigert, J. Walcher, Projections in string theory and boundary states for Gepner models, Nucl.Phys. B588 (2000) 110-148 (arXiv:hep-th/0003298)
(with emphasis on GSO projections)
-
Jürgen Fuchs, P. Kaste, Wolfgang Lerche, C. Lutken, Christoph Schweigert, J. Walcher, Boundary Fixed Points, Enhanced Gauge Symmetry and Singular Bundles on K3, Nucl.Phys.B598:57-72, 2001 (arXiv:hep-th/0007145)
(with emphasis on gauge enhancement on coincident D-branes)
-
Sergei E. Parkhomenko, Free Field Construction of D-Branes in Rational Models of CFT and Gepner Models (arXiv:0802.3445)
-
Giovanni Felder, Jürg Fröhlich, Jürgen Fuchs, Christoph Schweigert, The geometry of WZW branes (arXiv:hep-th/9909030)
On orbifolds
Discussion specifically concerning fractional D-branes on orbifolds includes
-
Lance Dixon, Daniel Friedan, Emil Martinec, Stephen Shenker, The conformal field theory of orbifolds, Nucl. Phys. B 282 (1987) 13. (doi:10.1016/0550-3213(87)90676-6)
-
Diaconescu, Jaume Gomis, Fractional Branes and Boundary States in Orbifold Theories, JHEP 0010 (2000) 001 (arXiv:hep-th/9906242)
-
M. Billo’, B. Craps, F. Roose, Orbifold boundary states from Cardy’s condition, JHEP 0101:038, 2001 (arXiv:hep-th/0011060)
-
N. Quiroz, Bogdan Stefanski Jr, Dirichlet Branes on Orientifolds, Phys.Rev. D66 (2002) 026002 (arXiv:hep-th/0110041)
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Chiral Supersymmetric Standard Model Spectra from Orientifolds of Gepner Models, Phys.Lett. B609 (2005) 408-417 (arXiv:hep-th/0403196)
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Supersymmetric Standard Model Spectra from RCFT orientifolds, Nucl.Phys.B710:3-57,2005 (arXiv:hep-th/0411129)
-
Jaydeep Majumder, Subir Mukhopadhyay, Koushik Ray, Fractional Branes in Non-compact Type IIA Orientifolds, JHEP0611:008, 2006 (arXiv:hep-th/0602135)
Last revised on December 17, 2022 at 12:49:18. See the history of this page for a list of all contributions to it.