nLab type I string theory

Idea

What is called type I string theory is type IIB string theory on orientifold spacetimes, hence on O9-planes.

Its T-dual, called type I’ string theory, is type IIA string theory on O8-planes, which under the duality between M-theory and type IIA string theory is M-theory KK-compactified on the orientifold $S^1 \times S^1 \sslash \mathbb{Z}_2$ (see also M-theory on S1/G_HW times H/G_ADE):

$$\array{ M \\ {}^{ \mathllap{S^1 \times S^1/\mathbb{Z}_2 }}\big\downarrow \\ I' &\underset{T}{\leftrightarrow}& I }$$

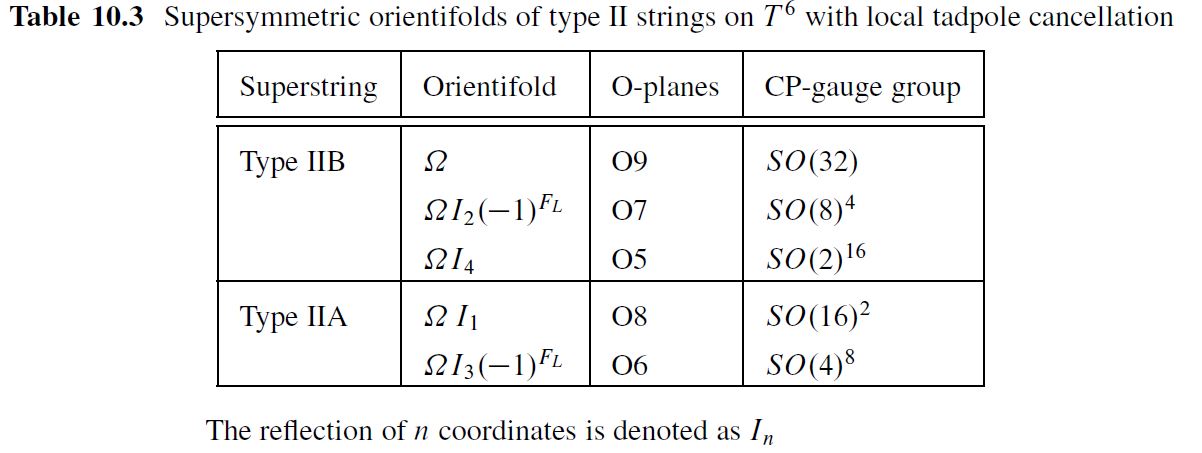
table from BLT 13

Properties

Tadpole cancellation and $SO(32)$-GUT in Type I

For type I string theory on flat (toroidal) target spacetime orientifolds $\mathbb{R}^{9,1}$ (i.e. for type IIB string theory on flat toroidal O9-planes) RR-field tadpole cancellation requires 32 D-branes (see this Remark for counting D-branes in orientifolds) to cancel the O-plane charge of -32 (here).

Under the duality between type I and heterotic string theory this translates to the semi-spin gauge group SemiSpin(32) of heterotic string theory.

Discussion of type-I string phenomenology and grand unified theory based on SO(32) type-I strings: (MMRB 86, Ibanez-Munoz-Rigolin 98, Yamatsu 17).

Tadpole cancellation and $SO(16) \times SO(16)$-GUT in Type I’

For type I’ string theory on flat (toroidal) target spacetime orientifolds $X^{8,1} \times \mathbb{S}^1/\mathbb{Z}_2$ (i.e. for type IIA string theory on two flat toroidal O8-planes) RR-field tadpole cancellation requires 16 D-branes (see this Remark for counting D-branes in orientifolds) on each of the two O8-planes to cancel the total O-plane charge of $-32 = 2 \cdot (-16)$ (here).

Discussion of Spin(16)-GUT phenomenology:

(…)

Orbifolds of type I

Type I’ on toroidal orientifolds with ADE-singularities (e.g. Bergman&Rodriguez-Gomez 12, Sec. 3)

dual to heterotic M-theory on ADE-orbifolds.

(…)

Dualities

String-string dualities

See at duality between type I and heterotic string theory

Horava-Witten theory

One considers the KK-compactification of M-theory on a Z/2-orbifold of a torus, hence of the Cartesian product of two circles

$$\array{ & S^1_A &\times& S^1_B \\ \text{radius}: & R_{11} && R_{10} }$$

such that the reduction on the first factor $S^1_A$ corresponds to the duality between M-theory and type IIA string theory, hence so that subsequent T-duality along the second factor yields type IIB string theory (in its F-theory-incarnation). Now the diffeomorphism which exchanges the two circle factors and hence should be a symmetry of M-theory is interpreted as S-duality in type II string theory:

$$IIB \overset{S}{\leftrightarrow} IIB$$

graphics taken from Horava-Witten 95, p. 15

If one considers this situation additionally with a $\mathbb{Z}/2\mathbb{Z}$-orbifold quotient of the first circle factor, one obtains the duality between M-theory and heterotic string theory (Horava-Witten theory). If instead one performs it on the second circle factor, one obtains type I string theory.

Here in both cases the involution action is by reflection of the circle at a line through its center. Hence if we identify $S^1 \simeq \mathbb{R} / \mathbb{Z}$ then the action is by multiplication by /1 on the real line.

In summary:

M-theory on

• $(S^1_A \sslash \mathbb{Z}_2 ) \times S^1_B$ yields heterotic string theory

• $S^1_A \times \left( S^1_B \sslash \mathbb{Z}_2 \right)$ yields type I' string theory

Hence the S-duality that swaps the two circle factors corresponds to a duality between heterotic E and type I’ string theory. And T-dualizing turns this into a duality between type I and heterotic string theory.

$$\array{ HE &\overset{KK/\mathbb{Z}^A_2}{\leftrightarrow}& M &\overset{KK/\mathbb{Z}^B_2}{\leftrightarrow}& I' \\ \mathllap{T}\updownarrow && && \updownarrow \mathrlap{T} \\ HO && \underset{\phantom{A}S\phantom{A}}{\leftrightarrow} && I }$$

graphics taken from Horava-Witten 95, p. 16

Related concepts

cohomology theories of string theory fields on orientifolds

string theory	B-field	$B$-field moduli	RR-field
bosonic string	line 2-bundle	ordinary cohomology $H\mathbb{Z}^3$
type II superstring	super line 2-bundle	$Pic(KU)//\mathbb{Z}_2$	KR-theory $KR^\bullet$
type IIA superstring	super line 2-bundle	$B GL_1(KU)$	KU-theory $KU^0$
type IIB superstring	super line 2-bundle	$B GL_1(KU)$	KU-theory $KU^1$
type I superstring	super line 2-bundle	$Pic(KU)//\mathbb{Z}_2$	KO-theory $KO$
type $\tilde I$ superstring	super line 2-bundle	$Pic(KU)//\mathbb{Z}_2$	KSC-theory $KSC$

References

General

• Luis Ibáñez, Angel Uranga, section 4.4.3 of: String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012

• Ralph Blumenhagen, Dieter Lüst, Stefan Theisen, Section 9.4 and 10.6 of: Basic Concepts of String Theory Part of the series Theoretical and Mathematical Physics, Springer 2013

Relation to M-theory (via Horava-Witten theory):

• Petr Hořava, Edward Witten, Heterotic and Type I string dynamics from eleven dimensions, Nucl. Phys. B460 (1996) 506 (arXiv:hep-th/9510209)

• Petr Hořava, Edward Witten, Eleven dimensional supergravity on a manifold with boundary, Nucl. Phys. B475 (1996) 94 (arXiv:hep-th/9603142)

A comprehensive discussion of the (differential) cohomological nature of general type II/type I orientifold backgrounds is in

• Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)

with details in

• Daniel Freed, Lectures on twisted K-theory and orientifolds (pdf)

• Jacques Distler, Dan Freed, Greg Moore, Spin structures and superstrings, Surveys in Differential Geometry, Volume 15 (2010) (arXiv:1007.4581, doi:10.4310/SDG.2010.v15.n1.a4)

Related lecture notes / slides include

• Jacques Distler, Orientifolds and Twisted KR-Theory (2008) (pdf)

• Daniel Freed, Dirac charge quantiation, K-theory, and orientifolds, talk at a workshop Mathematical methods in general relativity and quantum field theories, November, 2009 (pdf)

• Greg Moore, The RR-charge of an orientifold, Oberwolfach talk 2010 (pdf, pdf, ppt)

Type I’

Original articles on type I' string theory:

• John Schwarz, Some Properties of Type I’ String Theory, in: Mikhail Shifman (ed.), The Many Faces of the Superworld, pp. 388-397 (2000) (arXiv:hep-th/9907061, doi:10.1142/9789812793850_0023)

• Justin R. David, Avinash Dhar, Gautam Mandal, Probing Type I’ String Theory Using D0 and D4-Branes, Phys. Lett. B415 (1997) 135-143 (arXiv:hep-th/9707132)

Type I’ on toroidal orientifolds with ADE-singularities (dual to heterotic M-theory on ADE-orbifolds):

• Oren Bergman, Diego Rodriguez-Gomez, 5d quivers and their $AdS_6$ duals, JHEP07 (2012) 171 (arxiv:1206.3503)

Phenomenology

Type I string phenomenology and discussion of GUTs based on SO(32) type I strings (see also at heterotic phenomenology):

• H.S. Mani, A. Mukherjee, R. Ramachandran, A.P. Balachandran, Embedding of $SU(5)$ GUT in $SO(32)$ superstring theories, Nuclear Physics B Volume 263, Issues 3–4, 27 January 1986, Pages 621-628 (arXiv:10.1016/0550-3213(86)90277-4)

• Luis Ibáñez, C. Muñoz, S. Rigolin, Aspects of Type I String Phenomenology, Nucl.Phys. B553 (1999) 43-80 (arXiv:hep-ph/9812397)

• Emilian Dudas, Theory and Phenomenology of Type I strings and M-theory, Class. Quant. Grav.17:R41-R116, 2000 (arXiv:hep-ph/0006190)

• Naoki Yamatsu, String-Inspired Special Grand Unification, Progress of Theoretical and Experimental Physics, Volume 2017, Issue 10, 1 (arXiv:1708.02078, doi:10.1093/ptep/ptx135)

Duality

Discussion of duality with heterotic string theory includes the following.

The original conjecture is due to

• Edward Witten, section 5 of String Theory Dynamics In Various Dimensions, Nucl.Phys.B443:85-126 (1995) (arXiv:hep-th/9503124)

More details are then in

• Joseph Polchinski, Edward Witten, Evidence for Heterotic - Type I String Duality, Nucl.Phys.B460:525-540,1996 (arXiv:hep-th/9510169)

Geometric engineering of $D=6$ $\mathcal{N}=(1,0)$ SCFT

On D=6 N=(1,0) SCFTs via geometric engineering on M5-branes/NS5-branes at D-, E-type ADE-singularities, notably from M-theory on S1/G_HW times H/G_ADE, hence from orbifolds of type I' string theory (see at half NS5-brane):

• Michele Del Zotto, Jonathan Heckman, Alessandro Tomasiello, Cumrun Vafa, 6d Conformal Matter, JHEP02(2015)054 (arXiv:1407.6359)

• Davide Gaiotto, Alessandro Tomasiello, Holography for $(1,0)$ theories in six dimensions, JHEP12(2014)003 (arXiv:1404.0711)

• Kantaro Ohmori, Hiroyuki Shimizu, $S^1/T^2$ Compactifications of 6d $\mathcal{N} = (1,0)$ Theories and Brane Webs, J. High Energ. Phys. (2016) 2016: 24 (arXiv:1509.03195)

• Hirotaka Hayashi, Sung-Soo Kim, Kimyeong Lee, Futoshi Yagi, 6d SCFTs, 5d Dualities and Tao Web Diagrams, JHEP05 (2019)203 (arXiv:1509.03300)

• Ibrahima Bah, Achilleas Passias, Alessandro Tomasiello, $AdS_5$ compactifications with punctures in massive IIA supergravity, JHEP11 (2017)050 (arXiv:1704.07389)

Sugimoto string theory

What is now called Sugimoto string theory is a non-supersymmetric version of type I string theory, given by 10d type IIB string theory on an $O9^+$ orientifold (instead of $O9^-$), hence with RR-field tadpole cancellation by 32 anti D9-branes (instead of plain D9-branes), whose gauge group is the symplectic group $USp(32)$.

The original article:

• Shigeki Sugimoto: Anomaly Cancellations in the Type I D9-anti-D9 System and the $USp(32)$ String Theory, Prog. Theor. Phys. 102 (1999) 685-699 [arXiv:hep-th/9905159, doi:10.1143/PTP.102.685]

Further discussion:

• Sanefumi Moriyama: $USp(32)$ String as Spontaneously Supersymmetry Broken Theory, Phys. Lett. B 522 (2001) 177-180 [arXiv:hep-th/0107203, doi:10.1016/S0370-2693(01)01278-3]

• Hector Parra de Freitas, p. 166 of: String Compactifications with Half-maximal Supersymmetry, PhD thesis, Université Paris-Saclay (2023) [hal/tel-04234221, pdf]

• Vittorio Larotonda, Ling Lin: Anomaly Inflow and Gauge Group Topology in the 10d Sugimoto String Theory [arXiv:2412.17894]