nLab BFSS matrix model
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The BFSS matrix model (Banks-Fischler-Shenker-Susskind 96, Seiberg 97) is the description of the worldline dynamics of interacting D0-branes. In the large N limit of a large number of D0-branes this is supposed to encode the strong coupling limit of type IIA string theory known as M-theory at least in certain corners of its moduli space.
The BFSS model is a limiting case of the BMN matrix model, which improves on some of its shortcomings (see the Open problems below).
The BFSS matrix model was argued to arise in several seemingly rather different (but apparently secretly equivalent) ways:
-
as the worldline theory of a large number of D0-branes in type IIA string theory,
-
as the Kaluza-Klein compactification of 10d super Yang-Mills theory to 1+0 space dimensions,
-
as a certain non-commutative regularization of the light-cone gauge quantization of the Green-Schwarz sigma-model for the M2-brane (Nicolai-Helling 98, Dasgupta-Nicolai-Plefka 02).
In this picture matrix blocks around the diagonal correspond to blobs of membrane, while off-diagonal matrix elements correspond to thin tubes of membrane connecting these blobs.
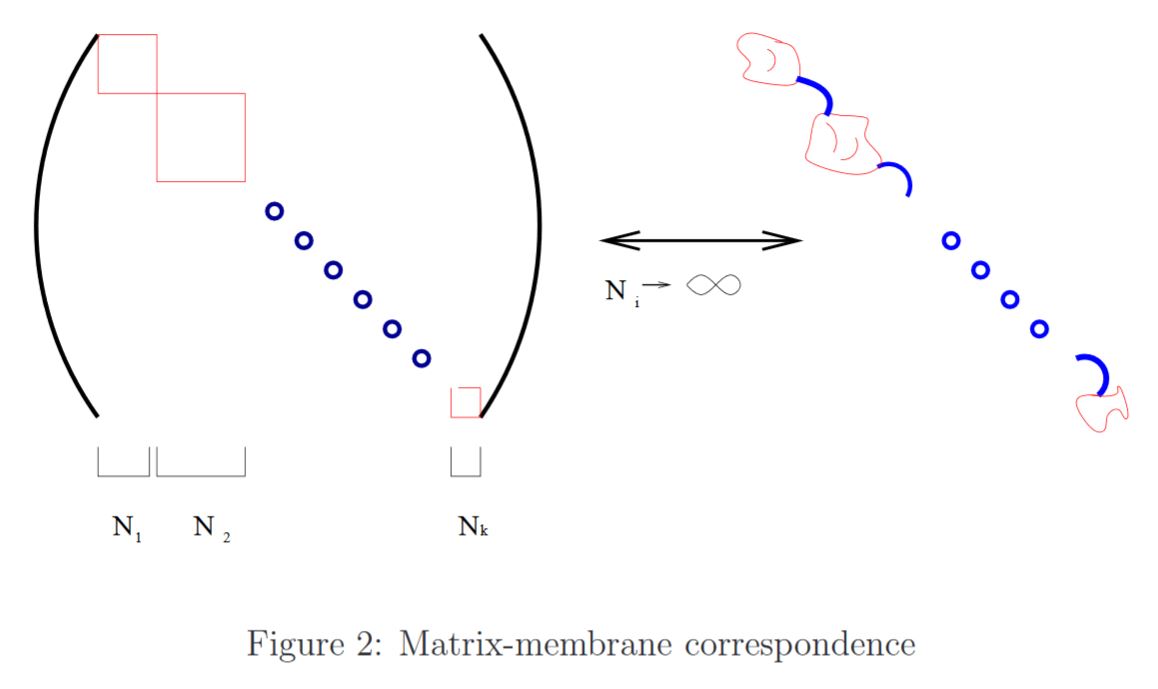
graphics grabbed from Dasgupta-Nicolai-Plefka 02
In any case, the BFSS matrix model ends up being a quantum mechanical system whose bosonic degrees of freedom are a set of 9+1 large matrices. These play the role of would-be coordinate functions and their eigenvalues may be interpreted as points in a non-commutative spacetime thus defined.
There is also the IKKT matrix model, which takes this one step further by reducing one dimension further down to D(-1)-branes in type IIB string theory.
See also at membrane matrix model.
Open problems
General
In the 1990s there was much excitement about the BFSS model (and then its cousin, the IKKT matrix model), as people hoped it might provide a definition of M-theory, whose formulation remains elusive. It is from these times that Edward Witten changed the original suggestion that “M” is for “magic, mystery and membrane” to the suggestion that it is for “magic, mystery and matrix”. (See Witten’s 2014 Kyoto prize speech, last paragraph.)
However, while the BFSS matrix model clearly sees something M-theoretic, just as clearly it is not the full answer. Notably it needs for its definition an ambient asymptotic Minkowski spacetime background, a light cone limit and a peculiar scaling of string coupling over string length, all of which means that it pertains to a particular corner of a full theory.
From Nicolai-Helling 1998, p. 2:
Despite the recent excitement, however, we do not think that M(atrix) theory and the supermembrane in their present incarnation are already the final answer in the search for M-Theory, even though they probably are important pieces of the puzzle. There are still too many ingredients missing that we would expect the final theory to possess. For one thing, we would expect a true theory of quantum gravity to exhibit certain pregeometrical features corresponding to a “dissolution” of space-time and the emergence of some kind of non-commutative geometry at short distances; although the matrix model does achieve that to some extent by replacing commuting coordinates by non-commuting matrices, it seems to us that a still more radical departure from conventional ideas about space and time may be required in order to arrive at a truly background independent formulation (the matrix model “lives” in nine flat transverse dimensions only). Furthermore, there should exist some huge and so far completely hidden symmetries generalizing not only the duality symmetries of extended supergravity and string theory, but also the principles underlying general relativity.
From Mohammed-Murugan-Nastase 2010, p. 6:
If Matrix theory is to correctly describe M-theory (and its dimensional reduction to type IIA string theory) then it should be able to describe all D−branes in the theory and not just D2−branes. For example, a D4−brane wrapping an was found in [9], following the earlier works of [10, 11], but the solution is not without several unresolved subtleties. In general, finding the complete spectrum of D−branes from Matrix theory remains a very difficult problem. The D2− and D4−branes already found are reductions to ten dimensions of M2− and M5−branes, and while they are a minimum necessary for the spectrum of M-theory, they are by no means sufficient. Indeed, we would also need to find a D6−brane, coming from an eleven dimensional KK monopole, and a D8−brane.
Then, even assuming that all the crucial cohomological aspects of D-brane and M-brane charges (in twisted differential K-theory, twisted cohomotopy etc.) are secretly encoded in the matrix model, somehow, none of this is manifest, making the matrix model spit out numbers about a conceptually elusive theory in close analogy to how lattice QCD produces numbers without informing us about the actual conceptual nature of confined hadron physics.
A similar assessment has been given by Greg Moore, from pages 43-44 of his Physical Mathematics and the Future (2014, here):
A good start with defining M-theory was given by the Matrix theory approach of Banks, Fischler, Shenker and Susskind. We have every reason to expect that this theory produces the correct scattering amplitudes of modes in the 11-dimensional supergravity multiplet in 11-dimensional Minkowski space - even at energies sufficiently large that black holes should be created. (This latter phenomenon has never been explicitly demonstrated). But Matrix theory is only a beginning and does not give us the whole picture of M-theory. The program ran into increasing technical difficulties when more complicated compactifications were investigated. (For example, compactification on a six-dimensional torus is not very well understood at all. …). Moreover, to my mind, as it has thus far been practiced it has an important flaw: It has not led to much significant new mathematics.
If history is a good guide, then we should expect that anything as profound and far-reaching as a fully satisfactory formulation of M-theory is surely going to lead to new and novel mathematics. Regrettably, it is a problem the community seems to have put aside - temporarily. But, ultimately, Physical Mathematics must return to this grand issue.
Ground state
There are furcher technical open issues, such as the open question whether the theory has a decent ground state the way it needs to have to make sense (see the references below).
Related concepts
matrix models for brane dynamics:
| D-brane | matrix model |
|---|---|
| D0-brane | BFSS matrix model, BMN matrix model |
| D(-1)-brane | IKKT matrix model |
| D4-brane | nuclear matrix model |
| M-brane | matrix model |
|---|---|
| D2-brane | membrane matrix model |
See also:
References
General
First inkling of matrix models from the large N limit of QCD:
-
Tohru Eguchi, Hikaru Kawai, Reduction of Dynamical Degrees of Freedom in the Large- Gauge Theory, Phys. Rev. Lett. 48, 1063 (1982) (spire:176459, doi:10.1103/PhysRevLett.48.1063)
-
A. Gonzalez-Arroyo, M. Okawa, A twisted model for large lattice gauge theory, Physics Letters B Volume 120, Issues 1–3, 6 January 1983, Pages 174-178 (doi:10.1016/0370-2693(83)90647-0)
-
A. Gonzalez-Arroyo, M. Okawa, Twisted-Eguchi-Kawai model: A reduced model for large- lattice gauge theory, Phys. Rev. D 27, 2397 (1983) (doi:10.1103/PhysRevD.27.2397)
The original articles on the BFSS matrix model:
-
Tom Banks, Willy Fischler, Stephen Shenker, Leonard Susskind, M Theory As A Matrix Model: A Conjecture, Phys. Rev. D 55 (1997) [doi:10.1103/PhysRevD.55.5112, arXiv:hep-th/9610043]
-
Leonard Susskind, Another Conjecture about M(atrix) Theory (arXiv:hep-th/9704080)
(argument for small N-validity)
and with more details on the discrete light front quantization involved:
-
Ashoke Sen, D0 Branes on and Matrix Theory, Adv. Theor. Math. Phys. 2 (1998) 51-59 [arXiv:hep-th/9709220]
-
Nathan Seiberg, Why is the Matrix Model Correct?, Phys. Rev. Lett. 79 (1997) 3577-3580 [arXiv:hep-th/9710009, doi:10.1103/PhysRevLett.79.3577]
-
Adel Bilal, DLCQ of M-Theory as the Light-Like Limit, Phys. Lett. B 435 (1998) 312-318 [arXiv:hep-th/9805070, doi:10.1016/S0370-2693(98)00811-9]
In relation to U-duality:
- Shmuel Elitzur, Amit Giveon, David Kutasov, Eliezer Rabinovici: Algebraic Aspects of Matrix Theory on , Nucl. Phys. B 509 (1998) 122-144 [arXiv:hep-th/9707217, doi:10.1016/S0550-3213(97)00622-6]
In view of flat space holography:
- Leonard Susskind, Holography in the flat space limit, AIP Conf.Proc. 493 (1999) 1, 98-112, (spire, arXiv:hep-th/9901079, doi:10.1063/1.1301570)
Review:
-
Adel Bilal, M(atrix) Theory : a Pedagogical Introduction, Fortsch. Phys. 47 (1999) 5-28 [arXiv:hep-th/9710136, doi:10.1002/(SICI)1521-3978(199901)47]
-
Tom Banks, Matrix Theory, Nucl. Phys. Proc. Suppl. 67 (1998) 180-224 [arXiv:hep-th/9710231, doi:10.1016/S0920-5632(98)00130-3]
-
Washington Taylor, M(atrix) Theory: Matrix Quantum Mechanics as a Fundamental Theory, Rev. Mod. Phys. 73 (2001) 419-462 [arXiv:hep-th/0101126]
-
Luca Carlevaro: Three approaches to M-theory, PhD thesis (2006) [hdl:123456789/16186, pdf, spire:1253257]
-
Badis Ydri, Review of M(atrix)-Theory, Type IIB Matrix Model and Matrix String Theory [arXiv:1708.00734), published as: Matrix Models of String Theory, IOP 2018 (ISBN:978-0-7503-1726-9]
-
Juan Maldacena: The BFSS conjecture, a review, talk at Strings 2024 (2024) [indico:5975486, pdf]
Review in the context of the holographic principle:
- Juan Maldacena, A simple quantum system that describes a black hole [arXiv:2303.11534, inspire:2644529]
A review of further developments:
- David Berenstein, Classical dynamics and thermalization in holographic matrix models, talk at Leiden, October (2012) [pdf]
See also
-
Paul Townsend, M(embrane) theory on , Nucl. Phys. Proc. Suppl. 68 (1998) 11-16 [arXiv:hep-th/9708034]
-
Chris D. A. Blair, Johannes Lahnsteiner, Niels A. Obers, Ziqi Yan. Unification of Decoupling Limits in String and M-theory [arXiv:2311.10564]
-
Henry W. Lin, Zechuan Zheng: Bootstrapping Ground State Correlators in Matrix Theory, Part I [arXiv:2410.14647]
-
Anna Biggs, Aidan Herderschee: Higher-point correlators in the BFSS matrix model [arXiv:2503.14685]
Discussion as a solution to the open problem of defining M-theory is in
- Gregory Moore, section 12, p. 43-44 in: Physical Mathematics and the Future, talk at Strings 2014 [talk slides, companion text pdf, pdf]
where it says:
A good start was given by the Matrix theory approach of Banks, Fischler, Shenker and Susskind. We have every reason to expect that this theory produces the correct scattering amplitudes of modes in the 11-dimensional supergravity multiplet in 11-dimensional Minkowski space - even at energies sufficiently large that black holes should be created. (This latter phenomenon has never been explicitly demonstrated). But Matrix theory is only a beginning and does not give us the whole picture of M-theory. The program ran into increasing technical difficulties when more complicated compactifications were investigated. (For example, compactification on a six-dimensional torus is not very well understood at all. ). Moreover, to my mind, as it has thus far been practiced it has an important flaw: It has not led to much significant new mathematics.
If history is a good guide, then we should expect that anything as profound and far-reaching as a fully satisfactory formulation of M-theory is surely going to lead to new and novel mathematics. Regrettably, it is a problem the community seems to have put aside - temporarily. But, ultimately, Physical Mathematics must return to this grand issue.
Derivation from open string field theory is discussed in
- Taejin Lee, Covariant Open String Field Theory on Multiple D-Branes (arXiv:1703.06402)
Relation to the 6d (2,0)-supersymmetric QFT:
- Micha Berkooz, Moshe Rozali, Nathan Seiberg, Matrix Description of M-theory on and (arXiv:hep-th/9704089)
Quantization of the M2-brane sigma-model to a matrix model
The Poisson bracket-formulation of the classical light-cone gauge Hamiltonian for the bosonic relativistic membrane and the corresponding matrix commutator regularization is due to:
- Jens Hoppe, Quantum theory of a massless relativistic surface and a two-dimensional bound state problem, MIT 1982 (dspace:1721.1/15717, pdf)
Some exact solutions:
-
Jens Hoppe, Exact algebraic M(em)brane solutions arXiv:2107.00569
-
Jens Hoppe, The fast non-commutative sharp drop arXiv:2302.13146
On the regularized light-cone gauge quantization of the Green-Schwarz sigma model for the M2-brane on (super) Minkowski spacetime, yielding the BFSS matrix model:
Original articles:
- Bernard de Wit, Jens Hoppe, Hermann Nicolai, On the Quantum Mechanics of Supermembranes, Nucl. Phys. B 305 (1988) 545-581 [doi:10.1016/0550-3213(88)90116-2, spire:261702, pdf, pdf]
Observation that the spectrum is continuous:
- Bernard de Wit, W. Lüscher, Hermann Nicolai, The supermembrane is unstable, Nucl. Phys. B 320 (1989) 135 [doi:10.1016/0550-3213(89)90214-9, spire:266584]
Review:
-
Hermann Nicolai, Robert C. Helling, Supermembranes and M(atrix) Theory, In: Trieste 1998, Nonperturbative aspects of strings, branes and supersymmetry (1998) 29-74 (arXiv:hep-th/9809103, spire:476366)
-
Jens Hoppe, Membranes and Matrix Models [arXiv:hep-th/0206192]
-
Arundhati Dasgupta, Hermann Nicolai, Jan Plefka, An Introduction to the Quantum Supermembrane, Grav. Cosmol. 8 1 (2002) and Rev. Mex. Fis. 49S1 (2003) 1-10 [arXiv:hep-th/0201182, spire:582067]
-
Gijs van den Oord, On Matrix Regularisation of Supermembranes MSc thesis (2006) (pdf)
-
Meer Ashwinkumar, Lennart Schmidt, Meng-Chwan Tan, Section 2 of: Matrix Regularization of Classical Nambu Brackets and Super -Branes (arXiv:2103.06666)
The generalization to pp-wave spacetimes (leading to the BMN matrix model):
-
Keshav Dasgupta, Mohammad Sheikh-Jabbari, Mark Van Raamsdonk, Section 2 of: Matrix Perturbation Theory For M-theory On a PP-Wave, JHEP 0205:056, 2002 (arXiv:hep-th/0205185)
-
Keshav Dasgupta, Mohammad Sheikh-Jabbari, Mark Van Raamsdonk, Section 2 of: Matrix Perturbation Theory For M-theory On a PP-Wave, JHEP 0205:056, 2002 (arXiv:hep-th/0205185)
See also
-
Mike Duff, T. Inami, Christopher Pope, Ergin Sezgin, Kellogg Stelle, Semiclassical Quantization of the Supermembrane, Nucl.Phys. B297 (1988) 515-538 (spire:247064)
-
Daniel Kabat, Washington Taylor, section 2 of: Spherical membranes in Matrix theory, Adv. Theor. Math. Phys. 2: 181-206, 1998 (arXiv:hep-th/9711078)
-
Nathan Berkovits, Towards Covariant Quantization of the Supermembrane (arXiv:hep-th/0201151)
-
Qiang Jia, On matrix description of D-branes (arXiv:1907.00142)
A new kind of perturbation series for the quantized super-membrane:
- Olaf Lechtenfeld, Hermann Nicolai, A perturbative expansion scheme for supermembrane and matrix theory (arXiv:2109.00346)
Relation to the string dilaton under double dimensional reduction:
- Krzysztof A. Meissner, Hermann Nicolai, Fundamental Membranes and the String Dilaton, J. High Energ. Phys. 2022 219 (2022) arXiv:2208.05822, doi:10.1007/JHEP09(2022)219
See also in relation to the ABJM model:
- Asadig Mohammed, Jeff Murugan, Horatiu Nastase, Looking for a Matrix model of ABJM, Phys. Rev. D82:086004, 2010 (arXiv:1003.2599)
Relation to M5-branes
Discussion of light cone longitudal M5-branes in the BFSS matrix model (for light cone transversal M5-s see at BMN matrix model):
-
Tom Banks, Nathan Seiberg, Stephen Shenker, Branes from Matrices, Nucl. Phys. B490:91-106, 1997 (arXiv:hep-th/9612157)
-
Judith Castelino, Sangmin Lee, Washington Taylor, Longitudinal 5-branes as 4-spheres in Matrix theory, Nucl. Phys. B526:334-350, 1998 (arXiv:hep-th/9712105)
(introducing the fuzzy 4-sphere)
Discussion of a BFSS-like matrix model for MK6-branes:
- Amihay Hanany, Gilad Lifschytz, M(atrix) Theory on and a m(atrix) Theory Description of KK Monopoles, Nucl. Phys. B519:195-213, 1998 (arXiv:hep-th/9708037)
Ground state problem
There remains the problem of existence of a sensible ground state of the BFSS model.
- Bernard de Wit, M. Luscher, Hermann Nicolai, The Supermembrane Is Unstable, Nucl.Phys. B320 (1989) 135-159 (spire:266584, doi:10.1016/0550-3213(89)90214-9)
For a new attempt at solving this problem, and for pointers to previous attempts see
-
L. Boulton, M.P. Garcia del Moral, A. Restuccia, The ground state of the D=11 supermembrane and matrix models on compact regions, Nuclear Physics B Volume 910, September 2016, Pages 665-684 (arXiv:1504.04071)
-
L. Boulton, M.P. Garcia del Moral, A. Restuccia, Measure of the potential valleys of the supermembrane theory, Physics Letters B Volume 797, 2019, 134873 (arXiv:1811.05758)
Graviton scattering
Computation of graviton scattering amplitudes with the BFSS matrix model:
-
Katrin Becker, Melanie Becker, A Two-Loop Test of M(atrix) Theory, Nucl.Phys. B506 (1997) 48-60 (arXiv:hep-th/9705091)
-
Katrin Becker, Melanie Becker, Joseph Polchinski, Arkady Tseytlin, Higher Order Graviton Scattering in M(atrix) Theory, Phys. Rev. D 56 (1997) 3174-3178 [arXiv:hep-th/9706072, doi:10.1103/PhysRevD.56.R3174]
-
also Kabat-Taylor 97
-
M. Fabbrichesi, Graviton scattering in matrix theory and supergravity, in: Ceresole A., Kounnas C., Dieter Lüst, Stefan Theisen (eds.) Quantum Aspects of Gauge Theories, Supersymmetry and Unification, Lecture Notes in Physics, vol 525. Springer, Berlin, Heidelberg (arXiv:hep-th/9811204)
-
Robert Helling, Jan Plefka, Marco Serone, Andrew Waldron, Three-graviton scattering in M-theory, Nuclear Physics B 559 1–2 (1999) 184-204 [arXiv:hep-th/9905183, doi:10.1016/S0550-3213(99)00451-4]
-
Robert Echols, M-theory, supergravity and the matrix model: Graviton scattering and non-renormalization theorems, PhD thesis, 1999 [pdf]
-
Aidan Herderschee, Juan Maldacena, Three Point Amplitudes in Matrix Theory [arXiv:2312.12592]
-
Juan Maldacena, Three point amplitudes + Soft theorems in the BFSS matrix model, talk at KITP Conference: Spacetime and String Theory (Apr 2024) [doi;10.26081/K62T48]
In relation to the soft graviton theorem:
-
Noah Miller, Andrew Strominger, Adam Tropper, Tianli Wang, Soft Gravitons in the BFSS Matrix Model [arXiv:2208.14547]
-
Adam Tropper, Tianli Wang, Lorentz Symmetry and IR Structure of The BFSS Matrix Model [arXiv:2303.14200]
-
Aidan Herderschee, Juan Maldacena, Soft Theorems in Matrix Theory [arXiv:2312.15111]
Black holes
Relation to black holes in string theory:
-
Tom Banks, Willy Fischler, Igor Klebanov, Leonard Susskind, Schwarzschild Black Holes from Matrix Theory, Phys.Rev.Lett.80:226-229,1998 (arXiv:hep-th/9709091)
-
Tom Banks, Willy Fischler, Igor Klebanov, Leonard Susskind, Schwarzchild Black Holes in Matrix Theory II, JHEP 9801:008,1998 (arXiv:hep-th/9711005)
-
Igor Klebanov, Leonard Susskind, Schwarzschild Black Holes in Various Dimensions from Matrix Theory, Phys.Lett.B416:62-66,1998 (arXiv:hep-th/9709108)
-
Edi Halyo, Six Dimensional Schwarzschild Black Holes in M(atrix) Theory (arXiv:hep-th/9709225)
-
Gary Horowitz, Emil Martinec, Comments on Black Holes in Matrix Theory, Phys. Rev. D 57, 4935 (1998) (arXiv:hep-th/9710217)
-
Daniel Kabat, Washington Taylor, Spherical membranes in Matrix theory, Adv.Theor.Math.Phys.2:181-206,1998 (arXiv:hep-th/9711078)
-
Yoshifumi Hyakutake, Black Hole and Fuzzy Objects in BFSS Matrix Model [arXiv:1801.07869]
-
Haoxing Du, Vatche Sahakian, Emergent geometry from stochastic dynamics, or Hawking evaporation in M(atrix) theory (arXiv:1812.05020)
(combination with random matrix theory)
-
Oscar J. C. Dias, Jorge E. Santos: The Low Energy Limit of BFSS Quantum Mechanics [arXiv:2407.15921]
-
Angshuman Choudhury, Davide Laurenzano: Entanglement Entropy for the Black 0-Brane [arXiv:2407.13336]
Relation to lattice gauge theory
Relation to lattice gauge theory and numerical tests of AdS/CFT:
-
Anosh Joseph, Review of Lattice Supersymmetry and Gauge-Gravity Duality (arXiv:1509.01440)
-
Veselin G. Filev, Denjoe O’Connor, The BFSS model on the lattice, JHEP 1605 (2016) 167 (arXiv:1506.01366)
-
Masanori Hanada, What lattice theorists can do for superstring/M-theory, International Journal of Modern Physics AVol. 31, No. 22, 1643006 (2016) (arXiv:1604.05421)
-
Georg Bergner, Norbert Bodendorfer, Masanori Hanada, Stratos Pateloudis, Enrico Rinaldi, Andreas Schäfer, Pavlos Vranas, Hiromasa Watanabe, Confinement/deconfinement transition in the D0-brane matrix model – A signature of M-theory?, JHEP 05 (2022) 096 [arXiv:2110.01312]
Holography
On AdS/CFT in the form of AdS2/CFT1 with the BFSS matrix model on the CFT side and black hole-like solutions in type IIA supergravity on the AdS side:
-
Juan Maldacena, Alexey Milekhin, To gauge or not to gauge?, JHEP 04 (2018) 084 (arxiv:1802.00428)
-
Alfred Bovon, Henning Samtleben, Dimitrios Tsimpis: Holographic deformations of matrix models [arXiv:2503.15954]
and concerning the analog of its holographic entanglement entropy:
- Tarek Anous, Joanna L. Karczmarek, Eric Mintun, Mark Van Raamsdonk, Benson Way, Areas and entropies in BFSS/gravity duality (arXiv:1911.11145)
See also:
- Chris D. A. Blair, Johannes Lahnsteiner, Niels A. Obers, Ziqi Yan: Matrix Theory Reloaded: A BPS Road to Holography [arXiv:2410.03591]
Cosmology
On non-perturbative string theoretic cosmology (and the Brandenberger-Vafa mechanism) via the BFSS/IKKT matrix model:
-
Suddhasattwa Brahma, Robert Brandenberger, Samuel Laliberte: Emergent Cosmology from Matrix Theory, J. High Energ. Phys. 2022 67 (2022) [arXiv:2107.11512, doi:10.1007/JHEP03(2022)067]
-
Suddhasattwa Brahma, Robert Brandenberger, Samuel Laliberte: Emergent Early Universe Cosmology from BFSS Matrix Theory, International Journal of Modern Physics D 31 14 (2022) 2242004 [arXiv:2205.06016, doi:10.1142/S0218271822420044]
-
Suddhasattwa Brahma, Robert Brandenberger, Samuel Laliberte: Emergent Metric Space-Time from Matrix Theory, J. High Energ. Phys. 2022 31 (2022) [arXiv:2206.12468, doi:10.1007/JHEP09(2022)031]
-
Suddhasattwa Brahma, Robert Brandenberger, Samuel Laliberte: BFSS Matrix Model Cosmology: Progress and Challenges, Physics 5 1 (2023) [arXiv:2210.07288, doi:10.3390/physics5010001]
-
Robert Brandenberger: Emergent Metric Space-Time from the BFSS Matrix Model, talk at Perimeter Institute (May 2023) [doi:10.48660/23050109, video:pirsa:23050109, slides:pdf]
-
Robert Brandenberger, Julia Pasiecznik: On the Origin of the Symmetry Breaking in the IKKT Matrix Model [arXiv:2409.00254, spire:2824186]
See also at IKKT matrix model – References – Computer simulation.
Last revised on March 21, 2025 at 08:50:49. See the history of this page for a list of all contributions to it.