nLab Hopf invariant
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Definition
In ordinary cohomology
For with , consider continuous functions between spheres of the form
The homotopy cofiber of (the attaching space induced by )
Hence for generators of the cohomology groups in degree and (unique up to choice of sign), respectively, there exists an integer which expresses the cup product square of as a multiple of :
This integer is called the Hopf invariant of (e.g. Mosher-Tangora 86, p. 33).
This depends on the choices made only up to sign. In particular it has a well-defined mod-2 reduction image (in Z/2), and as such it is the Steenrod square
In generalized cohomology
Here is a more abstract picture of the Hopf invariant in abstract homotopy theory (following SS21):
Let be a multiplicative cohomology theory, assumed to vanish in degree
We write for its classifying spaces, hence for the component spaces of its representing spectrum.
(For the case of ordinary cohomology we have an Eilenberg-MacLane space.)
Now let
be a map (1). Then its -Hopf invariant “is” the following homotopy pasting diagram of pointed homotopy types (see also at e-invariant is Todd class of cobounding (U,fr)-manifold):
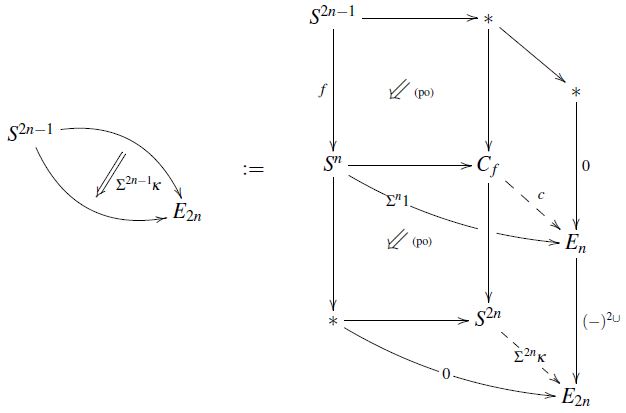
-
the top square is defined to be a homotopy pushout, exhibiting the attaching space ;
-
the total rectangle is defined to be a homotopy pushout, exhibiting the suspension of to ;
-
the bottom square is hence a homotopy pushout by the pasting law;
-
by assumption (3) the restriction of to trivializes, exhibited by a choice of homotopy filling the full top part of the diagram; and by the universal property of the top homotopy-pushout this corresponds equivalently to the dashed morphism ;
-
the restriction of the cup square cohomology operation on to trivializes: factors through the component space of the connective cover , whence its cup square (by the discussion at connective cover – For ring spectra) factors through the -connective th component space of the same connective cover (as in a standard argument in complex oriented cohomology theory, e.g. Lurie, Lec. 4. Exmpl. 8, or see Conner-Floyd 66, Part I, Cor. 7.2):
-
This yields the homotopy filling the full bottom part of the diagram above; and by the universal property of the bottom homotopy-pushout this corresponds equivalently to a dashed morphism , labeled by some class
-
finally, by the homotopy-pushout property of the total rectangle, this class also labels the total homotopy filling the full diagram.
We see that:
-
for being ordinary cohomology, is the traditional Hopf invariant as discussed above;
-
for being complex topological K-theory, is the Hopf invariant in K-theory as used in Adams-Atiyah 66.
In the case that the map is one the classical Hopf fibrations, the attaching space above is a projective space (by the discussion at cell structure of projective spaces) and the choice of homotopy is the choice of an orientation in -cohomology theory to second stage. Specifically:
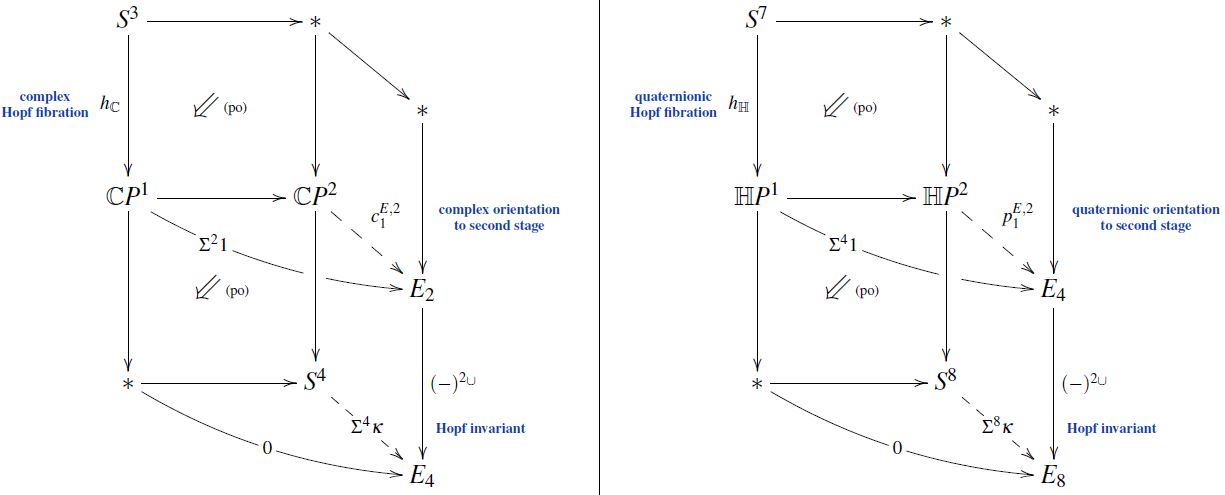
-
for the complex Hopf fibration the attaching space is complex projective space and the choice of homotopy is a choice of complex orientation to second stage;
-
for the quaternionic Hopf fibration the attaching space is quaternionic projective space and the choice of homotopy is a choice of quaternionic orientation to second stage.
Moreover, the de-composition of this pasting diagram exhibits the homotopy Whitehead integral/functional cup product-formula for the Hopf invariant:
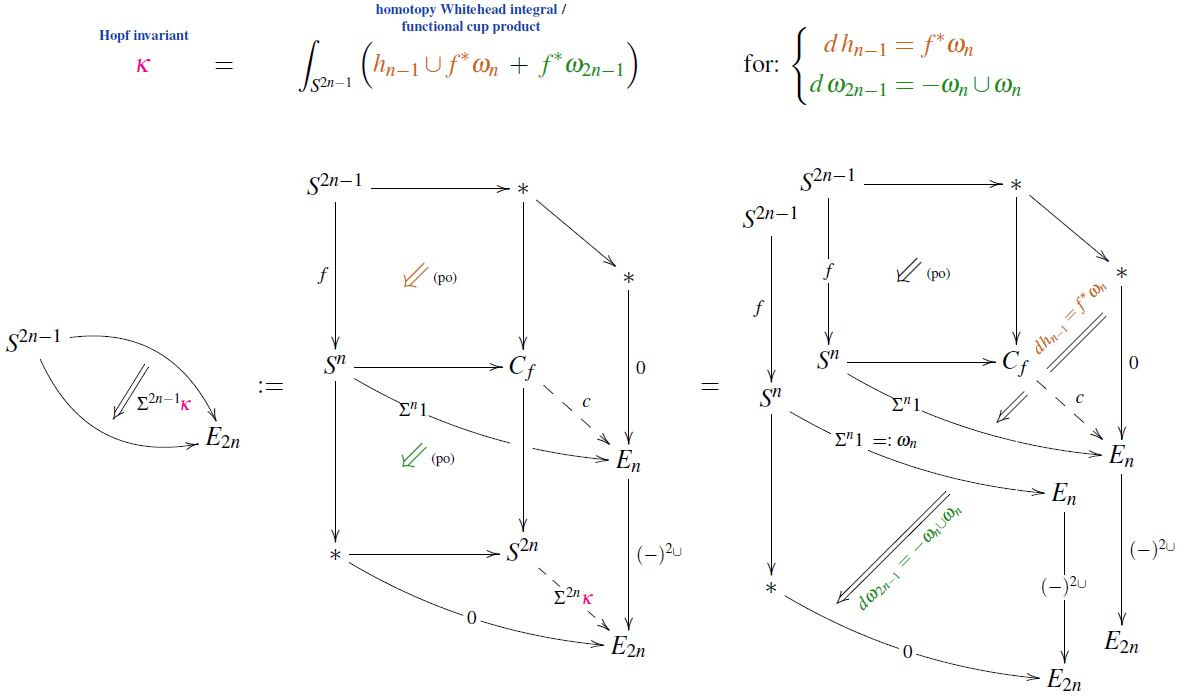
Properties
Generic values
For odd, the Hopf invariant necessarily vanishes. For even however, then there is a homomorphism
whose image contains at least the even integers.
Hopf invariant one
A famous open question in the 1950s was which maps (1) have Hopf invariant one, namely (2).
The Hopf invariant one theorem (Adams60) states that the only maps of Hopf invariant one, , are the Hopf constructions on the four real normed division algebras:
-
the real Hopf fibration;
Via Sullivan models
Proposition
By standard results in rational homotopy theory, every continuous function
corresponds to a unique dgc-algebra homomorphism
between Sullivan models of n-spheres.
The unique free coefficient of this homomorphism is the Hopf invariant of :
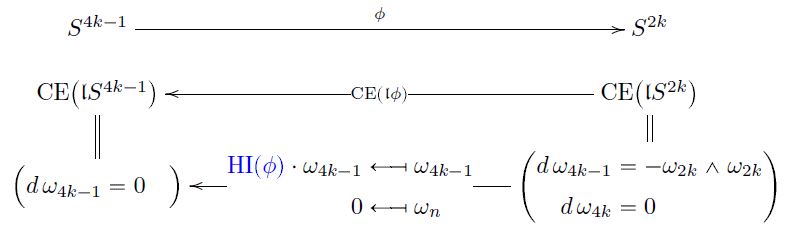
Whitehead integral formula
See at Whitehead integral formula and see the references below
Related concepts
References
General
-
Dale Husemöller, chapter 15 of: Fibre Bundles, Graduate Texts in Mathematics 20, Springer New York (1966) (doi:10.1007/978-1-4757-2261-1)
-
Robert Mosher, Martin Tangora, p. 33 of Cohomology operations and applications in homotopy theory, Harper & Row 1986 (pdf)
-
Michael Crabb, Andrew Ranicki, The Geometric Hopf Invariant and Surgery Theory, Springer Monographs in Mathematics, Springer (2017) doi:10.1007/978-3-319-71306-9, slides pdf, pdf
(in relation to surgery theory)
-
Klaus Wirthmüller, section 12 of: Vector bundles and K-theory, 2012 (pdf)
-
Gereon Quick, The Hopf invariant one problem via K-theory, lecture notes in: Advanced algebraic topology, 2014 (pdf)
See also:
- Wikipedia, Hopf invariant
And see the references at Hopf invariant one for more, in particular for the formulation via topological K-theory.
Whitehead’s integral formula
Discussion via differential forms/real homotopy theory/rational homotopy theory (see also at functional cup product):
-
J. H. C. Whitehead, An expression of Hopf’s invariant as an integral, Proc. Nat. Acad. Sci. USA 33 (1947), 117–123 (jstor:87688)
-
Hassler Whitney, Section 31 in Geometric Integration Theory, 1957 (pup:3151)
-
André Haefliger, p. 3 of Whitehead products and differential forms, In: P.A. Schweitzer (ed.), Differential Topology, Foliations and Gelfand-Fuks Cohomology, Lecture Notes in Mathematics, vol 652. Springer 1978 (doi:10.1007/BFb0063500)
-
Raoul Bott, Loring Tu, Prop. 17.22 in Differential Forms in Algebraic Topology, Graduate Texts in Mathematics 82, Springer 1982 (doi:10.1007/BFb0063500)
-
Lee Rudolph, Whitehead’s Integral Formula, Isolated Critical Points, and the Enhancement of the Milnor Number, Pure and Applied Mathematics Quarterly Volume 6, Number 2, 2010 (arXiv:0912.4974)
-
Phillip Griffiths, John Morgan, Section 14.5 of: Rational Homotopy Theory and Differential Forms, Progress in Mathematics Volume 16, Birkhauser (1981, 2013) (doi:10.1007/978-1-4614-8468-4)
-
Dev Sinha, Ben Walter, Lie coalgebras and rational homotopy theory II: Hopf invariants, Trans. Amer. Math. Soc. 365 (2013), 861-883 (arXiv:0809.5084, doi:10.1090/S0002-9947-2012-05654-6)
-
Felix Wierstra, Hopf Invariants in Real and Rational Homotopy Theory (2017) [diva:146246, pdf]
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M5 WZ term level quantization, Comm. Math. Phys. 2020 (arXiv:1906.07417)
Last revised on April 3, 2023 at 11:11:29. See the history of this page for a list of all contributions to it.