nLab suspension
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
In point-set topology
In point-set topology, the (un-reduced) suspension of an inhabited topological space is the quotient space of the cylinder space (the product space with a closed interval) by the relation which identifies all the points at either end:
The following graphics gives an artistic impression of the suspension of a (non-empty) space , indicated in gray:
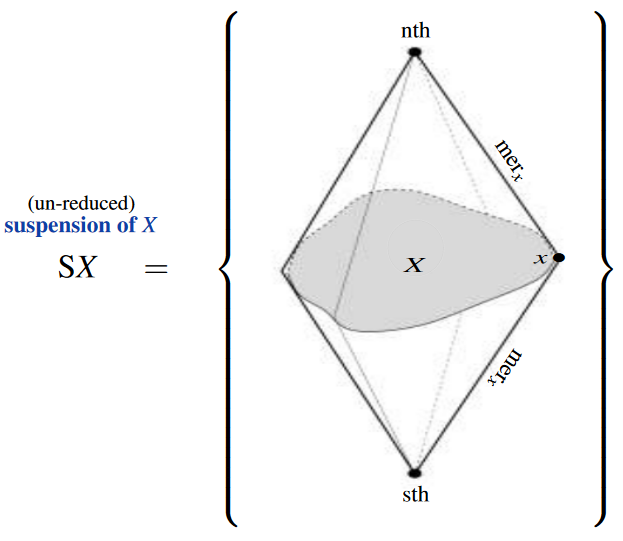
(adapted from Muro 2010)
In particular, the suspension of an -sphere is homeomorphic to the -sphere
namely the union of (in terms of the above graphics):
Hence, by induction, the -sphere is homeomorphic to the -fold suspension of the 0-sphere:
In homotopy theory
Regarded in the classical homotopy category, the suspension construction (1) on a CW-complex is a canonical model for the suspension object of the homotopy type represented by — namely the homotopy pushout of the terminal map along itself) — and as such plays a key role in homotopy theory and stable homotopy theory.
This also explains the usual definition of the suspension of the empty space as the 0-sphere
since the latter does model the homotopy pushout of along itself (which is just a 1-categorytheoretic pushout and hence the coproduct of the point space with itself).
For more on this see at suspension object.
More precisely, what appears in most of algebraic topology and stable homotopy theory is the reduced suspension of pointed topological spaces (and eventually their suspension spectra):
where in addition the copy of the interval over the given basepoint is identified with a single point. For CW-complexes the reduced suspension is weakly homotopy equivalent to the ordinary suspension.
In this context of (stable) homotopy theory, the suspension construction is part of the canonical point-set model for cofiber sequences induced from any mapping cone construction:
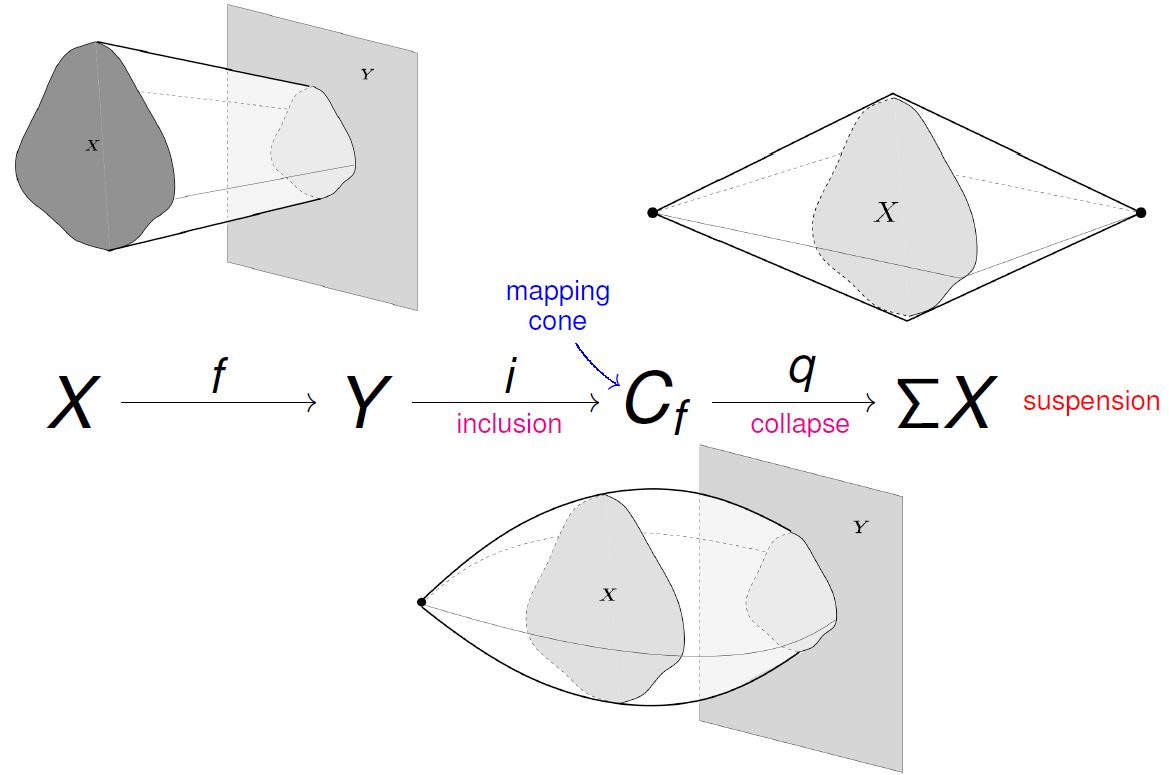
(from Muro 2010)
Definitions
Let be a space (such as a topological space, or something more interesting like a generalized smooth space). Let be the unit interval in the real line; let be the -point discrete space . Let be the cartesian product of , , and ; let be the disjoint union of , and . We will suppress reference to the inclusion maps into ; it will be clear from context how to parse an element of the latter.
Generalisable definition
The suspension of is the quotient space of by the equivalence relation generated by:
- for in ;
- for in ;
- for in ;
- for in .
Generalisation: the join
This generalises immediately to an operation called the join of two spaces and ; this is the quotient space of by the equivalence relation generated by:
- for in and in ;
- for in and in .
(Compare join of simplicial sets and join of topological spaces, the same operation in another guise.) Then we have .
Simplified definition
It is somewhat simpler to define as the quotient space of by the equivalence relation generated by:
- for in ;
- for in .
This works to define a topological space, but it does not directly give the smooth structure that matches the picture above.
Further simplified for pointed spaces
If has a point , hence if it is inhabited, then we can define as the quotient space of by the equivalence relation generated by:
- for in ;
- for in .
This is probably the most common definition seen, but it only works for an inhabited space (and even then gives only the topological structure).
Reduced suspension
To make the suspension of a pointed space again a pointed space one may further collapse in the set to the point. The result then is called the reduced suspension of and is denoted
Properties
As a functor
It's easy to extend the suspension operation to a functor from Top to itself.
Relation between suspension and reduced suspension
For CW-complexes suspension and reduced suspension agree, up to weak homotopy equivalence.
Cogroup structure
In the pointed case (reduced suspension): suspensions are H-cogroup objects
Examples
Suspension of cubes
The suspension of the -cube is the -cube, probably best visualised as a diamond. This gives a recursive definition of cube, starting with the -cube as the point, which is not the suspension of anything. Note that this not only gives us the topological structure of the cube, but also (by working in an appropriate category of smooth spaces throughout) the correct smooth structure on the cube as a manifold with corners. You can probably even get the correct metric on the cube (normalised to have diagonals of length ) automatically by using a more complicated quotienting process.
Suspension of spheres
Up to homeomorphism, the suspension of the -sphere is the -sphere, and the reduced suspension is
See at one-point compactification – Examples – Spheres for details.
Notice that the -sphere is (topologically) the boundary of the -cube. The coincidence that ‘sphere’ and ‘suspension’ both begin with ‘s’ has not been ignored; we can write , where on the left is the -sphere and on the right is the -fold composite of the suspension functor. (Actually, you should start with the -sphere as the empty space, which is not the suspension of anything; then the -sphere is .) However, this does not give the correct smooth structure on the sphere, unless perhaps there is some more sophisticated definition that fixes this (but then that would break the cube). It might be more appropriate to say that the suspension of the -globe is the -globe.
Suspension of simplices
Up to topological structure, the suspension of the -simplex is the -simplex, but now this is not very useful. To study simplices, you should use the cone functor instead, which is , where is the point.
Related concepts
References
For discussion of reduced suspension see there. For more general discussion of homotopy pushouts see also there. Most introductions to homotopy theory discuss suspension, in one form or other, see there.
Textbook accounts with the basics definition:
-
Klaus Jänich, p. 41 in: Topology, Undergraduate Texts in Mathematics, Springer (1984, 1999) [ISBN:9780387908922, doi:10.1007/978-3-662-10574-0, Chapters 1-2: pdf]
-
Allen Hatcher, p. 8 in: Algebraic Topology, Cambridge University Press (2002) [ISBN:9780521795401, webpage]
A textbook which knows that the suspension of the empty set is the 0-sphere (although even it regards this as an exception):
- Anatole Katok, Alexey Sossinsky, Chapter 1 of: Introduction to Modern Topology and Geometry (2010) [toc pdf, pdf]
Discussion of the suspension type as a higher inductive type in homotopy type theory:
- Univalent Foundations Project, §6.5 in: Homotopy Type Theory – Univalent Foundations of Mathematics (2013) [web, pdf]
On the free loop space of a suspension:
- Ralph Cohen, A model for the free loop space of a suspension Lecture Notes in Mathematics, 1987, Volume 1286/1987, 193-207
On the question on what is the Eckmann-Hilton dual to :
- D. B. Fuks, Eckmann–Hilton duality and the theory of functors in the category of topological spaces, 1966 Russ. Math. Surv. 21 1–33 doi, free Russian original pdf
The above graphics is taken from
- Fernando Muro, Representability of Cohomology Theories, Joint Mathematical Conference CSASC 2010, 22–27 January 2010, Prague, Czech Republic [slides, pdf]
Last revised on October 12, 2023 at 05:41:00. See the history of this page for a list of all contributions to it.