nLab classical model structure on simplicial sets
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Model category theory
model category, model -category
Definitions
Morphisms
Universal constructions
Refinements
Producing new model structures
Presentation of -categories
Model structures
for -groupoids
-
on chain complexes/model structure on cosimplicial abelian groups
related by the Dold-Kan correspondence
for equivariant -groupoids
for rational -groupoids
for rational equivariant -groupoids
for -groupoids
for -groups
for -algebras
general -algebras
specific -algebras
for stable/spectrum objects
for -categories
for stable -categories
for -operads
for -categories
for -sheaves / -stacks
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
The classical model structure on simplicial sets or Kan-Quillen model structure , (Quillen 67, II.3) is a model category structure on the category sSet of simplicial sets which represents the standard classical homotopy theory.
Its weak equivalences are the simplicial weak equivalences (isomorphisms on simplicial homotopy groups), its fibrations are the Kan fibrations and its cofibrations are the monomorphisms (degreewise injections).
The singular simplicial complex/geometric realization adjunction constitutes a Quillen equivalence between and , the classical model structure on topological spaces. This is sometimes called part of the statement of the homotopy hypothesis for Kan complexes. In the language of (∞,1)-category theory this means that and both are presentations of the (∞,1)-category ∞Grpd of ∞-groupoids.
There are also other model structures on sSet itself, see at model structure on simplicial sets for more. This entry here focuses on just the standard classical model structure.
Background on combinatorial topology
This section reviews basics of the theory of simplicial sets (the modern version of the original “combinatorial topology”) necessary to define, verify and analyse the classical model category structure on simplicial sets, below. See also at simplicial homotopy theory.
Simplicial sets
The concept of simplicial sets is secretly well familiar already in basic algebraic topology: it reflects just the abstract structure carried by the singular simplicial complexes of topological spaces, as in the definition of singular homology and singular cohomology.
Conversely, every simplicial set may be geometrically realized as a topological space. These two adjoint operations turn out to exhibit the homotopy theory of simplicial sets as being equivalent (Quillen equivalent) to the homotopy theory of topological spaces. For some purposes, working in simplicial homotopy theory is preferable over working with topological homotopy theory.
Definition
For , the topological n-simplex is, up to homeomorphism, the topological space whose underlying set is the subset
of the Cartesian space , and whose topology is the subspace topology induces from the canonical topology in .
Example
For this is the point, .
For this is the standard interval object .
For this is the filled triangle.
For this is the filled tetrahedron.
Definition
For , and , the th -face (inclusion) of the topological -simplex, def. , is the subspace inclusion
induced under the coordinate presentation of def. , by the inclusion
which “omits” the th canonical coordinate:
Example
The inclusion
is the inclusion
of the “right” end of the standard interval. The other inclusion
is that of the “left” end .
(graphics taken from Friedman 08)
Definition
For and the th degenerate -simplex (projection) is the surjective map
induced under the barycentric coordinates of def. under the surjection
which sends
Definition
For Top and , a singular -simplex in is a continuous map
from the topological -simplex, def. , to .
Write
for the set of singular -simplices of .
(graphics taken from Friedman 08)
The sets here are closely related by an interlocking system of maps that make them form what is called a simplicial set, and as such the collection of these sets of singular simplices is called the singular simplicial complex of . We discuss the definition of simplicial sets now and then come back to this below in def. .
Since the topological -simplices from def. sit inside each other by the face inclusions of def.
and project onto each other by the degeneracy maps, def.
we dually have functions
that send each singular -simplex to its -face and functions
that regard an -simplex as beign a degenerate (“thin”) -simplex. All these sets of simplices and face and degeneracy maps between them form the following structure.
Definition
A simplicial set is
-
for each injective map of totally ordered sets
a function – the th face map on -simplices;
-
for each surjective map of totally ordered sets
a function – the th degeneracy map on -simplices;
such that these functions satisfy the simplicial identities.
Definition
The simplicial identities satisfied by face and degeneracy maps as above are (whenever these maps are composable as indicated):
-
if ,
-
if .
It is straightforward to check by explicit inspection that the evident injection and restriction maps between the sets of singular simplices make into a simplicial set. However for working with this, it is good to streamline a little:
Definition
The simplex category is the full subcategory of Cat on the free categories of the form
Remark
This is called the “simplex category” because we are to think of the object as being the “spine” of the -simplex. For instance for we think of as the “spine” of the triangle. This becomes clear if we don’t just draw the morphisms that generate the category , but draw also all their composites. For instance for we have_
Proposition
A functor
from the opposite category of the simplex category to the category Set of sets is canonically identified with a simplicial set, def. .
Proof
One checks by inspection that the simplicial identities characterize precisely the behaviour of the morphisms in and .
This makes the following evident:
Example
The topological simplices from def. arrange into a cosimplicial object in Top, namely a functor
With this now the structure of a simplicial set on , def. , is manifest: it is just the nerve of with respect to , namely:
Definition
For a topological space its simplicial set of singular simplicies (often called the singular simplicial complex)
is given by composition of the functor from example with the hom functor of Top:
Remark
It turns out – this is the content of the homotopy hypothesis-theorem (Quillen 67) – that homotopy type of the topological space is entirely captured by its singular simplicial complex . Moreover, the geometric realization of is a model for the same homotopy type as that of , but with the special property that it is canonically a cell complex – a CW-complex. Better yet, is itself already good cell complex, namely a Kan complex. We come to this below.
Simplicial homotopy
The concept of homotopy of morphisms between simplicial sets proceeds in direct analogy with that in topological spaces.
Definition
For a simplicial set, def. , its simplicial cylinder object is the Cartesian product (formed in the category sSet).
between two morphisms
of simplicial sets is a morphism
such that the following diagram commutes
For a Kan complex, def. , its simplicial path space object is the function complex (formed in the category sSet).
between two morphisms
of simplicial sets is a morphism
such that the following diagram commutes
Proposition
For a Kan complex, def. , and any simplicial set, then left homotopy, def. , regarded as a relation
on the hom set , is an equivalence relation.
Definition
A morphism of simplicial sets is a left/right homotopy equivalence if there exists a morphisms and left/right homotopies (def. )
The the basic invariants of simplicial sets/Kan complexes in simplicial homotopy theory are their simplicial homotopy groups, to which we turn now.
Given that a Kan complex is a special simplicial set that behaves like a combinatorial model for a topological space, the simplicial homotopy groups of a Kan complex are accordingly the combinatorial analog of the homotopy groups of topological spaces: instead of being maps from topological spheres modulo maps from topological disks, they are maps from the boundary of a simplex modulo those from the simplex itself.
Accordingly, the definition of the discussion of simplicial homotopy groups is essentially literally the same as that of homotopy groups of topological spaces. One technical difference is for instance that the definition of the group structure is slightly more non-immediate for simplicial homotopy groups than for topological homotopy groups (see below).
Definition
For a Kan complex, then its 0th simplicial homotopy group (or set of connected components) is the set of equivalence classes of vertices modulo the equivalence relation
For a vertex and for , , then the underlying set of the th simplicial homotopy group of at – denoted – is, the set of equivalence classes of morphisms
from the simplicial -simplex to , such that these take the boundary of the simplex to , i.e. such that they fit into a commuting diagram in sSet of the form
where two such maps are taken to be equivalent is they are related by a simplicial homotopy
that fixes the boundary in that it fits into a commuting diagram in sSet of the form
These sets are taken to be equipped with the following group structure.
Definition
For a Kan complex, for , for and for two representatives of as in def. , consider the following -simplices in :
This corresponds to a morphism from a horn of the -simplex into . By the Kan complex property of this morphism has an extension through the -simplex
From the simplicial identities one finds that the boundary of the -simplex arising as the th boundary piece of is constant on
So represents an element in and we define a product operation on by
(e.g. Goerss-Jardine 99, p. 26)
Remark
All the degenerate -simplices in def. are just there so that the gluing of the two -cells and to each other can be regarded as forming the boundary of an -simplex except for one face. By the Kan extension property that missing face exists, namely . This is a choice of gluing composite of with .
Lemma
The product on homotopy group elements in def. is well defined, in that it is independent of the choice of representatives , and of the extension .
e.g. (Goerss-Jardine 99, lemma 7.1)
e.g. (Goerss-Jardine 99, theorem 7.2)
Remark
The first homotopy group, , is also called the fundamental group of .
Definition
For two Kan complexes, then a morphism
is called a weak homotopy equivalence if it induces isomorphisms on all simplicial homotopy groups, i.e. if
-
is a bijection of sets;
-
is an isomorphism of groups for all and all ; .
Kan fibrations
Definition
For each , , the -horn is the subsimplicial set
of the simplicial -simplex, which is the union of all faces except the one.
This is called an outer horn if or . Otherwise it is an inner horn.
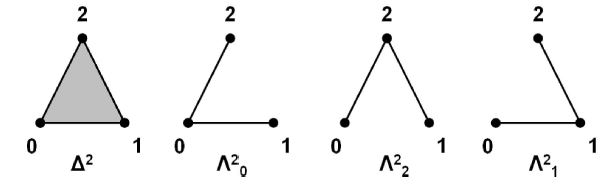
(graphics taken from Friedman 08)
Remark
Since sSet is a presheaf category, unions of subobjects make sense and they are calculated objectwise, thus in this case dimensionwise. This way it becomes clear what the structure of a horn as a functor must therefore be: it takes to the collection of ordinal maps which do not have the element in the image.
Definition
A Kan complex is a simplicial set that satisfies the Kan condition,
-
which says that all horns of the simplicial set have fillers/extend to simplices;
-
which means equivalently that the unique homomorphism from to the point (the terminal simplicial set) is a Kan fibration;
-
which means equivalently that for all diagrams of the form
there exists a diagonal morphism
completing this to a commuting diagram;
-
which in turn means equivalently that the map from -simplices to -horns is an epimorphism
Proposition
For a topological space, its singular simplicial complex , def. , is a Kan complex, def. .
Proof
The inclusions of topological horns into topological simplices are retracts, in that there are continuous maps given by “squashing” a topological -simplex onto parts of its boundary, such that
Therefore the map is an epimorphism, since it is equal to to which has a right inverse .
More generally:
Definition
A morphism in sSet is called a Kan fibration if it has the right lifting property again all horn inclusions, def. , hence if for every commuting diagram of the form
there exists a lift
This is the simplicial incarnation of the concept of Serre fibrations of topological spaces:
Definition
A continuous function between topological spaces is a Serre fibration if for all CW-complexes and for every commuting diagram in Top of the form
there exists a lift
Proposition
A continuous function is a Serre fibration, def. , precisely if (def. ) is a Kan fibration, def. .
The proof uses the basic tool of nerve and realization-adjunction to which we get to below in prop. .
Proof
First observe that the left lifting property against all for a CW-complex is equivalent to left lifting against geometric realization of horn inclusions. Then apply the natural isomorphism , given by the adjunction of prop. and example , to the lifting diagrams.
Lemma
Let be a Kan fibration, def. , and let be two morphisms. If there is a left homotopy (def. ) between these maps, then there is a fiberwise homotopy equivalence, def. , between the pullback fibrations .
(e.g. Goerss-Jardine 99, chapter I, lemma 10.6)
While simplicial sets have the advantage of being purely combinatorial structures, the singular simplicial complex of any given topological space, def. is in general a huge simplicial set which does not lend itself to detailed inspection. The following is about small models.
Definition
A Kan fibration , def. , is called a minimal Kan fibration if for any two cells in the same fiber with the same boundary if they are homotopic relative their boundary, then they are already equal.
More formally, is minimal precisely if for every commuting diagram of the form
then the two composites
are equal.
Proposition
The pullback (in sSet) of a minimal Kan fibration, def. , along any morphism is again a mimimal Kan fibration.
(Goerss-Jardine 99, chapter I, section 4, Joyal-Tierney 09, section 1.7)
Proposition
For every Kan fibration, def. , there exists a fiberwise strong deformation retract to a minimal Kan fibration, def. .
(e.g. Goerss-Jardine 99, chapter I, prop. 10.3, Joyal-Tierney 08, theorem 3.3.1, theorem 3.3.3).
Proof idea
Choose representatives by induction, use that in the induction step one needs lifts of anodyne extensions against a Kan fibration, which exist.
Lemma
A morphism between minimal Kan fibrations, def. , which is fiberwise a homotopy equivalence, def. , is already an isomorphism.
(e.g. Goerss-Jardine 99, chapter I, lemma 10.4)
Proof idea
Show the statement degreewise. In the induction one needs to lift anodyne extensions agains a Kan fibration.
Lemma
Every minimal Kan fibration, def. , over a connected base is a simplicial fiber bundle, locally trivial over every simplex of the base.
(e.g. Goerss-Jardine 99, chapter I, corollary 10.8)
Proof
By assumption of the base being connected, the classifying maps for the fibers over any two vertices are connected by a zig-zag of homotopies, hence by lemma the fibers are connected by homotopy equivalences and then by prop. and lemma they are already isomorphic. Write for this typical fiber.
Moreover, for all the morphisms are left homotopic to and so applying lemma and prop. once more yields that the fiber over each is isomorphic to .
Geometric realization
So far we we have considered passing from topological spaces to simplicial sets by applying the singular simplicial complex functor of def. . Now we discuss a left adjoint of this functor, called geometric realization, which turns a simplicial set into a topological space by identifying each of its abstract n-simplices with the standard topological -simplex.
This is an example of a general abstract phenomenon:
Proposition
Let
be a functor from a small category to a locally small category with all colimits. Then the nerve-functor
has a left adjoint functor , called geometric realization,
given by the coend
(Kan 58)
Example
The singular simplicial complex functor of def. has a left adjoint geometric realization functor
given by the coend
Topological geometric realization takes values in particularly nice topological spaces.
Proposition
The topological geometric realization of simplicial sets in example takes values in CW-complexes.
(e.g. Goerss-Jardine 99, chapter I, prop. 2.3)
Thus for a topological space the adjunction counit of the nerve and realization-adjunction is a candidate for a replacement of by a CW-complex. For this, should be at least a weak homotopy equivalence, i.e. induce isomorphisms on all homotopy groups. Since homotopy groups are built from maps into out of compact topological spaces it is plausible that this works if the topology of is entirely detected by maps out of compact topological spaces into . Topological spaces with this property are called compactly generated.
We take compact topological space to imply Hausdorff topological space.
Definition
A subspace of a topological space is called compactly open or compactly closed, respectively, if for every continuous function out of a compact topological space the preimage is open or closed, respectively.
A topological space is a compactly generated topological space if each of its compactly closed subspaces is already closed.
Write
for the full subcategory of Top on the compactly generated topological spaces.
Often the condition is added that a compactly closed topological space be also a weakly Hausdorff topological space.
Example
Examples of compactly generated topological spaces, def. , include
-
every compact space;
-
every locally compact space;
-
every topological manifold;
-
every CW-complex;
-
every first countable space
Corollary
The topological geometric realization functor of simplicial sets in example takes values in compactly generated topological spaces
Proposition
The subcategory of def. has the following properties
-
It is a coreflective subcategory
The coreflection of a topological space is given by adding to the open subsets of all compactly open subsets, def. .
-
It has all small limits and colimits.
The colimits are computed in , the limits are the image under of the limits as computed in .
-
It is a cartesian closed category.
The cartesian product in is the image under of the Cartesian product formed in .
This is due to (Steenrod 67), expanded on in (Lewis 78, appendix A). One says that prop. with example makes a “convenient category of topological spaces”.
Proposition
Regarded, via corollary as a functor , geometric realization preserves finite limits.
See at Geometric realization is left exact.
Proof idea
The key step in the proof is to use the cartesian closure of (prop. ). This gives that the Cartesian product is a left adjoint and hence preserves colimits in each variable, so that the coend in the definition of the geometric realization may be taken out of Cartesian products.
Lemma
The geometric realization, example , of a minimal Kan fibration, def. is a Serre fibration, def. .
This is due to (Gabriel-Zisman 67). See for instance (Goerss-Jardine 99, chapter I, corollary 10.8, theorem 10.9).
Proof idea
By prop. minimal Kan fibrations are simplicial fiber bundles, locally trivial over each simplex in the base. By prop. this property translates to their geometric realization also being a locally trivial fiber bundle of topological spaces, hence in particular a Serre fibration.
Proposition
The geometric realization, example , of any Kan fibration, def. is a Serre fibration, def. .
This is due to (Quillen 68). See for instance (Goerss-Jardine 99, chapter I, theorem 10.10).
Proposition
For a Kan complex, then the unit of the nerve and realization-adjunction (prop. , example )
is a weak homotopy equivalence, def. .
For any topological space, then the adjunction counit
e.g. (Goerss-Jardine 99, chapter I, prop. 11.1 and p. 63).
Proof idea
Use prop. and prop. applied to the path fibration to proceed by induction.
The classical model structure
Definition
The classical model structure on simplicial sets, , has the following distinguished classes of morphisms:
-
The classical weak equivalences are the simplicial weak equivalences: morphisms whose geometric realization, example , is a weak homotopy equivalence of topological spaces;
-
The classical fibrations are the Kan fibrations, def. ;
-
The classical cofibrations are the monomorphisms of simplicial sets, i.e. the degreewise injections.
Properties
Basic properties
Proposition
In model structure , def. , the following holds.
-
The fibrant objects are precisely the Kan complexes.
-
A morphism of fibrant simplicial sets / Kan complexes is a weak equivalence precisely if it induces an isomorphism on all simplicial homotopy groups, def. .
-
All simplicial sets are cofibrant with respect to this model structure.
Proposition
The acyclic fibrations in , namely the acyclic Kan fibrations (i.e. the maps that are both fibrations as well as weak equivalences) are precisely the morphisms that have the right lifting property with respect to all inclusions of boundaries of -simplices into their -simplices
This appears spelled out for instance as (Goerss-Jardine 99, theorem 11.2).
In fact:
Proposition
is a cofibrantly generated model category with
Theorem
Let be the smallest class of morphisms in satisfying the following conditions:
- The class of monomorphisms that are in is closed under pushout, transfinite composition, and retracts.
- has the two-out-of-three property in and contains all the isomorphisms.
- For all natural numbers , the unique morphism is in .
Then is the class of weak homotopy equivalences.
Proof
- First, notice that the horn inclusions and are in .
- Suppose that the horn inclusion is in for all and all . Then for , the horn inclusion is also in .
- Quillen’s small object argument then implies all the trivial cofibrations are in .
- If is a trivial Kan fibration, then its right lifting property implies there is a morphism such that , and the two-out-of-three property implies is a trivial cofibration. Thus every trivial Kan fibration is also in .
- Every weak homotopy equivalence factors as where is a trivial Kan fibration and is a trivial cofibration, so every weak homotopy equivalence is indeed in .
- Finally, noting that the class of weak homotopy equivalences satisfies the conditions in the theorem, we deduce that it is the smallest such class.
As a corollary, we deduce that the classical model structure on is the smallest (in terms of weak equivalences) model structure for which the cofibrations are the monomorphisms and the weak equivalences include the (combinatorial) homotopy equivalences.
Proposition
Let be the connected components functor, i.e. the left adjoint of the constant functor . A morphism in is a weak homotopy equivalence if and only if the induced map
is a bijection for all Kan complexes .
Proof
One direction is easy: if is a Kan complex, then axiom SM7 for simplicial model categories implies the functor is a right Quillen functor, so Ken Brown’s lemma implies it preserves all weak homotopy equivalences; in particular, sends weak homotopy equivalences to bijections.
Conversely, when is a Kan complex, there is a natural bijection between and the hom-set , and thus by the Yoneda lemma, a morphism such that the induced morphism is a bijection for all Kan complexes is precisely a morphism that becomes an isomorphism in , i.e. a weak homotopy equivalence.
Properness
The Quillen model structure is both left and right proper. Left properness is automatic since all objects are cofibrant. Right properness follows from the following argument: it suffices to show that there is a functor which (1) preserves fibrations, (2) preserves pullbacks of fibrations, (3) preserves and reflects weak equivalences, and (4) lands in a category in which the pullback of a weak equivalence along a fibration is a weak equivalence. For if so, we can apply to the pullback of a fibration along a weak equivalence to get another such pullback in the codomain of , which is a weak equivalence, and hence the original pullback was also a weak equivalence. Two such functors are
- geometric realization , where denotes a sufficiently convenient category of topological spaces (e.g. the category of k-spaces suffices) and
- , where is the category of Kan complexes.
This may be found, for instance, in II.8.6–7 of Goerss-Jardine. Another proof may be found in Moss, and a different proof of properness may be found in Cisinski, Prop. 2.1.5.
Quillen equivalence with
Theorem
The singular simplicial complex/geometric realization-adjunction of example constitutes a Quillen equivalence of the classical model structure of def. with the classical model structure on topological spaces:
Proof
First of all, the adjunction is indeed a Quillen adjunction: prop. says in particular that takes Serre fibrations to Kan fibrations and prop. gives that sends monomorphisms of simplicial sets to relative cell complexes.
Now prop. says that the derived adjunction unit and counit are weak equivalences, and hence the Quillen adjunction is a Quillen equivalence.
Related concepts
References
Classical model structure on simplicial sets
On the classical model structure on simplicial sets:
The original proof is due to
- Daniel Quillen, Section II.3 of: Axiomatic homotopy theory in: Homotopical Algebra, Lecture Notes in Mathematics 43, Springer 1967(doi:10.1007/BFb0097438)
This proof is purely combinatorial (i.e. does not pass through geometric realization of simplicial sets as topological spaces): Quillen uses the theory of minimal Kan fibrations, the fact that the latter are fiber bundles, as well as the fact that the simplicial classifying space of a simplicial group is a Kan complex.
Other proofs are were given in:
-
Sergei Gelfand, Yuri Manin, Sections V.1-2 of: Methods of homological algebra, transl. from the 1988 Russian (Nauka Publ.) original, Springer 1996. xviii+372 pp. 2nd corrected ed. 2002 (doi:10.1007/978-3-662-12492-5)
-
Paul Goerss, J. F. Jardine, Section I.11 of: Simplicial homotopy theory, Progress in Mathematics, Birkhäuser (1999) Modern Birkhäuser Classics (2009) (doi:10.1007/978-3-0346-0189-4, webpage)
-
André Joyal, Myles Tierney, Notes on simplicial homotopy theory, Lecture at Advanced Course on Simplicial Methods in Higher Categories, CRM 2008 (pdf)
-
André Joyal, Myles Tierney An introduction to simplicial homotopy theory, 2005 (web, pdf)
A proof (in fact two variants of it) using the Kan fibrant replacement functor is given (in the context of_Cisinski model structure) in:
- Denis-Charles Cisinski, Section 2 of: Les préfaisceaux comme type d'homotopie, Astérisque, Volume 308, Soc. Math. France (2006), 392 pages (pdf)
The crucial step is the proof that the fibrations are precisely the Kan fibrations (and also to prove all the good properties of without using topological spaces); for two different proofs of this fact using , see Prop. 2.1.41 as well as Scholium 2.3.21 for an alternative). For the rest, everything was already in the book of Gabriel and Zisman, for instance.
Another approach using is:
- Sean Moss, Another approach to the Kan-Quillen model structure, Journal of Homotopy and Related Structures volume 15, pages 143–165 (2020) (arXiv:1506.04887, doi:10.1007/s40062-019-00247-y)
A proof of the model structure not relying on the classical model structure on topological spaces nor on explicit models for Kan fibrant replacement is in
- Christian Sattler, The Equivalence Extension Property and Model Structures (arXiv:1704.06911)
Proofs valid in constructive mathematics are given in:
-
Simon Henry, A constructive account of the Kan-Quillen model structure and of Kan’s Ex∞ functor, arXiv:1905.06160.
-
Nicola Gambino, Simon Henry, Christian Sattler, Karol Szumiło, The effective model structure and ∞-groupoid objects, arXiv:2102.06146.
As a categorical semantics for homotopy type theory, the model structure on simplicial sets is considered in
-
Chris Kapulkin, Peter LeFanu Lumsdaine, Vladimir Voevodsky, (arXiv:1203.2553)
-
Chris Kapulkin, Peter LeFanu Lumsdaine, The Simplicial Model of Univalent Foundations (after Voevodsky), Journal of the European Mathematical Society (arXiv:1211.2851,doi:10.4171/jems/1050)
Last revised on June 26, 2025 at 16:36:33. See the history of this page for a list of all contributions to it.