nLab metric Lie algebra

Defintion

A metric Lie algebra or quadratic Lie algebra over some ground field $\mathbb{F}$ is

1. Lie algebra $\mathfrak{g}$

2. a bilinear form $\mathfrak{g} \otimes \mathfrak{g} \overset{g}{\longrightarrow} \mathbb{F}$

such that $g$

1. is symmetric and invariant under the adjoint action, hence is an invariant polynomial on $\mathfrak{g}$;

2. is non-degenerate as a bilinear form, in that its tensor product-adjunct $\mathfrak{g} \to \mathfrak{g}^\ast$ is a linear isomorphism.

(But $g$ may be indefinite.)

The following table shows the data in a metric Lie representation equivalently

1. in category theory-notation;

2. in Penrose notation (string diagrams);

3. in index notation:

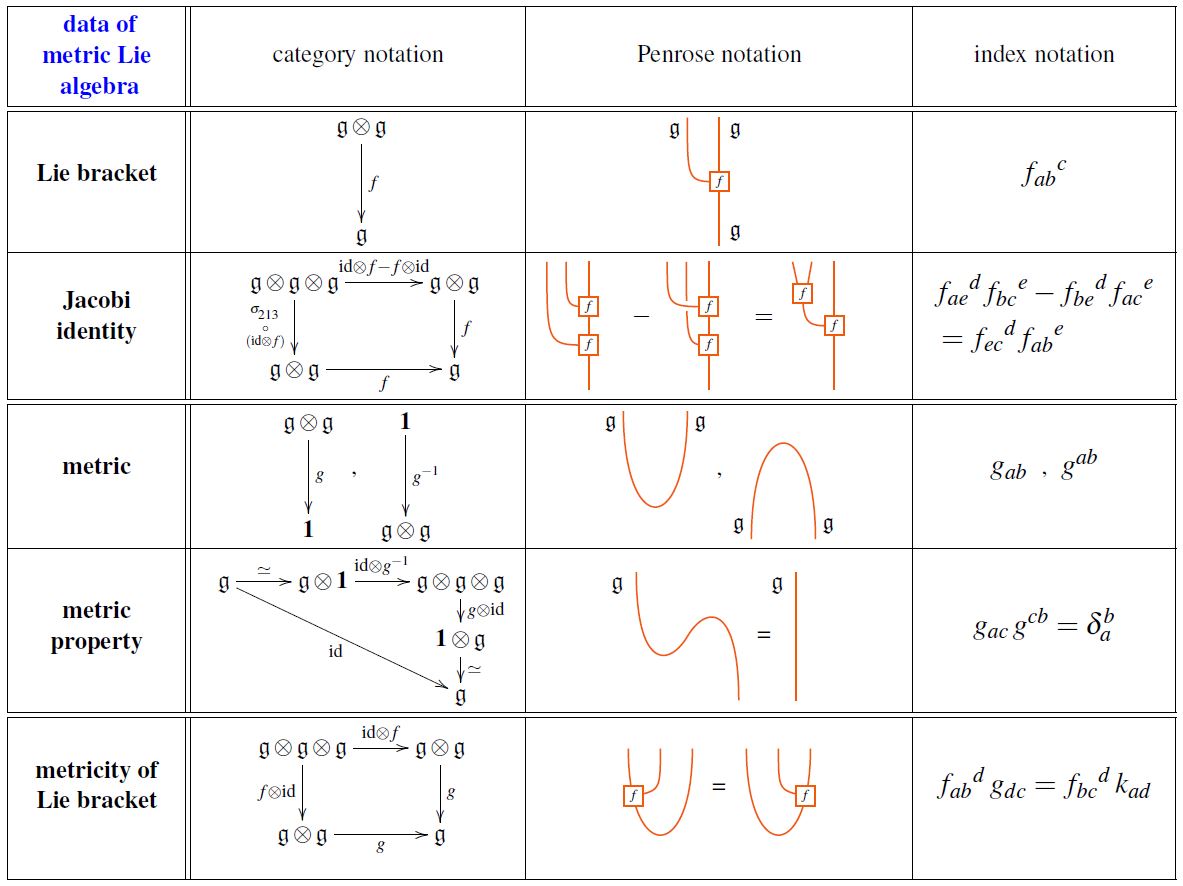
graphics from Sati-Schreiber 19c

Examples

• Every semisimple Lie algebra is a metric Lie algebra via its Killing form.

Applications

Lie algebra weight systems on chord diagrams

“Most” weight systems on chord diagrams come from metric Lie representations over metric Lie algebras: these are the Lie algebra weight systems.

Related concepts

• metric Lie representation

• Lie algebra weight system

• tensor network state

References

General

On the Faulkner construction:

• John Faulkner, On the geometry of inner ideals, Journal of Algebra, Volume 26, Issue 1, July 1973, Pages 1-9 (doi:10.1016/0021-8693(73)90032-X)

See also

• Wikipedia, Quadratic Lie algebra

Relation to M2-brane 3-Lie algebras

The full generalized axioms on the M2-brane 3-algebra and first insights into their relation to Lie algebra representations of metric Lie algebras is due to

• Sergey Cherkis, Christian Saemann, Multiple M2-branes and Generalized 3-Lie algebras, Phys. Rev. D78:066019, 2008 (arXiv:0807.0808)

The full identification of M2-brane 3-algebras with dualizable Lie algebra representations over metric Lie algebras is due to

• Paul de Medeiros, José Figueroa-O'Farrill, Elena Méndez-Escobar, Patricia Ritter, On the Lie-algebraic origin of metric 3-algebras, Commun. Math. Phys. 290:871-902, 2009 (arXiv:0809.1086)

reviewed in

• José Figueroa-O'Farrill, slide 145 onwards in: Triple systems and Lie superalgebras in M2-branes, ADE and Lie superalgebras, talk at IPMU 2009 (pdf, pdf)

further explored in

• José Figueroa-O'Farrill, Simplicity in the Faulkner construction, Journal of Physics A: Mathematical and Theoretical, Volume 42, Number 44 (arXiv:0905.4900)

and putting to use the Faulkner construction that was previously introduced in (Faulkner 73)

See also:

• Sam Palmer, Christian Saemann, section 2 of M-brane Models from Non-Abelian Gerbes, JHEP 1207:010, 2012 (arXiv:1203.5757)

• Patricia Ritter, Christian Saemann, section 2.5 of Lie 2-algebra models, JHEP 04 (2014) 066 (arXiv:1308.4892)

• Christian Saemann, appendix A of Lectures on Higher Structures in M-Theory (arXiv:1609.09815)