nLab mass term

Idea

In physics, a mass term is, quite generally, the summand in a Lagrangian density, Hamiltonian or equation of motion which expresses the mass of a given (quasi-)particle or field.

Often the terminology is used specifically for masses of spinors/Dirac fields, since here a mass term is subject to subtle constraints which may or may not exclude the mere existence of admissible mass terms.

Schematically, if a massless relativistic Dirac equation (here in Minkowski spacetime) is written in the form

$$\partial_0 \psi \;=\; k\!\!\!/ \cdot \psi \,,$$

where $k\!\!\!/$ are the Clifford momentum-operator, then for a mass term addition

$$\partial_0 \psi \;=\; k\!\!\!/ \cdot \psi \;+\; m \gamma_0 \,,$$

to lead to the required relativistic dispersion relation

$$E \,=\, \sqrt{k^2 + m^2}$$

one needs that the new Clifford-generator $\gamma_0$ exists as an operator on the given Hilbert space of spinor $\psi$ such that it skew-commutes with all the Clifford momenta

$$\gamma_0 \cdot k\!\!\!/ \;+\; k\!\!\!/\cdot \gamma_0 \;=\; 0 \,.$$

This is the kind of condition that also appears in Karoubi‘s formlation of topological K-theory-classes as equivalence classes of Clifford modules (see Freed & Hopkins 2021, Thm. 9.63).

In this guise, mass terms for electron-excitations in semi-metals play a role in the K-theory classification of topological phases of matter (see below).

Examples

In particle physics

In particle physics the (non-)existence of mass terms for fermionic fundamental particles goes along with their characterization as Dirac spinors, Weyl spinors and Majorana spinors.

This plays a central role notably in discussion of the (still hypothetical) detailed nature of neutrinos.

In topological phases of matter

In solid state physics of crystals, electrons are typically well-approximated by the non-relativistic Dirac equation, but around nodal points in the Brillouin torus, where electron bands cross, the effective dispersion relation is again of form of a relativistic Dirac- or Weyl-equation (whence one speaks of Dirac points or Weyl points).

(graphics from SS22)

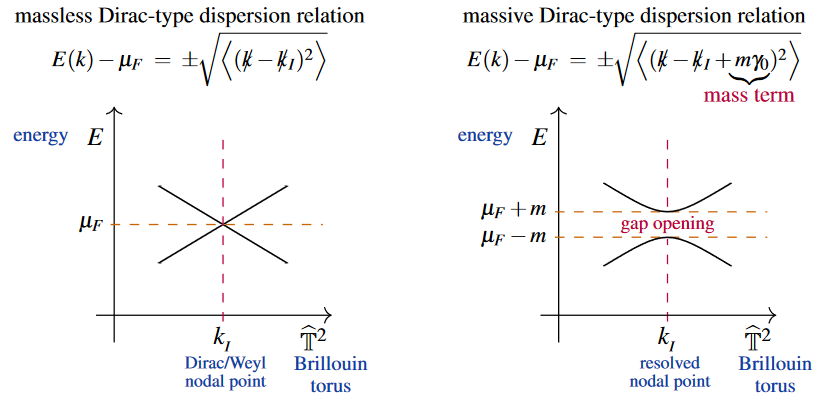
This phenomenon appears in particular in topological semi-metals, in which case the existence of a mass term, whose addition to the dispersion relation will remove the band crossing by “opening an energy gap”, is thought to signal the decay of the semi-metal-phase into a topological insulator-phase.

See for instance the example of the Haldane model.

Related concepts

• mass

• mass gap

• Karoubi K-theory

• K-theory classification of topological phases of matter

References

A careful discussion of relativistic mass terms is in:

• Daniel S. Freed, Michael J. Hopkins, Reflection positivity and invertible topological phases, Geom. Topol. 25 (2021) 1165-1330 $[$arXiv:1604.06527, doi:10.2140/gt.2021.25.1165$]$

Discussion aimed at the description of topological semi-metal-phases in solid state physics includes:

• Takahiro Morimoto and Akira Furusaki, Sec. V of: Topological classification with additional symmetries from Clifford algebras, Phys. Rev. B 88 (2013) 125129 (arXiv:1306.2505, doi:10.1103/PhysRevB.88.125129)

• Ching-Kai Chiu, Andreas P. Schnyder, Section A.2 of: Classification of reflection-symmetry-protected topological semimetals and nodal superconductors, Phys. Rev. B 90 205136 (2014) $[$doi:10.1103/PhysRevB.90.205136$]$

• Ching-Kai Chiu, Jeffrey C.Y. Teo, Andreas P. Schnyder, Shinsei Ryu, Section III.C of Classification of topological quantum matter with symmetries, Rev. Mod. Phys. 88 (2016) 035005 (arXiv:1505.03535, doi:10.1103/RevModPhys.88.035005)

See also discussion in the context of differential KO-theory:

• Kiyonori Gomi, Mayuko Yamashita, Differential KO-theory via gradations and mass terms [arXiv:2111.01377]

Some of the above material is taken from:

• Hisham Sati, Urs Schreiber: Topological Quantum Computation in TED-K