Schreiber Equivariant homotopy and super M-branes
An article that we have written:
-
John Huerta, Hisham Sati, Urs Schreiber,
Real ADE-equivariant (co)homotopy and Super M-branes
Communications in Mathematical Physics 371 (2019) 425
download:
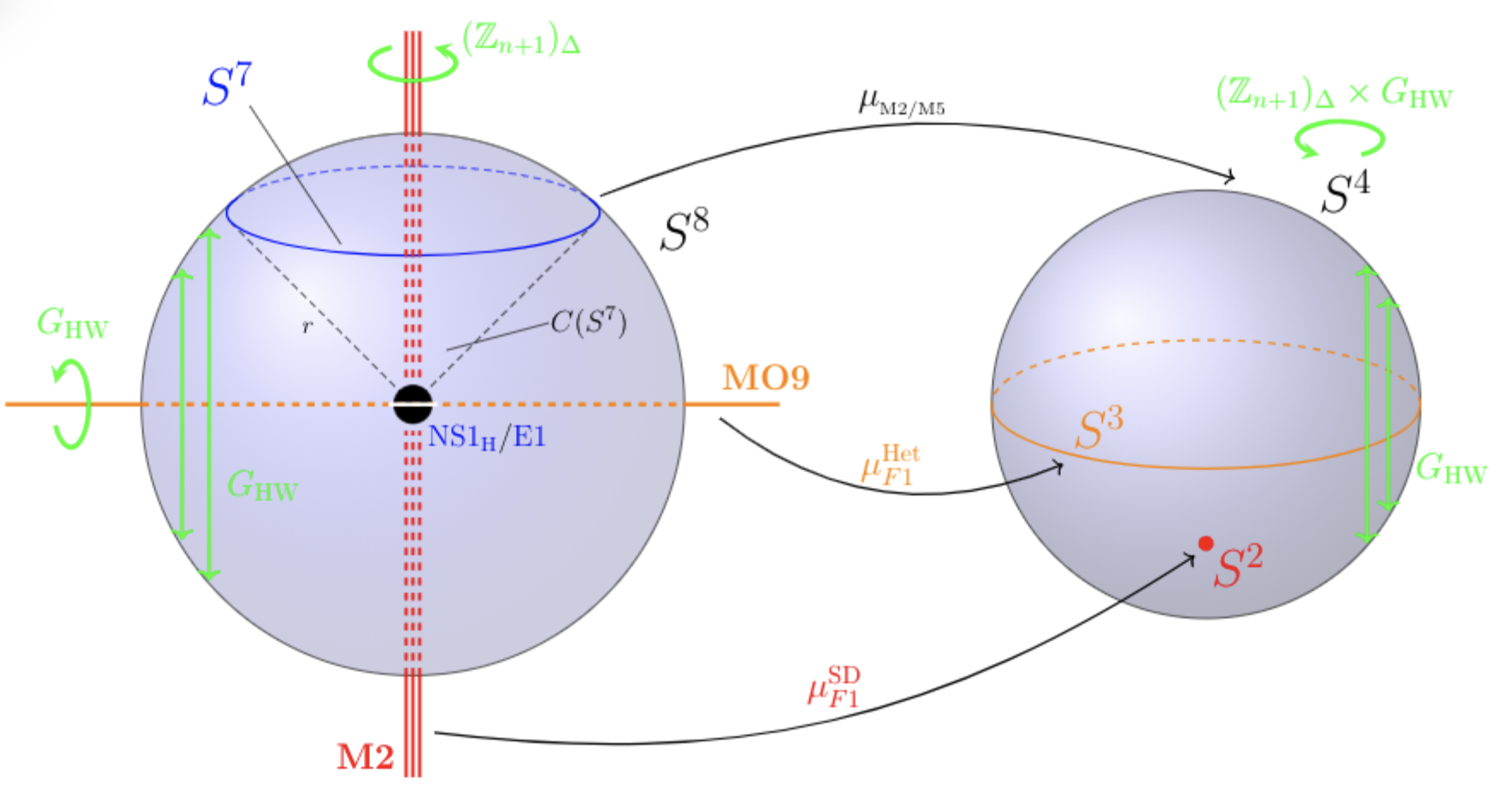
Abstract: A key open problem in M-theory is the identification of the degrees of freedom that are expected to be hidden at ADE-singularities in spacetime. Comparison with the classification of D-branes by K-theory suggests that the answer must come from the right choice of generalized cohomology theory for M-branes. Here we show that real equivariant cohomotopy on superspaces is a consistent such choice, at least rationally. After explaining this new approach, we demonstrate how to use Elmendorf's theorem in equivariant homotopy theory to reveal ADE-singularities as part of the data of equivariant 4-sphere-valued super-cocycles on 11d super-spacetime. We classify these super-cocycles and find a detailed black brane-scan that enhances the entries of the old brane scan to cascades of fundamental brane super-cocycles on strata of intersecting black M-brane species. At each stage the full Green-Schwarz action functional for the given fundamental brane species appears, as the datum associated to the morphisms in the orbit category.
Related Talk notes:
-
Structured Homotopy Theory from String Theory (pdf)
Related articles:
-
Super Lie n-algebra extensions, higher WZW models and super p-branes
-
T-Duality from super Lie n-algebra cocycles for super p-branes
all summed up in
and further developed in
See also
Last revised on June 13, 2023 at 16:54:38. See the history of this page for a list of all contributions to it.