nLab Green-Schwarz action functional
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Quantum field theory
Contents
- Idea
- Definition
- Properties
- Siegel- or -symmetry
- Dimensions – the brane scan
- The Brane molecule
- On curved spacetime and supergravity equations of motion
- Conserved currents
- As part of the AdS-CFT correspondence
- Quantization
- Related entries
- References
- Super-string as a GS-sigma model
- Super-membrane/M2-brane as a sigma model
- D-branes as GS-sigma models
- Dualities
- WZW terms, super Lie algebra cohomology and the brane scan
- Anti de Sitter backgrounds
- Self-dual strings in 6d
- General curved backgrounds and Supergravity background equations of motion
- Microscopic AdS/CFT via -brane sigma-models
- Conserved current algebra
- -Symmetry
- Open branes ending on other branes
Idea
Broad idea
The Green-Schwarz action functional is an action functional for a sigma-model that describes the propagation of a fundamental super -brane in a super spacetime supermanifold.
-
For this is the Green-Schwarz superparticle.
-
For this is the Green-Schwarz superstring (Green-Schwarz 84)
-
For this is the Green-Schwarz supermembrane (Bergshoeff-Sezgin-Townsend 87)
The Green-Schwarz model of the superstring is in contrast to the NSR-string model (the original spinning string), which has manifest worldsheet supersymmetry but no manifest spacetime supersymmetry. It is a non-trivial theorem that the spectrum of the NSR-string enjoys spacetime supersymmetry (after GSO projection) and may hence be identified with perturbative excitations of a supergravity background. The construction of the Green-Schwarz functional was motivated by the desire to find an equivalent alternative formulation in which spacetime supersymmetry is manifest (see e.g. Schwarz 16, slides 24-25).
manifest supersymmetry for brane sigma-models:
| manifest worldvolume supersymmetry | manifest target+worldvolume supersymmetry | manifest target space supersymmetry |
|---|---|---|
| NSR action functional | superembedding approach | Green-Schwarz action functional |
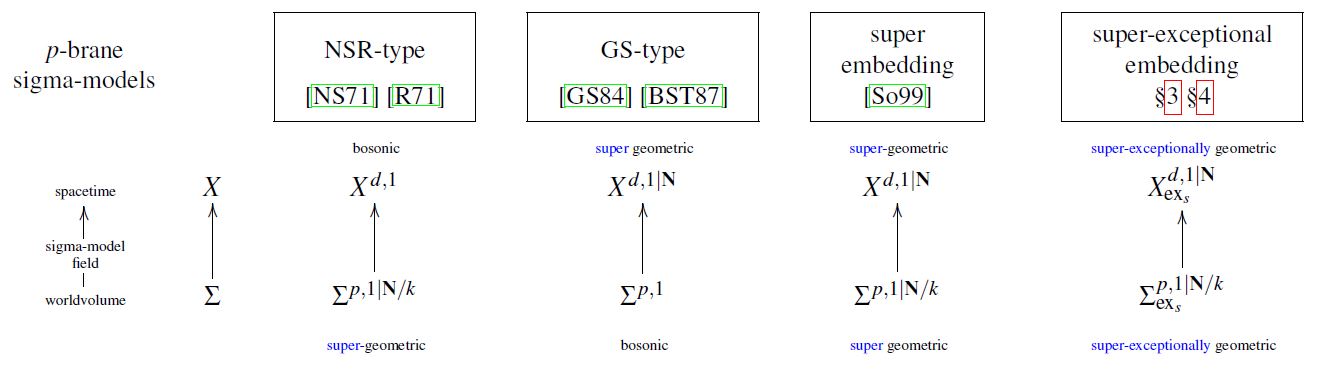
graphics grabbed from FSS19c
For more discussion see also at geometry of physics – fundamental super p-branes.
More details
Perturbativestring theory on geometric backgrounds is defined by the Neveu-Schwarz-Ramond model, namely by sigma-model 2d super conformal field theories (of central charge 15) on worldsheets that are super Riemann surfaces, with target spaces that are ordinary (i.e. “bosonic”) spacetime manifolds.
These worldsheet field theories are induced from action functionals, namely from variants of the standard energy functional (Polyakov action) on the mapping space of smooth functions
from the worldsheet to target spacetime .
The central theorem of perturbative superstring theory (the no ghost theorem with GSO projection) says that the excitation spectrum of such a 2d SCFT are the quanta of the perturbations of a higher dimensional effective supergravity field theory on target spacetime, hence transforms under supersymmetry on target spacetime.
This is the fundamental prediction of the assumption of fundamental strings:
-
assuming that the fundamental particles that run in Feynman diagrams are fundamentally (at high energy) the ground state modes of a fundamental string,
-
demanding that there are fermionic particles among these,
implies
-
that the string must be the spinning string (have fermions in its worldsheet theory), which in turn implies…
-
that it is the superstring (worldsheet supersymmetry mixes the worldsheet bosons and fermions), precisely: the Neveu-Schwarz-Ramond superstring, which then in addition implies…
-
that its target space effective field theory is a supergravity theory, hence that also the effective target space fields exhibit local supersymmetry (i.e. “high energy supersymmetry”, different from “low energy supersymmetry” that the LHC was looking for).
| main theorem of perturbative super-string theory |
|---|
The first step in this implication (identifying the spinning string as the superstring) is fairly straightforward (in fact this is how the concept of supersymmetry was discovered in “the west”, in the first place), but the second step (that the superstring excitations necessarily are quanta of a spacetime supergravity theory) appears as a miracle from the point of view of the Neveu-Schwarz-Ramond superstring. It comes out this way by non-trivial computation, but is not manifest in the theory.
In order to improve on this situation, Michael Green and John Schwarz searched for and found (Green-Schwarz 81, Green-Schwarz 82 Green-Schwarz 84, for the history see Schwarz 16, slides 24-25) a suitably equivalent string action functional that would manifestly exhibit spacetime supersymmetry. Acordingly, this is now called the Green-Schwarz action functional.
| action functional for superstring | manifest supersymmetry |
|---|---|
| Neveu-Ramond-Schwarz super-string | on worldsheet |
| Green-Schwarz super-string | on target spacetime |
The basic idea is to pass to the evident supergeometric analogue of the bosonic string action:
Let be a closed manifold of dimension 2 – representing the abstract worldsheet of a string. Let be a pseudo-Riemannian manifold – representing a purely gravitational spacetime background. Then the action functional governing the bosonic string propagating in this spacetime is the functional
on the smooth mapping space (of smooth functions ), that simply assigns the proper relativistic volume of the image of the worldsheet in spacetime:
(This is the Nambu-Goto action. It is classically equivalent to the Polyakov action which is the genuine starting point for the quantum Neveu-Ramond-Schwarz super-string. However, since, as we discuss below, the Green-Schwarz action naturally generalizes to that of other p-branes it is more natural to consider the Nambu-Goto form of the action here.)
When here is generalized to a superspacetime supermanifold with orthogonal structure encoded by a super-vielbein , then the same form of the action functional still makes sense and produces a functional on the supergeometric mapping space . Moreover, by construction this action functional now is invariant under the superisometry group of , hence under global spacetime supersymmetry.
However, Green and Schwarz noticed that this kinetic action functional does not quite yield dynamics that is equivalent to that of the Neveu-Schwarz-Ramond super-string: when the equations of motion hold (“on shell”) it has more fermionic degrees of freedom than present in the Neveu-Ramond-Schwarz super-string. The key insight of Green and Schwarz was that one may add an extra summand (whose notation we explain in a moment) to the plain super-Nambu-Goto action , such that the resulting action functional enjoys a further 1-parameter symmetry, called kappa-symmetry. This is the Green-Schwarz action functional:
Moreover, they showed that restricting the dynamics of the Green-Schwarz superstring to the -symmetric states, then it does become equivalent, classically to that of the Neveu-Ramond-Schwarz super-string.
Finally they showed that when gauge fixing the Green-Schwarz action functional to light-cone gauge (which is possible whenever target spacetime admits two lightlike Killing vector) then the Green-Schwarz string may be quantized by a standard procedure and the resulting quantum dynamics is equivalent to that of the Neveu-Schwarz-Ramond super-string. This provides the desired conceptual proof for the observed local target spacetime supersymmetry of super-string effective field theory, at least for backgrounds that admit two lightlike Killing vectors. (The quantization of the Green-Schwarz superstring away from light cone gauge remains an open problem.)
While Green-Schwarz’s extra kappa-symmetry term this serves a clear purpose as a means to an end, originally its geometric meaning was mysterious. However, in (Henneaux-Mezincescu 85) it was observed (expanded on in (Rabin 87, Azcarraga-Townsend 89, Azcarraga-Izquierdo 95,chapter 8)), that the Green-Schwarz action functional describing the super-string in -dimensions does have a neat geometrical interpretation: it is simply the (parameterized) Wess-Zumino-Witten model for
-
target space being locally super Minkowski spacetime regarded as the coset supergroup
for a real spin representation (the “number of supersymmetries”), the corresponding super Poincaré group and its Lorentz-signature Spin subgroup;
-
WZW-term being a local potential for the unique (up to rescaling, if it exists) -invariant super Lie algebra 3-cocycle on the super Poincaré Lie algebra , with components locally given by the Gamma-matrices of the given Clifford algebra representation; in terms of the super vielbein :
and so in components the bi-fermionic component of is
and all other components vanish.
More in detail, just as ordinary Minkowski spacetime may be identified with the translation group along itself, with canonical linear basis of left invariant 1-forms given by the canonical vielbein field
where are the canonical coordinates on , so super Minkowski spacetime for some real spin representation is characterized as the supergroup whose left invariant 1-forms constitute the -bigraded differential with generators the super-vielbein
where are the canonical coordinates on , with the odd-graded elements spanning the given real Spin(d-1,1)-representation with Clifford algebra generators .
Now while ordinary Minkowski spacetime is an abelian group, reflected by the fact that its left-invariant 1-forms are all closed
the key phenomenon of supersymmetry (that two fermions pair to a bosons) means that is slightly non-abelian, reflected by the fact that the super-vielbein is not closed
This elementary effect is the source of all the rich structure seen in the Green-Schwarz super-string and generally in all super p-brane theory. (The above differential is equivalently that in the Chevalley-Eilenberg algebra of super Minkowski spacetime, hence its cohomology is the super-Lie algebra cohomology of super Minkowski spacetime. In parts of the physics literature this is referred to a “tau cohomology”.)
In particular, for special combinations of spacetime dimension and number of supersymmetries (i.e. real spin representation ) then the 3-form
is a non-trivial super Lie algebra cocycle on , in that and so that there is no left invariant differential form with (beware here the left-invariance condition: there are of course non-left-invariant potentials for , and in fact these are exactly the possible Lagrangian densities for the WZW action functional ).
This happens notably for
-
and (heterotic string)
-
and (type IIB superstring)
-
and (type IIA superstring).
(It also happens in some lower dimensions, where however the corresponding Neveu-Schwarz-Ramond string develops a conformal anomaly after quantization (a “non-critical string”). This classification of cocycles is part of what has come to be known as the brane scan in superstring theory, see below.)
In this equivalent formulation, the Green-Schwarz action functional for the superstring has the following simple form:
Let be a superspacetime, hence a supermanifold equipped with a super-vielbein (super-orthogonal structure) which is locally modeled on (technically: a torsion-free super-Cartan geometry modeled on ). Write for the super differential form on which is the induced definite globalization of the cocycle over . For any contractible subspace, then the restriction of of to is exact, and hence admits a potential , i.e. such that .
Then for a 2-dimensional closed manifold, the Green-Schwarz action functional
is the function on the super-smooth mapping space of morphisms of supermanifolds which factor through , given by
In order to get rid of the restriction to some chart one needs to add global data. The need for this is at least mentioned briefly in (Witten 86, p. 261 (17 of 20)), but seems to have otherwise been ignored in the physics literature. The general solution is to promote the local potentials to the connection on a super gerbe (FSS 13). This is a choice of higher prequantization
Writing for the volume holonomy of a circle 2-bundle with connection , then the globally defined Green-Schwarz sigma model
is given by
This form of the Green-Schwarz action functional for the string has evident generalization to other p-branes. Whenever there is a Spin(d-1,1)-invariant -cocycle on , then one may ask for a higher gerbe (higher prequantum line bundle) with curvature and consider the analogous functional.
The triples (spacetime dimension, number of supersymmetries, dimension of brane) such that
is a nontrivial cocycle, hence for which there is such a Green-Schwarz action functional for -branes on may be classified and form what is called the brane scan (Achúcarro, Evans, Townsend & Wiltshire 87, Brandt 12-13):
The graphics on the left is from (Duff 87). The diagonal lines indicate double dimensional reduction, taking a -brane in dimensions to a -brane in -dimensions.
For instance for one finds a cocycle, and the corresponding GS-action functional is that of the fundamental M2-brane.
This was a striking confluence of brane physics and classification of super Lie algebra cohomology. But just as striking as the matching, was what it lacked to match: the D-branes and the M5-brane (, ) are lacking from the old brane scan. Incidentally, these lacking branes are precisely those branes on which the branes that do appear on the brane scan may end, equivalently those branes that have higher gauge fields on their worldvolume (tensor multiplets).
An action functional for the M5-brane analogous to a Green-Schwarz action functional was found in (BLNPST 97, APPS 97). It is again the sum of a kinetic term and a WZW-like term, but the WZW-like term does not come from a cocycle on a (super-)group.
In order to deal with this, it was suggested in (CAIB 99, Sakaguchi 00, Azcarraga-Izquierdo 01) that there is an algebraic structure called “extended super-Minkowski spacetimes” that generalizes super Minkowski spacetime and serves to unify the Green-Schwarz-like models for the D-branes and the M5-brane with the original Green-Schwarz models for the string and the M2-brane.
These extended super-Minkowski spacetimes carry algebraic analogs of super Lie algebra cocycles, such that the relevant terms for the D-branes and the M5-brane do appear after all, hence such that all the branes in string theory/M-theory are unified. In fact these “extended super-Minkowski spacetimes” are precisely the “FDA”s that have been introduced before in the D'Auria-Fré formulation of supergravity and what became identified as the 7-cocycle for the M5-brane this way had earlier been recognized algebraically as an stepping stone for an elegant re-derivation of 11-dimensional supergravity (D’Auria-Fré 82).
The (higher) geometric meaning of these constructions was found in (Fiorenza-Sati-Schreiber 13): these algebraic structures of “extended super-Minkowski spacetimes”/FDAs are precisely the Chevalley-Eilenberg algebras of super Lie n-algebra-extensions of super-Minkowski spacetime which are classified by the cocycles that serve as the GS-WZW terms of the -branes that may end on those -branes whose cocycles are carried by the extended super-Minkowski spacetime.
Hence the missing -branes in the old brane scan (classifying just cocycles on super Lie algebras) do appear as one generalizes (super) Lie algebras to (super) strong homotopy Lie algebras = L-infinity algebras. Moreover, each brane intersection law (one brane species may end on another) is now matched to a super -algebra extension and so the old brane scan is generalized to a tree of branes The brane bouquet:
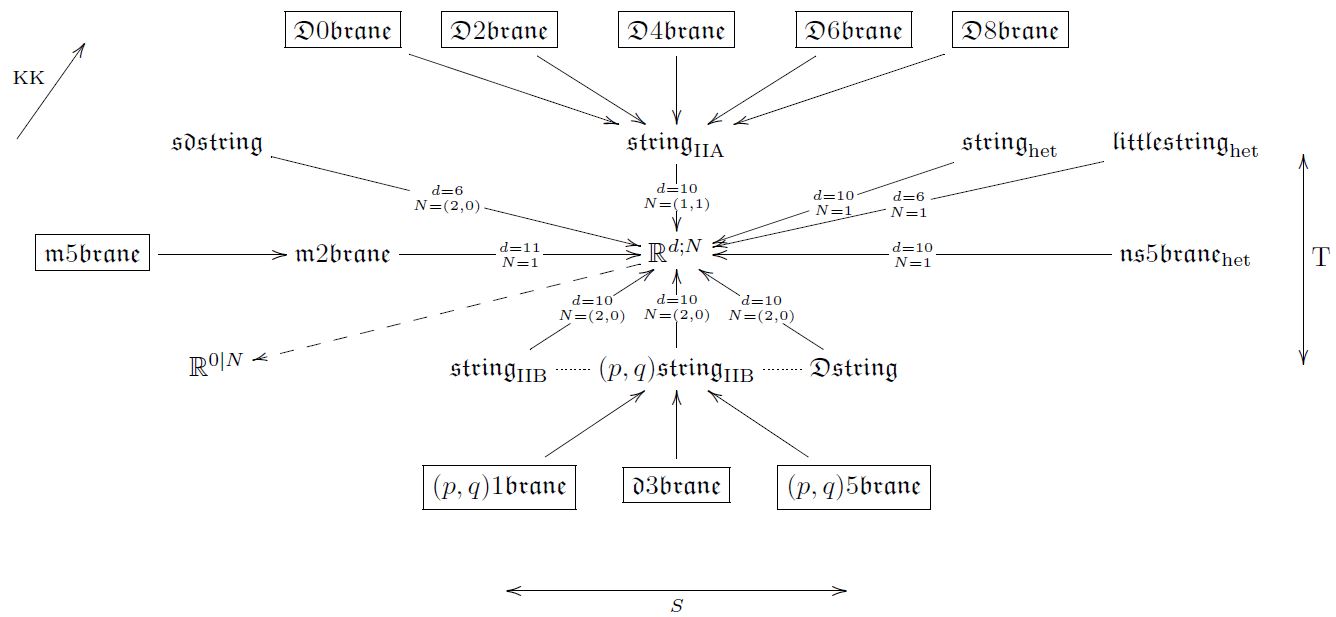
Each item in this bouquet denotes a super L-infinity algebra and each arrow denotes an L-infinity extension classified by a cocycle which encodes the GS-WZW term of the brane named by the domain of the arrow. Moreover, arrows pass exactly from one brane species to the brane species that may end on the former.
In (Fiorenza-Sati-Schreiber 13) it is shown that all these super L-infinity algebras Lie integrate to smooth super-n-groups, and all the cocycles Lie integrate to super-gerbes on these, such that the induced volume holonomy is the relevant generalized GS-WZW term. For detailed exposition see at Structure Theory for Higher WZW Terms.
With this generalized perspective, now the Green-Schwarz-type action functionals describe all the p-branes in string theory/M-theory.
Again, in order to make this generally true one needs to apply a higher prequantization – a choice of line (p+1)-bundle with connection – in order to globalize the WZW-terms (Fiorenza-Sati-Schreiber 13)
Hence is the actual background field that the -brane couples to. There is considerably more information in than in its curvature . For instance for the M2-brane one may find the local super moduli space for local choices of for the given on KK-compactifications to . It turns out that the bosonic body of this moduli space is the exceptional tangent bundle on which the U-duality group E7 has a canonical action (see at From higher to exceptional geometry).
This highlights that Green-Schwarz functionals capture fundamental (“microscopic”) aspects of -branes. In contrast, often -branes are discussed in their solitonic incarnation as black branes. These solitonic branes sit at asymptotic boundaries of anti-de Sitter spacetime and carry conformal field theories, related to the ambient supergravity by AdS-CFT duality.
This phenomenon is indeed a consequence of the fundamental Green-Schwarz branes:
Consider a 1/2-BPS state solution of type II supergravity or 11-dimensional supergravity, respectively. These solutions locally happen to have the same classification as the Green-Schwarz branes. Hence we may consider a configuration of the corresponding fundamental -brane which embeds into the asymptotic AdS boundary of the given 1/2 BPS spacetime . Then it turns out that restricting the Green-Schwarz action functional to small fluctuations around this configuration, and applying a diffeomorphism gauge fixing, then the resulting action functional is that of a supersymmetric conformal field theory on as in the AdS-CFT dictionary:
| fundamental -brane | -fluctuations about asymptotic AdS configuration | solitonic -brane |
|---|---|---|
| Green-Schwarz action functional | super-conformal field theory |
(Claus-Kallosh-Proeyen 97, Claus-Kallosh-Kumar-Townsend 98, AFFFTT 98 Pasti-Sorokin-Tonin 99)
In fact the BPS-state condition itself is neatly encoded in the Green-Schwarz action functionals: by construction they are invariant under the spacetime superisometry group. Hence the Noether theorem implies that there are corresponding conserved currents, whose Dickey bracket forms a super-Lie algebra extension of the Lie algebra of supersymmetries.
Here the “” filling the triangles is the non-trivial gauge transformation by which the WZW term (as any WZW term) is preserved under the symmetries (instead of being fixed identically). It is the information in this transformations which makes the currents form an extension of the symmetries.
Here this yields the famous brane charge extensions of the super-isometry super Lie algebra of the schematic form
(for a Killing spinor and its corresponding Killing vector) known as the type II supersymmetry algebra and the M-theory supersymmetry algebra, respectively (Azcárraga-Gauntlett-Izquierdo-Townsend 89). In fact it yields super-Lie n-algebra extensions of which the familiar super Lie algebra extensions are the 0-truncation (Sati-Schreiber 15, Khavkine-Schreiber 16).
In summary, the nature and classification of Green-Schwarz action functionals captures in a mathematically precise way a good deal of the core structure of string/M-theory.
In fact, the super Lie-n algebraic perspective on the Green-Schwarz functionals via the brane bouquet also solves the following open problem on M-branes:
it is famously known from Freed-Witten anomaly-cancellation that the D-brane charges are not in fact just in de Rham cohomology in every second degree, but are in twisted K-theory, hence rationally in twisted de Rham cohomology, with the twist being the F1-brane charge (from the fundamental). It is an open problem to determine what becomes of these twisted K-theory charge groups as one lifts F1/D-branes in string theory to M2/M5-branes in M-theory.
| intersecting branes | charges in generalized cohomology theory | |
|---|---|---|
| string theory | F1/Dp-branes | twisted K-theory |
| M-theory | M2/M5-branes | ??? |
Notice that there are “microscopic degrees of freedom” of the theory encoded by the choice of generalized cohomology theory here, generalizing the extra degrees of freedom in the choice of a WZW-term already mentioned above. In general for a cohomology theory and its Chern character map (for instance from topological K-theory to ordinary cohomology in every second degree), then a choice of genuine charges is the extra information encoded in a lift
But rationally The brane bouquet allows to derive this from first principles:
Above we saw that the naive cocycles of the D-branes and of the M5-brane are not defined on the actual spacetime, but on some “extended” spacetime, which is really a smooth super infinity-groupoid extension of spacetime. Hence we should ask if these cocycles descend to the actual super-spacetime while picking up some twists.
One may prove that:
-
the F1/D-brane GS-WZW cocycles descend to 10d type II superspacetime to form a single cocycle in rational twisted K-theory, just as the traditional lore reqires (Fiorenza-Sati-Schreiber 16);
-
the M2/M5 GS-WZW cocycles descent to 11d superspacetime to form a single cocycle with values in the rational 4-sphere (Fiorenza-Sati-Schreiber 16).
This has implications on some open conjectures regarding M-theory, for more on this see Equivariant cohomology of M2/M5-branes.
Definition
The Green-Schwarz action functionals are of the standard sigma-model form for target spaces that are super-homogeneous spaces for a Lie supergroup and a sub-super-group, and for background gauge fields that are super-WZW-circle n-bundles with connection/bundle gerbes on .
- for branes on super Minkowski spacetime: is the super Poincaré Lie algebra and the Lorentz Lie algebra;
These action functionals were first considered in (Green-Schwarz 84) for superstrings in various dimensions. The full interpretation of the action functional as an higher Wess-Zumino-Witten theory-type action controled by the Lie algebra cohomology of the super Poincaré Lie algebra (or rather of the super translation Lie algebra inside it) is due to (Azcárraga-Townsend89).
- for branes on super anti de Sitter spacetime, is a superconformal group (e.g. Metsaev-Tseytlin 98, section 3)
Supercoordinates
We briefly review some basics of the canonical coordinates and the super Lie algebra cohomology of the super Poincaré Lie algebra and super Minkowski space, which are referred to below (see for instance Azcárraga-Townsend 89, and see at super Cartesian space and at signs in supergeometry.).
By the general discussion at Chevalley-Eilenberg algebra, we may characterize the super Poincaré Lie algebra by its CE-algebra “of left-invariant 1-forms” on its group manifold.
Definition
The Chevalley-Eilenberg algebra is generated on
-
elements and of degree
-
and elements of degree
with the differential defined by
Removing the terms involving here this is the super translation algebra.
In this way the super-Poincaré Lie algebra and its extensions is usefully discussed for instance in (D’Auria-Fré 82) and in (Azcárraga-Townsend 89, CAIB 99). In much of the literature instead the following equivalent notation is popular, which more explicitly involves the coordinates on super Minkowski space.
Remark
The abstract generators in def. are identified with left invariant 1-forms on the super-translation group (= super Minkowski space) as follows.
Let be the canonical coordinates on the supermanifold underlying the super translation group. Then the identification is
-
.
-
.
Notice that this then gives the above formula for the differential of the super-vielbein in def. as
Remark
The term is sometimes called the supertorsion of the super-vielbein , because the defining equation
may be read as saying that is torsion-free except for that term. Notice that this term is the only one that appears when the differential is applied to “Lorentz scalars”, hence to object in which have “all indices contracted”. (See also at torsion constraints in supergravity.)
Notably we have
This remaining operation “” of the differential acting on Loretz scalars is sometimes denoted “”, e.g. in (Bossard-Howe-Stelle 09, equation (8)).
This relation is what govers all of the exceptional super Lie algebra cocycles that appear as WZW terms for the Green-Schwarz action below: for some combinations of a Fierz identity implies that the term
vanishes identically, and hence in these dimensions the term
is a cocycle. See also the brane scan table below.
Kinetic term
(…)
(…)
WZW term
Let be the standard generators of the Chevalley-Eilenberg algebra of the super Poincaré Lie algebra, as discussed there.
The part of the Lie algebra cohomology of the super translation Lie algebra that is invariant under the Lorentz transformations is spanned by closed elements of the form
These exist (are closed) only for certain combinations of and . The possible values are listed below.
For a bosonic WZW model the background gauge field induced by such a cocycle would be the corresponding Lie integration to a circle n-bundle with connection. Here, since the super translation group is contractible, a Poincaré lemma applies and these circle -connections are simply given by globally defined connection form satisfying
The WZW part of the GS action is then
(…)
Properties
Siegel- or -symmetry
The Green-Schwarz action has an extra fermionic symmetry, on top of the genuine supersymmetry, first observed in (Siegel 83) for the superparticle and in (Siegel 84) for the super 1-brane in 3d, and finally in (GreenSchwarz 84) for the critical superstring in 10-dimensions. This is also called kappa-symmetry. It has a natural interpretation in terms of the super-Cartan geometry of target space (McArthur, GKW). Discussion from the point of view of the D'Auria-Fré formulation of supergravity is in (AFFFTT 98, section 3, Fré-Grassi 07, section 2.2).
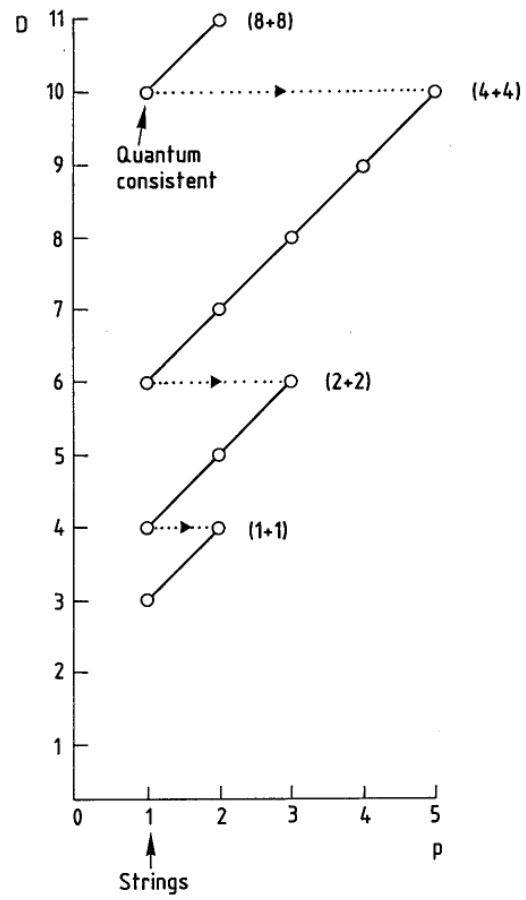
Dimensions – the brane scan
The Green-Schwarz action functional of a -brane propagating on an -dimensional target spacetimes makes sense only for special combinations of , for which there are suitanble super Lie algebra cocycles on the super translation Lie algebra (see above).
The corresponding table has been called the brane scan in the literature, now often called the “old brane scan”, since it has meanwhile been further completed (see below). In (Duff 87) the “old brane scan” is displayed as follows.

In the -row we see the critical superstring of string theory and its magnetic dual, the NS5-brane. The top row shows the M2-brane in 11-dimensional supergravity.
Moving down and left the diagonals corresponds to double dimensional reduction.
Remark
The first non-empty column of the table is a reflection of the exceptional isomorphisms of the spin group in low dimensions and the normed division algebras:
exceptional spinors and real normed division algebras
Remark
What is missing in the “old brane scan” are the D-branes in and the M5-brane in (See also BPST). The reason is that the M5 corresponds to a 7-cocycle not on the ordinary super Poincaré Lie algebra, but on its L-infinity algebra extension, the supergravity Lie 3-algebra. The completion in super L-infinity algebra theory is discussed in (FSS 13), as The brane bouquet.
So (with notation as above) we have the following.
The brane scan.
The Green-Schwarz type super -brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | M2 | M5 | ||||||||
| 10 | D0 | F1, D1 | D2 | D3 | D4 | NS5, D5 | D6 | D7 | D8 | D9 |
| 9 | * | |||||||||
| 8 | * | |||||||||
| 7 | M2 | |||||||||
| 6 | F1, S1 | S3 | ||||||||
| 5 | * | |||||||||
| 4 | * | * | ||||||||
| 3 | * |
(The first columns follow the exceptional spinors table.)
The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | on sIso(10,1) | on m2brane | ||||||||
| 10 | on sIso(9,1) | on StringIIA | on StringIIB | on StringIIA | on sIso(9,1) | on StringIIA | on StringIIB | in StringIIA | on StringIIB | |
| 9 | on sIso(8,1) | |||||||||
| 8 | on sIso(7,1) | |||||||||
| 7 | on sIso(6,1) | |||||||||
| 6 | on sIso(5,1) | on sIso(5,1) | ||||||||
| 5 | on sIso(4,1) | |||||||||
| 4 | on sIso(3,1) | on sIso(3,1) | ||||||||
| 3 | on sIso(2,1) |
The Brane molecule
Furthermore, there exists a more general classification of possible supermembranes in spacetime with spatial dimensions and time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.
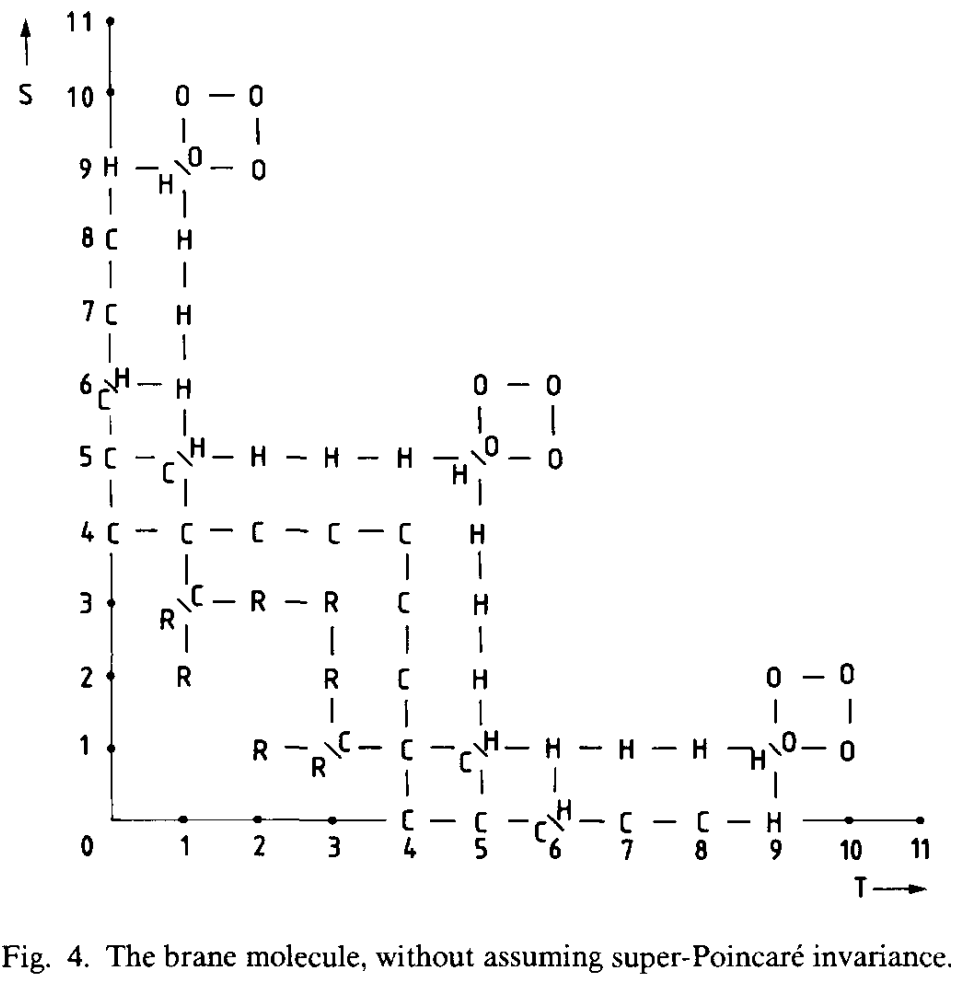
Compare:
-
Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)
On curved spacetime and supergravity equations of motion
In the first order formulation of gravity a field configuration on a spacetime manifold is a Cartan connection
hence a principal connection for the super Poincaré group such such that at each point it identifies the tangent space with
Hence given a Lie algebra cocycle
as for the Green-Schwarz superstring we can pull it back along this Cartan connection to a differential 3-form on spacetime.
In general this 3-form is no longer closed. If it is closed, then the Green-Schwarz superstring is again well defined on as a WZW model.
The claim now is that requiring this 3-form still to be closed is, as a condition on the field of gravity , precisely the equations of motion of supergravity (the super-Einstein equations).
This is due to (Nilsson 81, Bergshoeff-Sezgin-Townsend 86) and others, see the references below.
Membrane in 11d SuGra background
For the membrane(M2-brane) in a background of 11-dimensional supergravity (Bergshoeff-Sezgin-Townsend 87) find that consistency requires that (in a given coordinate chart with super-vielbein field ) the 4-form flux is of the form
where the first summand is the super-Lie algebra cocycle that classifies the supergravity Lie 3-algebra and the second is the field strength of the supergravity C-field proper (hence a purely bosonic differential form). In the second line we have rewritten this more manifestly in terms of the super-vielbein , this way the expression is directly analogous to that of definite 3-forms in the theory of G₂-manifolds (see this example for details).
Moreover the torsion tensor is to have its -component equal to , see at torsion constraints in supergravity.
In addition the Bianchi identities have to hold:
All this is implied by the equations of motion of 11-dimensional supergravity.
Notice that in view of the above analogy to G₂-structure, the covariant constancy condition is precisely the analog of G₂-manifold structure.
Discussion of this in the somewhat more streamlined D'Auria-Fré formulation of supergravity is in (AFFFTT 98, section 3.1).
Heterotic string
Discussion that for the GS-version of the heterotic string consistency of the background is equivalent to the equations of motion of heterotic supergravity is in (Shapiro-Taylor 87).
Discussion with the hetetoric gauge field included is in (Atick-Dhar-Ratra 86).
Type II string
Discussion for the GS-version of the type II superstring in type II supergravity-backgrounds is in (GHMNT 85), and for the D-branes in type II in (CGNSW 97).
Conserved currents
The super-WZW term of the GS action functionals is invariant under supersymmetry only up to a divergence. Hence the Noether theorem in its generality for “weak” symmetries applies and gives that the conserved currents receive an extra contribution from this divergence term. The resulting algebra is a central extension of the given super translation Lie algebra, extending to the famous polyvector extensions “by brane charges” of the super Poincaré Lie algebra (AGIT 89).
As part of the AdS-CFT correspondence
By the above discussion, Green-Schwarz super -branes are consistent on superspacetimes that satisfy the respective higher supergravity equations of motion. These turn out to have solutions which exhibit black branes in essentially just the combinations of dimensions and supersymmetries that the original Green-Schwarz sigma-models exist in, hence they look precisely like the non-perturbative avatars of whatever these sigma models give the perturbation theory of by second quantization. (See at black holes in string theory for more on this correspondence between branes in string perturbation theory and black branes in supergravity.)
Moreover, the near-horizon geometries of these black branes are always anti de Sitter spacetime times orthogonal directions.
Therefore it is natural to consider the perturbation of the Green-Schwarz sigma-models around their asymptotic embeddings into AdS spaces, hence effectively the perturbation theory of the degrees of freedom at those naked singularity at which the corresponding black brane sits.
After diffeomorphism gauge fixing one finds that the resulting field theories now on the -brane worldvolumes are precisely the superconformal field theories for all the allowed superconformal supersymmetries (see also at singleton representation):
| superconformal super Lie algebra | R-symmetry | brane worldvolume theory | ||
|---|---|---|---|---|
| 3 | osp | |||
| 3 | osp | M2-brane | ||
| 4 | D3-brane | |||
| 5 | 1 | |||
| 6 | osp | M5-brane |
This is effectively the AdS-CFT correspondence.
Detailed discussion of the above steps is in (AFFFTT 98, Pasti-Sorokin-Tonin 99). The resulting “super-conformal brane scan” is discussed in Blencowe & Duff 1988 with further developments in Duff 2009, Duff 2021.
Quantization
The quantization of the Green-Schwarz super -brane sigma models is discussed in the literature in terms of light-cone gauge quantization.
This is actually how the Green-Schwarz superstring was first introduced in (Green-Schwarz 81, Green-Schwarz 82) before its generally covariant formulation was found in (Green-Schwarz 84). A textbook account of this is in (Green-Schwarz-Witten, section 5).
While, by the brane scan discussed above, the action functional for the Green-Schwarz superstring exists for target super Minkowski spacetimes of dimension , 4, 6, and 10, its light-cone gauge quantization produces a quantum anomaly for the spacetime Lorentz group symmetry in dimension and . For the anomaly disappears and the thus quantized Green-Schwarz string becomes equivalent to the quantum NSR string, hence to “the” critical string (of heterotic string theory, type II string theory).
Curiously, the light-cone gauge quantization of the GS-string also does wor however for , see at super 1-brane in 3d for more on this.
(…)
Related entries
References
Super-string as a GS-sigma model
A precursor to the actual Green-Schwarz action functional is
-
Michael Green, John Schwarz, Supersymmetrical Dual String Theory, Nucl. Phys. B 181 (1981) 502;
-
Michael Green, John Schwarz, Supersymmetrical Dual String Theory. 2. Vertices and Trees, Nucl. Phys. B 198 (1982) 252.
which presented a light-cone gauge quantization of superstring with manifest target spacetime supersymmetry.
The observation that this has a generally covariant formulation lead to what is now called the Green-Schwarz action functional proper, for the superstring:
-
Michael Green, John Schwarz, Covariant description of superstrings, Phys. Lett. B136 (1984), 367–370 (spire:193596, arXiv;10.1016/0370-2693(84)92021-5)
-
Michael Green, John Schwarz, Properties of the Covariant Formulation of Superstring Theories, Nucl. Phys. B 243 (1984) 285 (spire:196623, doi:10.1016/0550-3213(84)90030-0)
See also the historical comments in
- John Schwarz, slides 24-25 of String Theory in the Twentieth Century, talk at Strings 2016 (pdf)
Early discussion of coupling the GS superstring to general background fields in :
- S. James Gates Jr.: Progress Toward Covariant Formulation of All GS-type -model Actons, in: Superstrings and Particle Theory, Proceedings of the Conference in Tuscaloosa 8–11 November 1989, World Scientific (1990) [doi:10.1142/1051, pdf]
A standard textbook reference for the GS superstring is
- Michael Green, John Schwarz, Edward Witten, volume 1, section 5 of Superstring theory, 3 vols. Cambridge Monographs on Mathematical Physics
and a brief paragraph in Volume II, section 10.2, page 983 of
-
Eric D'Hoker, String theory – lecture 10: Supersymmetry and supergravity , in part 3 of
Pierre Deligne, Pavel Etingof, Dan Freed, L. Jeffrey,
David Kazhdan, John Morgan, D.R. Morrison and Edward Witten, eds. Quantum Fields and Strings, A course for mathematicians, 2 vols. Amer. Math. Soc. Providence 1999. (web version)
Textbook discussion of the Green-Schwarz version of the heterotic string is in
- Leonardo Castellani, Riccardo D'Auria, Pietro Fré, vol 3, section VI.9.7 of Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991)
Comprehensive review:
- Joan Simón, Brane Effective Actions, Kappa-Symmetry and Applications, Living Reviews in Relativity 15 3 (2012) [arXiv:1110.2422, doi:10.12942/lrr-2012-3]
Quantization of the Green-Schwarz string using pure spinors is discussed in
-
Pietro A. Grassi, Giuseppe Policastro, Peter van Nieuwenhuizen, An Introduction to the Covariant Quantization of Superstrings, Class. Quant. Grav. 20 (2003) 395-410 [arXiv:hep-th/0302147]
-
Pietro A. Grassi, Y. Oz, Non-Critical Covariant Superstrings [arXiv:hep-th/0507168]
Review in the superembedding approach
- Dmitri Sorokin, Superbranes and Superembeddings, Phys. Rept. 329 (2000) 1-101 [arXiv:hep-th/9906142]
The observation that the Green-Schwarz action functional is an example of a WZW-model on super-Minkowski spacetime is due to
- Marc Henneaux, Luca Mezincescu, A -Model Interpretation of Green-Schwarz Covariant Superstring Action, Phys. Lett. B 152 (1985) 340 [doi:10.1016/0370-2693(85)90507-6, spire:15922]
For more references on this WZW perspective see below.
For references on curved backgrounds see below.
Super-membrane/M2-brane as a sigma model
The Green-Schwarz sigma-model-type formulation of the super-membrane in 11d (as in the brane scan and in contrast to the black brane-solutions of 11d supergravity) first appears in:
- Eric Bergshoeff, Ergin Sezgin, Paul Townsend: Supermembranes and eleven-dimensional supergravity, Phys. Lett. B 189 (1987) 75-78 [doi:10.1016/0370-2693(87)91272-X, spire:248230]
Via the superembedding approach the equations of motion were obtained in
- Igor Bandos, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Dmitry Volkov, Chapter 3 of Superstrings and supermembranes in the doubly supersymmetric geometrical approach, Nucl. Phys. B446:79-118, 1995 (arXiv:hep-th/9501113)
and the Lagrangian density in:
- Paul Howe, Ergin Sezgin, The supermembrane revisited, Class. Quant. Grav. 22 (2005) 2167-2200 [arXiv:hep-th/0412245, doi:10.1088/0264-9381/22/11/017]
The double dimensional reduction of the M2-brane to the Green-Schwarz superstring was observed in
-
Michael Duff, Paul Howe, T. Inami, Kellogg Stelle, Superstrings in from Supermembranes in , Phys. Lett. B 191 (1987) 70 [doi:10.1016/0370-2693(87)91323-2]
also in: Michael Duff (ed.): The World in Eleven Dimensions 205-206 (1987) [spire:245249]
-
Paul Townsend, The eleven-dimensional supermembrane revisited, Phys. Lett. B 350 (1995) 184-187 [arXiv:hep-th/9501068, doi:10.1016/0370-2693(95)00397-4]
around the time when M-theory became accepted due to
On the early history of these developments:
- Eric A. Bergshoeff, Ergin Sezgin, Paul K. Townsend: A brief history of supermembranes [arXiv:2503.06234]
See also:
-
Igor Bandos, Paul Townsend, SDiff Gauge Theory and the M2 Condensate (arXiv:0808.1583)
-
Maria P. Garcia del Moral, C. Las Heras, P. Leon, J. M. Pena, Alvaro Restuccia, Fluxes, Twisted tori, Monodromy and Supermembranes, J. High Energ. Phys. 2020 97 (2020) [arXiv:2005.06397, doi:10.1007/JHEP09(2020)097]
Discussion from the point of view of Green-Schwarz action functional-∞-Wess-Zumino-Witten theory:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields (2013)
On possible structures in M2-brane dynamics and M2-M5-brane bound states which could be M-theory-lifts of the familiar integrability of the Green-Schwarz superstring on :
- Kirill Gubarev, Edvard Musaev, Integrability structures in string theory [arXiv:2301.06486]
D-branes as GS-sigma models
Green-Schwarz action functionals for the D-branes (including the DBI action):
-
Martin Cederwall, Alexander von Gussich, Bengt Nilsson, Per Sundell, Anders Westerberg, The Dirichlet Super-p-Branes in Ten-Dimensional Type IIA and IIB Supergravity, Nucl.Phys. B490 (1997) 179-201 (arXiv:hep-th/9611159)
-
Mina Aganagic, Jaemo Park, Costin Popescu, John Schwarz, Dual D-Brane Actions, Nucl. Phys. B496 (1997) 215-230 (arXiv:hep-th/9702133)
Dualities
Discussion of T-duality for the Green-Schwarz string is in
-
Mirjam Cvetic, H. Lu, Christopher Pope, Kellogg Stelle, T-Duality in the Green-Schwarz Formalism, and the Massless/Massive IIA Duality Map, Nucl.Phys.B573:149-176,2000 (arXiv:hep-th/9907202)
-
Bogdan Kulik, Radu Roiban, T-duality of the Green-Schwarz superstring, JHEP 0209 (2002) 007 (arXiv:hep-th/0012010)
-
Igor Bandos, Bernard Julia, Superfield T-duality rules, JHEP 0308 (2003) 032 (arXiv:hep-th/0303075)
reviewed in Superfield T-duality rules in ten dimensions with one isometry (arXiv:hep-th/0312299)
WZW terms, super Lie algebra cohomology and the brane scan
The WZW nature of the second term in the GS action, recognized in (Henneaux-Mezincescu 85) is discussed in
-
Jeffrey Rabin: Supermanifold Cohomology and the Wess-Zumino Term of the Covariant Superstring Action, Commun Math. Phys. 108 (1987) 375-389 [euclid:cmp/1104116532]
-
B. Milewski, Superstrings from sigma models, Classical and Quantum Gravity, Volume 4, Number 3 (1987)
-
A.P. Isaev, E.A. Ivanov, On Sigma Model Formulation of Green-Schwarz Superstring, Mod.Phys.Lett. A4 (1989) 351-359 (spire:266793, doi:10.1142/S0217732389000423)
-
José de Azcárraga, Paul Townsend: Superspace geometry and the classification of supersymmetric extended objects, Physical Review Letters 62 22 (1989) [doi:10.1103/PhysRevLett.62.2579, spire:284635]
and with its Lie theoretic meaning made fully explicit (in “FDA” language) in
- José de Azcárraga, José Izquierdo, chapter 8 of Lie Groups, Lie Algebras, Cohomology and Some Applications in Physics, Cambridge monographs of Mathematical Physics (1995) [doi:10.1017/CBO9780511599897]
The original “brane scan” classification of GS action functionals by WZW terms:
- Anna Achúcarro, Jonathan Evans, Paul Townsend, David Wiltshire: Super -Branes, Phys. Lett. B 198 (1987) 441 [spire:22286, doi:10.1016/0370-2693(87)90896-3, pdf, pdf]
A complete rigorous classification of all the relevant cocycles on the super Poincaré Lie algebra was given in
-
Friedemann Brandt, Supersymmetry algebra cohomology
I: Definition and general structure J. Math. Phys.51:122302, 2010, (arXiv:0911.2118)
II: Primitive elements in 2 and 3 dimensions, J. Math. Phys. 51 (2010) 112303 (arXiv:1004.2978)
III: Primitive elements in four and five dimensions, J. Math. Phys. 52:052301, 2011 (arXiv:1005.2102)
IV: Primitive elements in all dimensions from to , J. Math. Phys. 54, 052302 (2013) (arXiv:1303.6211)
For the relevant super Lie algebra cocycles have also been discussed (but not related to the Green-Schwarz action functional) in
- Riccardo D'Auria, Pietro Fré, Geometric Supergravity in D=11 and its hidden supergroup, Nuclear Physics B201 (1982)
A review is in
- Michael Duff, Supermembranes: the first fifteen weeks, Class. Quant. Grav. 5 (1988) 189 [doi:10.1088/0264-9381/5/1/023, spire:248034]
from which the above table is taken.
Systematic review and discussion of the 3- and 4-cocycles in the old brane scan via the relation between division algebras and supersymmetry is in
- John Baez, John Huerta, Division algebras and supersymmetry II, Adv. Math. Theor. Phys. 15 (2011), 1373-1410 (arXiv:1003.34360)
See also
- I. Bars, C. Deliduman and D. Minic, Phys. Rev D59 (1999) 125004; Phys. Lett. B457 (1999) 275. (arXiv:hep-th/9812161)
More along these lines is in
- Michael Duff, S. Ferrara, Four curious supergravities (arXiv)
The Green-Schwarz-type action for the M5-brane was found in
-
Igor Bandos, Kurt Lechner, Alexei Nurmagambetov, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Covariant Action for the Super-Five-Brane of M-Theory (arXiv:hep-th/9701149)
-
Mina Aganagic, Jaemo Park, Costin Popescu, John Schwarz, World-Volume Action of the M Theory Five-Brane (arXiv:hep-th/9701166)
The 7-cocycle on the supergravity Lie 3-algebra which gives the supergravity Lie 6-algebra appears in these articles (somewhat secretly) in equation (BLNPST, equation (9)).
See also
- Igor Bandos, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Superbrane Actions and Geometrical Approach (arXiv:hep-th/9705064)
The 7-cocycle for the M5-brane on the supergravity Lie 3-algebra is equation (8.8) there.
The interpretation of the cocycles for the D-branes and for the M5-brane as cocycles on “extended super-Minkowski spacetime” is due to
-
C. Chryssomalakos, José de Azcárraga, José M. Izquierdo, C. Pérez Bueno, The geometry of branes and extended superspaces, Nucl. Phys. B 567 (2000) 293-330 [arXiv:hep-th/9904137, doi:10.1016/S0550-3213(99)00512-X]
-
Makoto Sakaguchi: IIB-Branes and New Spacetime Superalgebras, JHEP 0004 (2000) 019 [arXiv:hep-th/9909143, doi:10.1088/1126-6708/2000/04/019]
-
José de Azcárraga, J. M. Izquierdo, Superalgebra cohomology, the geometry of extended superspaces and superbranes (arXiv:hep-th/0105125)
See also division algebras and supersymmetry.
A corresponding refinement of the brane scan to a “brane bouquet” of super L-∞ algebra extensions (hence in infinity-Lie theory via ∞-Wess-Zumino-Witten theory) is discussed in
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields, International Journal of Geometric Methods in Modern Physics 12:02 (2015) 1550018 (arXiv:1308.5264)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber The WZW term of the M5-brane and differential cohomotopy, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory and type IIA string theory (arXiv:1606.03206)
-
Vincent Braunack-Mayer, Hisham Sati, Urs Schreiber, Gauge enhancement of Super M-Branes (arXiv:1806.01115)
These cohomological arguments also appear in what is called the “ectoplasm” method for invariants in super Yang-Mills theory in
-
G. Bossard, Paul Howe, K.S. Stelle, A note on the UV behaviour of maximally supersymmetric Yang-Mills theories, Phys. Lett. B682:137-142 (2009) (arXiv:0908.3883)
-
Paul Howe, T. G. Pugh, K. S. Stelle, C. Strickland-Constable, Ectoplasm with an Edge, JHEP 1108:081,2011 (arXiv:1104.4387)
-
G. Bossard, Paul Howe, Ulf Lindström, Kellogg Stelle, L. Wulff, Integral invariants in maximally supersymmetric Yang-Mills theories (arXiv:1012.3142)
The connection is made in
- Paul Howe, O. Raetzel, Ergin Sezgin, On Brane Actions and Superembeddings, JHEP 9808 (1998) 011 (arXiv:hep-th/9804051)
The other brane scan, listing consistent asymptotic AdS/CFT spacetimes/superconformal algebras is due to:
- Miles P. Blencowe, Mike Duff, Supersingletons, Physics letters B, 203 3(1988) 229-236 (cds:184143, doi:10.1016/0370-2693(88)90544-8)
with further developments discussed in
-
Michael Duff, Near-horizon brane-scan revived, Nucl. Phys. B 810:193-209, 2009 (arXiv:0804.3675)
-
Michael Duff, The conformal brane-scan: an update (arXiv:2112.13784)
Anti de Sitter backgrounds
Discussion of Green-Schwarz strings on super anti de Sitter spacetimes includes the following.
General:
-
Machiko Hatsuda, Makoto Sakaguchi, Wess-Zumino term for AdS superstring, Phys.Rev. D66 (2002) 045020 (arXiv:hep-th/0205092, doi:10.1103/PhysRevD.66.045020)
-
Machiko Hatsuda, Makoto Sakaguchi, Wess-Zumino term for the AdS superstring and generalized Inonu-Wigner contraction, Prog.Theor.Phys. 109 (2003) 853-867 (arXiv:hep-th/0106114)
The super 3-cocycle for the Green-Schwarz superstring on the super anti de Sitter spacetime (i.e. on ) is originally due to
- Ruslan Metsaev, Arkady Tseytlin, Type IIB superstring action in background, Nucl. Phys. B533:109-126, 1998 (arXiv:hep-th/9805028)
However, a supersymmetric trivialization of this cocycle seems to have been obtained in
- Radu Roiban, Warren Siegel, Superstrings on supertwistor space, JHEP 0011:024, 2000 (arXiv:hep-th/0010104)
see Hatsuda-Sakaguchi 02, around (1.2) and (2.6), Hatsuda-Sakaguchi 01, around (1.2)
(amplified in arxiv:1808.04470, p. 5 and equation (5.5)).
See also
-
Gleb Arutyunov, Sergey Frolov, Foundations of the Superstring. Part I, J. Phys. A 42 (2009) (arXiv:0901.4937)
-
John Schwarz, The Superstring (arXiv:2004.09661)
and
For the superstring:
-
Gleb Arutyunov, Sergey Frolov, Superstrings on as a Coset Sigma-model, JHEP 0809:129,2008 (arXiv:0806.4940)
-
Pietro Fré, Pietro Antonio Grassi, Pure Spinor Formalism for backgrounds (arXiv:0807.0044)
-
Riccardo D'Auria, Pietro Fré, Pietro Antonio Grassi, Mario Trigiante, Superstrings on from Supergravity (arXiv:0808.1282)
-
D. V. Uvarov, superstring in the light-cone gauge, Nucl.Phys.B826:294-312,2010 (arXiv:0906.4699)
For the M2-brane:
-
Bernard de Wit, Kasper Peeters, Jan Plefka, Alexander Sevrin, The M-Theory Two-Brane in and , Phys.Lett. B443 (1998) 153-158 (arXiv:hep-th/9808052)
-
Makoto Sakaguchi, Hyeonjoon Shin, Kentaroh Yoshida, Semiclassical Analysis of M2-brane in , JHEP 1012:012,2010 (arXiv:1007.3354)
For the M2-brane and the M5-brane:
-
Piet Claus, Super M-brane actions in and , Phys. Rev. D 59 (1999) 066003 [arXiv:hep-th/9809045, doi:10.1103/PhysRevD.59.066003]
-
Makoto Sakaguchi, Kentaroh Yoshida, Open M-branes on Revisited, Nucl.Phys. B714 (2005) 51-66 (arXiv:hep-th/0405109)
Self-dual strings in 6d
Discussion of the self-dual string in 6d as a Green-Schwarz-type sigma model includes
- Par Arvidsson, Erik Flink, Mans Henningson, Supersymmetric coupling of a self-dual string to a tensor multiplet background, JHEP0311:015,2003 (arXiv:hep-th/0309244)
General curved backgrounds and Supergravity background equations of motion
The consistency of the Green-Schwarz action functional for the superstring in a supergravity background should be equivalent to the background satiyfying the supergravity equations of motion. For the superstring this is due to
- Eric Bergshoeff, Ergin Sezgin, Paul Townsend, Superstring actions in curved superspace, Phys.Lett., B169, 191, (1986) (spire)
and for the supermembrane due to
- Eric Bergshoeff, Ergin Sezgin, Paul Townsend, Supermembranes and eleven dimensional supergravity, Phys.Lett. B189 (1987) 75-78, In Mike Duff, (ed.), The World in Eleven Dimensions 69-72 (spire)
with a quick re-derivation using that the torsion constraint in 11d supergravity already imples the sugra equations of motion is in
- Paul Howe, Ergin Sezgin, section 2.1 of The supermembrane revisited, (arXiv:hep-th/0412245)
These authors amplify the role of closed -forms in super -brane backgrounds (p. 3) and clearly state the consistency conditions for the M2-brane in a curved backround in terms of the Bianchi identities on p. 7-8, amounting to the statment that the 4-form field strength has to be the pullback of the cocycle plus the supergravity C-field curvature and has to be closed.
That the heterotic supergravity equations of motion are sufficient for the 3-form super field strength to be closed was first argued in
- Bengt Nilsson, Simple 10-dimensional supergravity in superspace, Nuclear Physics B188 (1981) 176-192 (spire)
and the computation there was highlighted and a little simplified around p. 17 of
- Edward Witten, Twistor-like transform in ten dimensions, Nuclear Physics B266 (1986) (spire)
A more comprehensive result arguing that the heterotic supergravity equations of motion of the background are not just sufficient but also necessary for (and hence equivalent to) the heterotic GS-string on that background being consistent was then claimed in
- Joel Shapiro, Cyrus Taylor, Superspace supergravity from the superstring, Physics letter B 186 1 (1987) [doi:10.1016/0370-2693(87)90514-4]
Discussion of this with the heterotic gauge-field included (hence including the Green-Schwarz anomaly cancellation) is in
- Joseph Atick, Avinash Dhar, Bharat Ratra, Superspace Formulation of Ten-dimensional Supergravity Coupled to Super Yang-Mills Theory, Phys.Rev. D33 (1986) 2824 (spire, pdf)
Similar arguments for the type II string in type II supergravity appeared in
- Marcus Grisaru, Paul Howe, L. Mezincescu, Bengt Nilsson, Paul Townsend, -Superstring in a supergravity background, Physics Letters Volume 162B, number 1,2,3 (1985) (spire)
and for GS sigma-model D-branes in
- Martin Cederwall, Alexander von Gussich, Bengt Nilsson, Per Sundell, Anders Westerberg, The Dirichlet Super-p-Branes in Ten-Dimensional Type IIA and IIB Supergravity, Nucl.Phys. B490 (1997) 179-201 (arXiv:hep-th/9611159)
That the M2-brane sigma-model is consistent on backgrounds of 11-dimensional supergravity that satisfy their equations of motion is discussed in (Bergshoeff-Sezgin-Townsend 87).
The role of the 4-form here is also amplified around (2.29) in
- Igor Bandos, Carlos Meliveo, Supermembrane interaction with dynamical D=4 N=1 supergravity. Superfield Lagrangian description and spacetime equations of motion (arXiv:1205.5885)
and in section 2.2 of
- Igor Bandos, Carlos Meliveo, Three form potential in (special) minimal supergravity superspace and supermembrane supercurrent (arXiv:1107.3232)
following
- Burt Ovrut, Daniel Waldram, Membranes and Three-form Supergravity, Nucl.Phys. B506 (1997) 236-266 (arXiv:hep-th/9704045)
See also
- Bernard de Wit, Kasper Peeters, Jan Plefka, Superspace Geometry for Supermembrane Backgrounds, Nucl.Phys. B532 (1998) 99-123 (arXiv:hep-th/9803209)
All this is actually subsumed by imposing the Bianchi identities of the corresponding supergravity Lie 3-algebra etc. in “rheonomic parameterization”, of the D'Auria-Fré formulation of supergravity, this is discussed in (AFFFTT 98, section 3.1, Fré-Grassi 07).
Discussion including also the RR-field background includes
- R. R. Metsaev, Type IIB Green-Schwarz superstring in plane wave Ramond-Ramond background (arXiv:hep-th/0112044)
Microscopic AdS/CFT via -brane sigma-models
Over a decade before the modern formulation of the AdS-CFT correspondence, a candicate “microscopic” explanation was observed:

Immersing the worldvolume of a sigma-model super -brane (hence a “light” brane without backreaction) along the near horizon geometry (an AdS supergravity solution) of its own black brane incarnation (hence the “heavy” incarnation of the same brane, causing backreaction), its worldvolume fluctuations (after super-diffeomorphism gauge fixing) are described by the corresponding superconformal field theory (exhibited by superconformal multiplets such as “supersingletons”) [graphics from GSS24].
The original observation for the M2-brane:
-
Eric Bergshoeff, Michael Duff, Christopher Pope, Ergin Sezgin: Supersymmetric Supermembrane Vacua and Singletons, Phys. Lett. B 199 (1987) 69-74 [doi:10.1016/0370-2693(87)91465-1, InSpire:250244]
-
Miles P. Blencowe, Mike Duff, Supersingletons, Physics letters B, 203 3 (1988) 229-236 [doi:10.1016/0370-2693(88)90544-8, cds:184143]
-
Gianguido Dall'Agata, Davide Fabbri, Christophe Fraser, Pietro Fré, Piet Termonia, Mario Trigiante, The singleton action from the supermembrane, Nucl. Phys. B 542 (1999) 157-194 [doi:10.1016/S0550-3213(98)00765-2, arXiv:hep-th/9807115]
with popular exposition in:
- Mike Duff, Christine Sutton: The Membrane at the End of the Universe, New Scientist 118 (1988) 67-71 [inspire:268230, ISSN:0028-6664]
Further discussion including also M5-branes and D-branes:
-
Piet Claus, Renata Kallosh, Antoine Van Proeyen, M 5-brane and superconformal tensor multiplet in 6 dimensions, Nucl. Phys. B 518 (1998) 117-150 [doi:10.1016/S0550-3213(98)00137-0, arXiv:hep-th/9711161]
-
Piet Claus, Renata Kallosh, J. Kumar, Paul K. Townsend, Antoine Van Proeyen, Conformal Theory of M2, D3, M5 and “D1+D5” Branes, JHEP 9806 (1998) 004 [doi:10.1088/1126-6708/1998/06/004, arXiv:hep-th/9801206]
-
Paolo Pasti, Dmitri Sorokin, Mario Tonin, Branes in Super-AdS Backgrounds and Superconformal Theories, Proceedings, International Workshop on Supersymmetries and Quantum Symmetries (SQS’99), Moscow (July 27-31, 1999) [arXiv:hep-th/9912076, inspire:511348]
-
C. Grojean, J. Mourad, Super fivebranes near the boundary of , Nuclear Physics B 567 1–2 (2000) 133-150 [doi:10.1016/S0550-3213(99)00335-1, arXiv:hep-th/9903164]
-
Alexei Nurmagambetov, I. Y. Park On the M5 and the correspondence, Physics Letters B
524 1–2 (2002) 185-191 [doi:10.1016/S0370-2693(01)01375-2, arXiv:hep-th/0110192]
Review:
-
Mike Duff, Anti-de Sitter space, branes, singletons, superconformal field theories and all that, Int. J. Mod. Phys. A 14 (1999) 815-844 [doi:10.1142/S0217751X99000403, arXiv:hep-th/9808100]
-
Mike Duff, TASI Lectures on Branes, Black Holes and Anti-de Sitter Space, lectures at 9th CRM Summer School: Theoretical Physics at the End of the 20th Century at TASI 99 (1999) [arXiv:hep-th/9912164, inspire:511822]
The resulting super-conformal brane scan:
-
Michael Duff, Near-horizon brane-scan revived, Nucl. Phys. B 810 (2009) 193-209 [doi:10.1016/j.nuclphysb.2008.11.001, arXiv:0804.3675]
-
Michael Duff, The conformal brane-scan: an update, J. High Energ. Phys. 2022 54 (2022) [doi:10.1007/JHEP06(2022)054, arXiv:2112.13784]
Related:
- Hironori Mori, Satoshi Yamaguchi, §3 in: M5-branes and Wilson Surfaces in AdS7/CFT6 Correspondence, Phys. Rev. D 90 (2014) 026005 [doi:10.1103/PhysRevD.90.026005, arXiv:1404.0930]
Analogous discussion for embeddings with less supersymmetry, corresponding to defects
-
Nadav Drukker, Simone Giombi, Arkady A. Tseytlin, Xinan Zhou, Defect CFT in the 6d theory from M2 brane dynamics in , J. High Energ. Phys. 2020 101 (2020) [doi:10.1007/JHEP07(2020)101, arXiv:2004.04562]
-
Varun Gupta, Holographic M5 branes in , J. High Energ. Phys. 2021 32 (2021) [doi:10.1007/JHEP12(2021)032, arXiv:2109.08551]
-
Varun Gupta, More Holographic M5 branes in , Phys. Lett. B 853 (2024) 138650 [doi:10.1016/j.physletb.2024.138650, arXiv:2301.02528]
Conserved current algebra
That higher WZW functionals and hence Green-Schwarz super -brane action functionals have conserved current BPS charge algebras which are polyvector extensions of the supersymmetry algebras was observed in
- José de Azcárraga, Jerome Gauntlett, J.M. Izquierdo, Paul Townsend, Topological extensions of the supersymmetry algebra for extended objects, Phys. Rev. Lett. 63 (1989) 2443 (spire)
reviewed in
- José de Azcárraga, José M. Izquierdo, section 8.8. of Lie Groups, Lie Algebras, Cohomology and Some Applications in Physics , Cambridge monographs of mathematical physics, (1995)
and generalized to super-Lie n-algebras of BPS charges in
This is for branes in the old brane scan (strings, membranes, NS5-branes), excluding D-branes and M5-brane.
The generalization oft this perspective to the M5-brane is discussed in
- Dmitri Sorokin, Paul Townsend, M-theory superalgebra from the M-5-brane, Phys.Lett. B412 (1997) 265-273 (arXiv:hep-th/9708003)
and the generalizatin to D-branes is discussed in
- Hanno Hammer, Topological Extensions of Noether Charge Algebras carried by D-p-branes, Nucl.Phys. B521 (1998) 503-546 (arXiv:hep-th/9711009)
-Symmetry
The existence of kappa-symmetry was first noticed around
-
Warren Siegel, Hidden Local Supersymmetry In The Supersymmetric Particle Action Phys. Lett. B 128, 397 (1983)
-
Warren Siegel, Light Cone Analysis Of Covariant Superstring , Nucl. Phys. B 236, 311 (1984).
-
Michael Green, John Schwarz, Covariant Description Of Superstrings , Phys. Lett. B 136, 367 (1984) (web)
The meaning of -symmetry in terms of the super-Cartan geometry of super-target space is discussed in
- Ian N. McArthur, Kappa-Symmetry of Green-Schwarz Actions in Coset Superspaces, Nucl. Phys. B 573 (2000) 811-829 [https://doi.org/10.1016/S0550-3213(99)00800-7]
- Joaquim Gomis, Kiyoshi Kamimura, Peter West, Diffeomorphism, kappa transformations and the theory of non-linear realisations (arXiv:hep-th/0607104)
Discussion from the point of view of D'Auria-Fré formulation of supergravity is in
-
Gianguido Dall’Agata, Davide Fabbri, Christophe Fraser, Pietro Fré, Piet Termonia, Mario Trigiante, The singleton action from the supermembrane, Nucl. Phys. B542:157-194,1999, (arXiv:hep-th/9807115)
-
Pietro Fré, Pietro Antonio Grassi, Pure Spinors, Free Differential Algebras, and the Supermembrane, Nucl. Phys. B763:1-34,2007 (arXiv:hep-th/0606171)
Open branes ending on other branes
Discussion of the Green-Schwarz action for the open M2-brane ending on the M5-brane is in
-
C. S. Chu, Ergin Sezgin, M-Fivebrane from the Open Supermembrane, JHEP 9712 (1997) 001 (arXiv:hep-th/9710223)
-
Ph. Brax, J. Mourad, Open Supermembranes Coupled to M-Theory Five-Branes, Phys. Lett. B416 (1998) 295-302 (arXiv:hep-th/9707246)
Last revised on March 25, 2025 at 18:59:02. See the history of this page for a list of all contributions to it.