nLab stratified space
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Contents
Idea
The term stratified space usually refers to a topological space equipped with the structure of a stratification, which decomposes the space into topological subspaces called strata.
Often strata are required to be “nice” in some sense (for instance, one may require strata to be manifolds, while the stratified space itself need not be a manifold), and the way that strata are linked together is typically controlled by additional conditions. More generally, the term “stratified space” may refer to any notion of spaces equipped with some type of stratification structure.
Examples are ubiquitous, canonical stratifications are carried by polyhedra, cell complexes, algebraic varieties, orbit spaces of many group actions on manifolds, mapping cylinders of maps between manifolds, and moduli stacks of formal groups (stratified by height of formal groups).
Variants
There are many different definitions of stratifications on spaces:
-
stratifications from filtrations,
-
Thom-Mather stratifications? (see e.g. Wiki entry),
-
homotopical stratifications (as developed by Quinn),
-
conically smooth stratifications (as developed by Ayala-Francis-Tanaka),
-
etc. …
Basic features
Stratification structures
Most of the above variants share the same basic structure, captured by the following definitions.
Terminology
(exit path preorder)
Given a decomposition of a topological space into connected subspaces (denoted, in the following, by lower-case letters such as ), the exit path preorder of is the preorder of subspaces in with a generating arrow whenever the topological closure of intersects non-trivially.
Definition
A stratification on is a decomposition of such that (Trm. ) is an actual poset.
The subspaces in a stratification are also called strata. The opposite poset is also called the entrance path poset and denoted by .
Remark
(characteristic map)
Given a stratification on , there is a map mapping points to , which is sometimes called the characteristic map of , and (abusing notation) denoted by .
The characteristic map (Rmk. ) need not be continuous in general (unless the stratification is locally finite, see Rmk below); it is, however, continuous on the preimage of any finite full subposet of the exit path poset. It is often convenient to construct stratifications by constructing their characteristic map.
Example
(Stratification of CW complexes)
The following are stratifications of the 1- and 2-spheres: 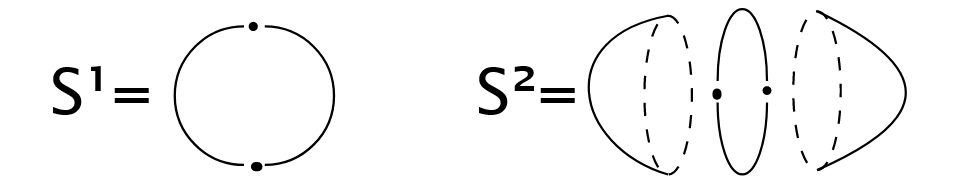
In general, a stratification of a CW complex is obtained by taking the strata to be the -cells of (for each ), but with the -skeleton removed.
Example
(Poset stratifications)
Let be a topological space, a poset, and a continuous map (in other words, is a -stratification of ). This determines a stratification of (in the sense of Def. above) whose strata are the connected components of the preimages , . The map factors uniquely through the characteristic map by a conservative poset map . (Such (characteristic,conservative)-factorizations are essentially unique.)
The example shows that any poset-stratification determines a unique stratification. However, many poset-stratifications may determine the same stratification in this way.
Example
(Filtered spaces) Any filtered topological space in which each is a closed subspace of defines a continuous map mapping points in to , and thus a stratification by Exp. . As a concrete instance of this example, the filtration by skeleta of any cell complex defines the “stratification by cells” in this way.
Example
(Trivial stratification)
Every topological space is trivially stratified (in the sense of Def. ) with strata being the connected components of .
Remark
(Continuity of characteristic map)
Let be a stratified space according to Def. . One says that the stratification is “locally finite” if each stratum of has an open neighborhood in which only contains finitely many strata. (If satisfies the frontier condition (Rmk. below) then, equivalently, is locally finite iff each point has an open neighborhood intersecting only finitely many strata.) If is locally finite, then the characteristic map (Def. ) is a continuous map.
Remark
(Openness of characteristic map)
Let be a stratified space (Def. ). One says the stratification satisfies the “frontier condition” (or, as an adjective, that it is “frontier-constructible”) if, for any two strata , the topological closure intersects non-trivially, then . The stratification is frontier-constructible iff the characteristic map (Def. ) is an open map.
It is generally very reasonable to assume stratifications to be locally finite and frontier-constructible.
The category of stratifications
Definition
A stratified map of stratified spaces (Def. ) is a continuous map which factors through the characteristic maps and (Def. ) by a (then necessarily unique) map, denoted by .
Stratified spaces and their maps (Def. ) form a category of stratification. The construction of exit path posets (Trm. ) yields a functor (dually, using one obtains the entrance path poset functor ). The functor has a right inverse, as follows.
Definition
Every poset has a classifying stratification (also called the stratified realization of ), whose underlying topological space is the classifying space of (i.e. the topological realization of the simplicial nerve of ), and whose characteristic map (Def. ) is the map that maps to (here, the full subposets and of are the “lower” resp. “strict lower closures” of an element in ). Moreover, given a poset map , the realization of its nerve yields a stratified map . We obtain a functor .
Every classifying stratification is frontier-constructible (Rmk. ).
It makes sense to further terminologically distinguish maps of stratifications as follows.
Terminology
(Types of stratified maps)
A stratified map (Def. ) is called:
-
a substratification if is a topological subspace and is conservative; if, moreover, then one says the substratification is constructible;
-
a coarsening if is a homeomorphism (to emphasize the opposite process, one also calls a refinement);
-
a stratified homeomorphism (or stratified iso) if is a homeomorphism of topological spaces and is an isomorphism of posets.
-
a stratified bundle if points for a stratum of admit open neighbourhoods such that, up to stratified iso, restricts on to a projection (see Def. ) for some ‘fiber’ stratification .
Remark
(Constructible bundles). The preceding definition of stratified bundles is rather weak, and in practice one often finds bundles that satisfy stronger conditions, such as constructibility: a constructible stratified bundle is a bundle that, up to bundle isomorphism, can be classified by functorial information associated to the fundamental category (see Def. ) of its stratified base space (cf. Sec. 6.3, Ayala-Francis-Rozenblyum 2015).
Fundamental categories
Just as spaces have fundamental -groupoids, stratified spaces also have “fundamental categories”. However, the role of sets for spaces is now played by posets: the following table illustrates the analogy. (The table is further explained below.)
| base concept | -concept | presentation |
|---|---|---|
| sets -categories | ∞-sets spaces | sets with w.e. |
| posets -categories | ∞-posets stratified spaces | posets with w.e. |
| categories -categories | ∞-categories | categories with w.e. |
In the table, an “-X” is intuitively to be understood as an (∞,∞)-category which admits a conservative functor to an X, where X can e.g. stand for “set”, “poset”, or “category”. Yet more generally, X can be an (n,r)-category for . A “set with weak equivalences” means a poset with weak equivalences in which each arrow is a weak equivalence. The left column is related to the middle column by an “-zation functor” (which simply includes -structures into -structures), and the middle and right columns are related by an “∞-localization functor” (which should be a weak equivalence in some sense).
In order to make the above precise, one must work with sufficiently convenient stratifications. We describe two simple ways of constructing/presenting fundamental -posets below.
For conical stratificiations
Definition
Given stratifications and their product is the stratification of with characteristic map .
Definition
Given a stratification , the stratified (open) cone stratifies the topological open cone by the product away from the cone point (here, the open interval is trivially stratified), and by setting the cone point to be its own stratum.
Definition
A conical stratification is a stratification in which each point has a neighborhood (i.e. an open substratification) that is a stratified product for some “link” stratification and such that .
Every conical stratification is frontier-constructible.
Definition
Given a conical stratification , then Lurie constructs exit path -category as a quasicategory: the -simplices of the quasicategory are precisely stratified maps , where .
Remark
One dually defines the entrance path -category with -simplices .
Terminology
An exit path in a stratified space is a stratified map ; we say starts and ends at (dually, we say is an entrance path which starts at and ends at ).
The construction translates from “stratified spaces” to “-posets” in the above table: the conservative functor takes objects to the stratum that their image lies in.
For regular stratifications
Definition
A stratification is regular if it admits a refinement by the stratified realization of some poset .
Definition
Given a regular stratification and a refinement , one can construct the presented exit path -category as a poset with weak equivalences with underlying poset and weak equivalences .
(Showing that this construction is, in an appropriate sense, independent of the choice of requires a bit more work…)
Remark
A special case of the definition asks for refinements by regular cell complexes (or simplicial complexes) in place of classifying stratifications of posets, in which case one speaks of cellulable (resp. triangulable) stratifications.
The construction translates between “stratified spaces” and “posets with weak equivalences” in the above table. Since spaces are trivially stratified spaces, this specializes to a translation between “spaces” and “sets with weak equivalences”.
Related concepts
References
A notion of purely topologically stratified sets was introduced in
- Frank Quinn, Homotopically stratified sets, J. Amer. Math. Soc. 1 (1988), 441–499. MR 89g:57050
Notions of smoothly stratified spaces were considered by
-
H. Whitney, Local properties of analytic varieties, Differentiable and combinatorial topology (S. Cairns, ed.), Princeton Univ. Press, Princeton, 1965, pp. 205–244. MR 32:5924
-
R. Thom, Ensembles et morphismes stratifiés, Bull. Amer. Math. Soc. 75 (1969), 240–282. MR 39:970
-
J. Mather, Notes on topological stability, Harvard Univ., Cambridge, (1970)
Locally conelike stratified spaces have been considered in
- L. Siebenmann, Deformations of homeomorphisms on stratified sets, Comment. Math. Helv. 47 (1971), 123–165. MR 47:7752
These are all special cases of (Quinn’s definition).
Discussion of differential operators on stratified spaces is in
-
R. B. Melrose, Pseudodifferential operators, corners and singular limits, Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990), 217–234, Math. Soc.
-
Pierre Albin, Eric Leichtnam, Rafe Mazzeo, Paolo Piazza, The signature package on Witt spaces, I. Index classes (arXiv:0906.1568v2)
See also
- Bruce Hughes, Geometric topology of stratified spaces (pdf)
Discussion of the fundamental category of a (Whitney‑)stratified space is in
-
Jonathan Woolf, Transversal homotopy theory [arXiv:0910.3322]
-
Markus Banagl, Topological invariants of stratified spaces, Springer Monographs in Mathematics, Springer (2000) [doi:10.1007/3-540-38587-8]
A homotopy hypothesis for stratified spaces is discussed in
-
David Ayala, John Francis, Nick Rozenblyum, A stratified homotopy hypothesis, arXiv
-
Peter J. Haine, On the homotopy theory of stratified spaces (arXiv:1811.01119)
The former is based on the notion of stratifications developed in
- David Ayala, John Francis, and Hiro Lee Tanaka. Local structures on stratified spaces. Advances in Mathematics 307 (2017): 903-1028.
An earlier paper on exit paths is
- David Treumann, Exit paths and constructible stacks, Compositio Math. 145 (2009), 1504–1532
Poset-stratified spaces and the conicality condition, as well as the construction of the fundamental -poset of a conical stratification as a quasicategory, first appeared in:
- Jacob Lurie, Higher Algebra, 2012, in particular Appendix A (pdf)
Stratified spaces are used to develop a graphical calculus for Gray categories in:
- Benjamin Taylor Hummon, Surface Diagrams for Gray-Categories, PhD thesis.
The homotopy theory of stratified spaces is explored in the thesis of Sylvain Douteau:
- Sylvain Douteau, Étude homotopique des espaces stratifiés, Arxiv version.
Last revised on February 28, 2024 at 13:00:44. See the history of this page for a list of all contributions to it.