Schreiber QS -- Quantum Systems Language

QS is aimed to be a quantum programming language developed at CQTS, the basics of which are now laid out in

The Quantum Monadology [arXiv:2310.15735]:

• A domain specific language,

• for quantum circuits of quantum logic gates

  • with classical control and dynamic lifting.

  • aware of anyonic topological quantum gates (see here),

• naturally embedded into (in fact: “emergent” inside) linear homotopy type theory.

(On the one hand, “QS” is short for Quantum Systems Language; on the other hand, “$Q S$” is a traditional notation for the sphere spectrum (the suspension spectrum $Q$ of the 0-sphere $S^0$), reflecting that linear homotopy type theory is the formal language for $Q S^0$-modules, namely for (parameterized) spectra in the sense of algebraic topology/stable homotopy theory.)

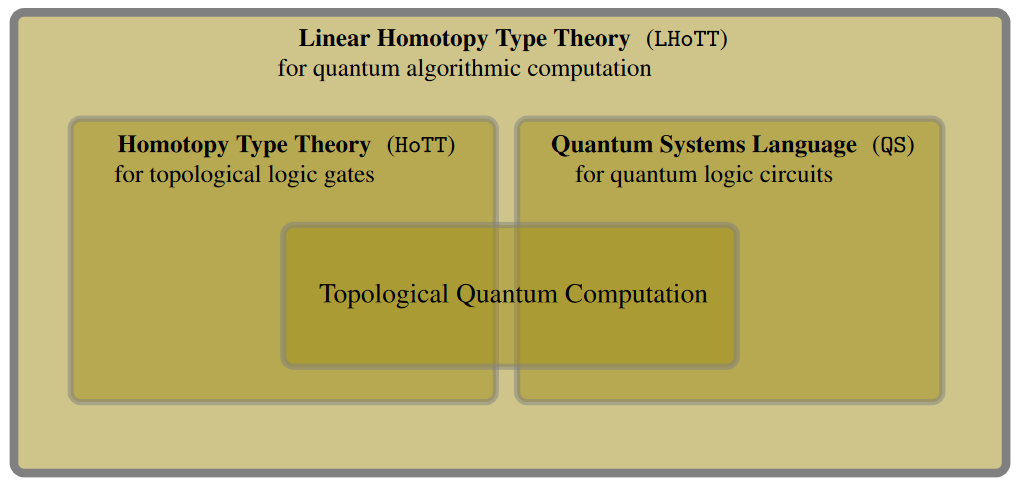
Concretely:

1. Linear homotopy type theory (LHoTT, anticipated by Schreiber (2014) and realized by Riley (2022)) may be regarded as the previously missing ambient algorithmic/universal quantum programming language.

   
   

   (For previous lack of such a universal quantum type theory, existing quantum programming languages are embedded into classical type theories which do not verify the intended quantum semantics: For instance Quipper is embedded into Haskell, and QWIRE is embedded into Coq/classical homotopy type theory.)

2. LHoTT verifies a profound axiom scheme which in its algebro-topological semantics is famous as Grothendieck‘s motivic yoga of six operations (in Wirthmüller's form).

   
   

   (That plain linear type theory expresses unitary/reversible quantum computation has been understood since Pratt (1992) and appreciated since Abramsky & Duncan (2005), but it is the dependency of linear types on classical (“intuitionistic”) types found in linear homotopy type theory which expresses the crucial quantum/classical interaction that is the notoriously subtle core of quantum physics.)

3. The modal type theory of necessity and possibility which is induced by the Motivic Yoga is a domain specific programming language (not just embedded but “emergent” in LHoTT) for quantum circuits with classical control & effects:

   1. the “stability” of linear homotopy types implies that for finite sets of measurement-outcomes (as relevant in quantum information theory), necessity and possibility coincide through a comparison operation reflecting the

      • Gell-Mann principle of quantum physics (“the possible is necessary”)

      and implying that the necessary/possible modes of contingent types are direct sums linearly spanned by the set of classical measurement outcomes, hence that

      • spaces of$\;$ pure quantum states are correctly given by modal linear types;

   2. the (co-)units (return-operations) of the necessity and possibility (co-)monads express exactly the non-unitary quantum gates crossing the quantum/classical divide:

      1. quantum measurement (“the necessary becomes actual”)

      2. quantum state preparation (“the actual is possible”).

   3. the (co-)Kleisli morphisms of these (co-)monads describe

      • quantum logic gates with classical control & effects;

   4. the corresponding string diagrams with respect to the external tensor product on dependent linear types describe exactly the corresponding

      • quantum circuits with classical control & effects.

One finds that in this language $QS$:

1. the equational axioms for quantum programming languages proposed by Staton (2015) are verified, in particular:

   1. the no-cloning theorem is verified;

   2. the deferred measurement principle becomes a verified theorem (namely the Kleisli equivalence for the necessity comonad);

2. “dynamic lifting” (namely of outputs of quantum measurement-gates back into the context) is automatic.

3. The language has sound categorical semantics:

   1. in indexed sets of complex vector spaces (akin to models known for Quipper) capturing the standard semantics of quantum circuit diagrams;

   2. but more generally in the stable homotopy theory of parameterized $H\mathbb{C}$-module spectra,

      where the additional homotopy-theoretic-aspect of the ambient linear homotopy type theory serves to provide another domain specific embedded programming language, this time for topological quantum gates given by anyon braiding,

   3. and yet more generally in in stable homotopy theory of any parameterized (module) spectra,

      where the language specification for anyons further broadens to one for their ambient topologically ordered topological phases of matter,

   thus providing a topological hardware-aware quantum programming language-environment for topological quantum computation, ranging all the way

   • from high-level language constructs for quantum algorithms and quantum circuits:

   • to fine detail of the physical realization of quantum logic gates in quantum materials.

For more see at:

• Topological Quantum Gates in Homotopy Type Theory

• Quantum Certification via Linear Homotopy Types.

Besides these technical properties, the logical language $QS$ is curiously satisfying on quantum-philosophical grounds: For example, the internal language-construct in $QS$ for quantum measurement via the modal logic of necessity is verbatim the same as for classical measurement, only now applied to (dependent) linear types where it happens to imply the collapse of the wavefunction in the categorical semantics. But in the internal logic this effect is just standard conditioning of expectations. In this sense the notorious “measurement problem” of quantum physics disappears when we speak proper $QS$. (This is analogous to what happens internal to proper quantum probability theory, see there.) Moreover, the deferred measurement principle verified in $QS$ implies that even this collapse of the wavefunction in subsystems may be arbitrarily postponed, by observers who have access to the system at large (the “bath”).

---