nLab controlled quantum gate
Context
Computation
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Quantum systems
-
quantum algorithms:
Contents
Idea
In quantum information theory, a controlled quantum gate is a quantum gate whose operation on a given space of states is conditioned on the data in another space of “control states”.
The conceptual problem
The analogous situation for classical logic gates is without subtlety: Here the parameterization of a logic gate on -bits by control bits is a choice of function
from the intended set of controls to the set of functions between the intended input/output; and by the internal hom-adjunction in the cartesian monoidal category of Sets this is in bijective correspondence with a single function out of the Cartesian product set of the control bits with the input bits:
This function would/could be called the “controlled logic gate”. Notice that the control bits in the above function are “discarded after use”, in that they cannot in general be recovered from the output of the above function.
The subtleties with generalizing this situation to quantum logic gates are:
-
The control of quantum gates may be either by quantum data or by classical data, which is not quite the same.
(In a quantum-controlled quantum logic gate, the control itself may be in a quantum superposition, while a classically-controlled quantum gate is effectively an indexed set of quantum gates, indexed by classical data.)
-
A quantum-controlled quantum gate should, like any pure quantum logic gate, be unitary, in particular invertible, hence it “must not discard” its control qbits.
This rules out the otherwise evident non-cartesian analog of the above classical situation (with the product operation replaced by the non-cartesian tensor product of finite-dimensional Hilbert spaces, typically, and hence with the internal hom now being the corresponding linear space of linear maps)):
While the linear map at the bottom always exists, it cannot be invertible (unless the control is trivial, with , or the state space is trivial, with ) and hence does not qualify as a quantum logic gate.
The traditional notion
A general and precise definition of controlled quantum gates is hard to find in traditional literature (cf. Gurevich & Blass (2021) §1).
What traditional texbooks state (e.g. Nielsen & Chuang (2000) §4.3) is that for
a given quantum logic gate, its version controlled by a single qbit is its direct sum with the identity map, which may be thought of as the block-diagonal matrix-notation with diagonal blocks being and the identity function:
If we understand, as usual, that
then this gives a (invertible!) quantum gate on the tensor product space , with the property that
In words: “If the control Qbit is definitely set, then we operate with , if it is definitely not set then we operate trivially, and in general we operate with the respective superposition of these two actions.”
A basic example of this construction is the controlled quantum NOT gate.
Definition
The following is a more general definition along the lines of quantum circuits via dependent linear types.
Given a (finite) set of “control parameter values” (typically Bool = ), a -indexed set of quantum logic gates is a morphism
in a category of -dependent linear types (typically: complex vector bundles over ), which is fiber-wise a linear map with given desired properties (invertible, unitary, …).
As such, we may call this the classically controlled quantum gate, whose classical control parameter is and whose quantum gate action for a given such parameter is .
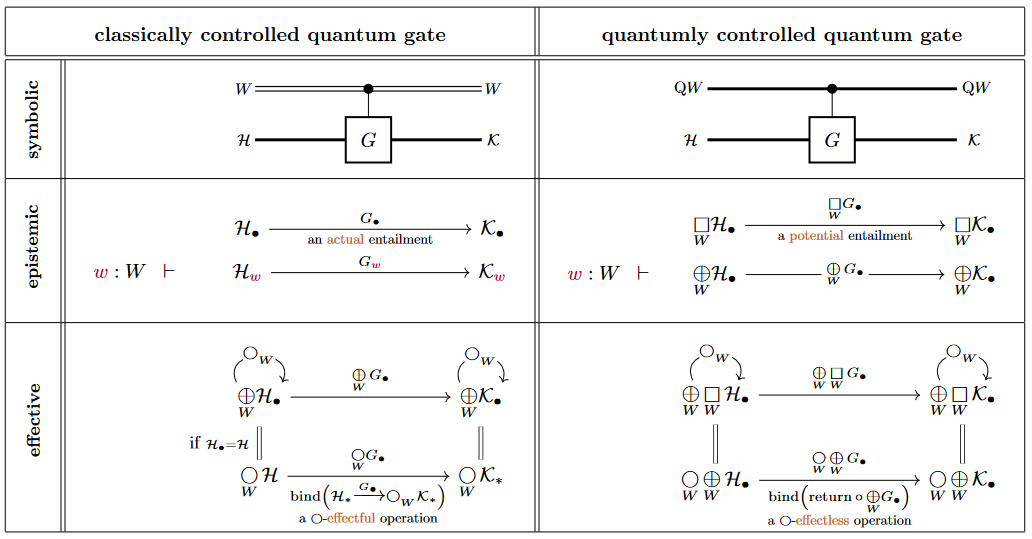
Here in the bottom left we assume that the state spaces themselves are independent of , hence , which is typically the case in application.
Examples
Controlled NOT gate
The following shows the CNOT gate in its two incarnations as a classically or a quantumly controlled quantum gate:
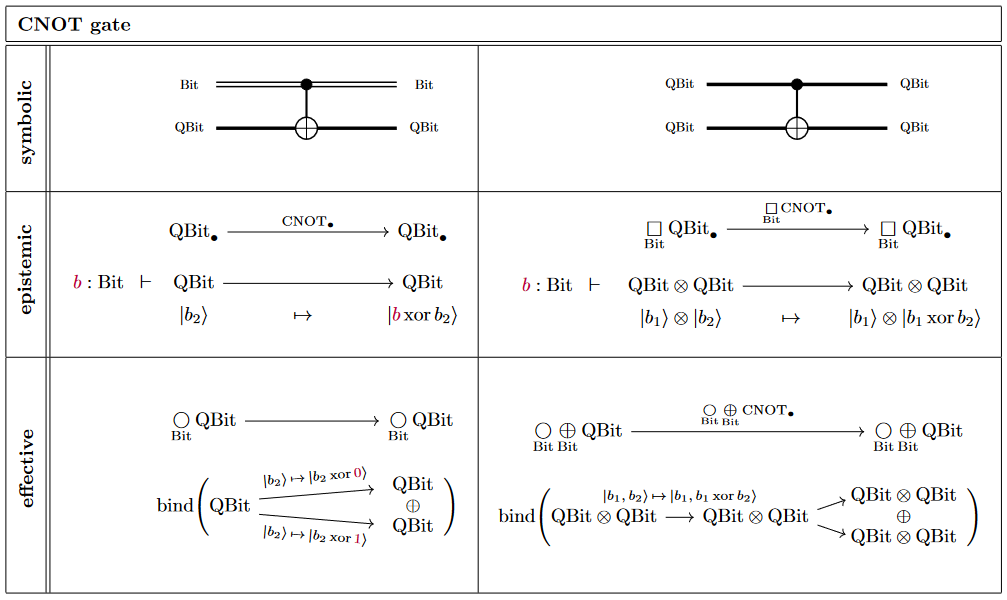
Quantum teleportation
Also the correction-operation in the quantum teleportation protocol (“Bob’s operation”) is given by classically-controlled quantum gates.
Properties
- The deferred measurement principle interchanges classically-controlled with quantumly-controlled quantum gates.
References
The symbolic notation for controlled quantum gates originates with:
-
Richard Feynman, Quantum mechanical computers, Foundations of Physics 16 (1986) 507–531 [doi:10.1007/BF01886518]
-
Adriano Barenco, Charles H. Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, Harald Weinfurter, Elementary gates for quantum computation, Phys. Rev. A52 (1995) 3457 [arXiv:quant-ph/9503016, doi:10.1103/PhysRevA.52.3457]
Traditional textbook accounts of controlled quantum gates:
- Michael A. Nielsen, Isaac L. Chuang, §4.3 Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]
See also at:
Discussion in terms of quantum information theory via dagger-compact categories (cf. at quantum reader monad):
- Chris Heunen, Jamie Vicary, around Lem. 5.61 in: Categories for Quantum Theory, Oxford University Press 2019 ISBN:9780198739616
The above discussion and graphics follows:
- CQTS, Quantum Data Types via Linear HoTT (Nov 2022)
Last revised on February 17, 2025 at 07:11:44. See the history of this page for a list of all contributions to it.