nLab quantum computation
Context
Computation
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Quantum systems
-
quantum algorithms:
Contents
- Idea
- Examples
- Related entries
- References
- General
- Quantum programming languages
- Classically controlled quantum computing
- Noisy intermediate-scale quantum (NISQ) computing
- Quantum programming via monads
- As linear logic
- Quantum information theory via String diagrams
- Topological quantum computing
- Relation to tensor networks
- Spin resonance qbits
- Superconducting qbits
- Photonic qbits
- Commercial quantum computers
Idea
General
Quantum computation is computation in terms of quantum information theory, possibly implemented on quantum computers, hence on physical systems for which phenomena of quantum mechanics are not negligible: quantum systems such as consisting of fundamental particles like photons or electrons but also often of quantum-quasiparticles such as Cooper pairs in superconductors.
In terms of the computational trilogy, quantum computation is the computation corresponding to (some kind of) quantum logic/(dependent) linear type theory.
To the extent that quantum computation involves quantum measurement (generally to read out results, but often also as a kind of quantum logic gate in its own right) it is a form of nondeterministic computation, due to the intrinsic stochastic nature of the quantum state collapse during quantum measurement.
However, away from quantum measurement, quantum gates are understood to implement unitary operators on a given Hilbert space of quantum states (fundamentally due to the unitary nature of time-evolution as given by the Schrödinger equation), for which quantum computation is hence not only deterministic but in fact a form of reversible computation. This relates to its susceptibility to noise and the practical need for quantum error correction and/or topological quantum stabilization.
Specifically, topological quantum computation is (or is meant to be) quantum computation implemented on physical systems governed by topological quantum field theory, such as Chern-Simons theory, thought to describe for instance anyon defects in topologically ordered gapped ground states of quantum materials in topological phases of matter.
Classical control, quantum data
Any practical quantum computer will be classically controlled (an idea that may be traced back to Knill 96, Ömer 03, for more pronounced discussion see Devitt 14).
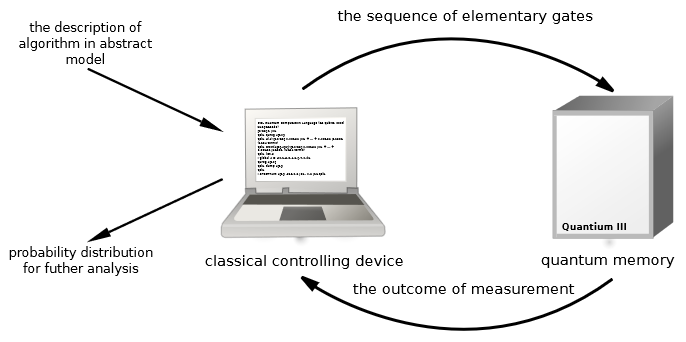
Already for presently available NISQ machines, classically-parameterized quantum systems have been considered in contexts such as quantum machine learning [BLSF 19]:
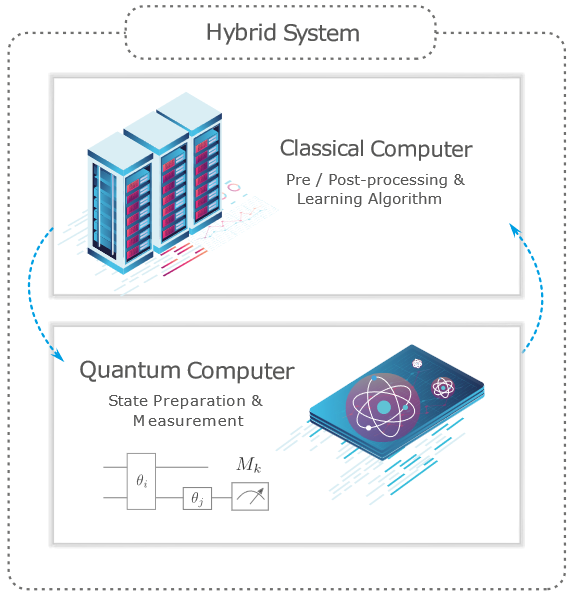
Here the classical control itself is generally conditioned on quantum measurement-outcomes — notably syndrome-measurements for quantum error correction — available only during runtime, a mechanism that in the quantum programming languages-community (Quipper) has come to be called “dynamic lifting”:
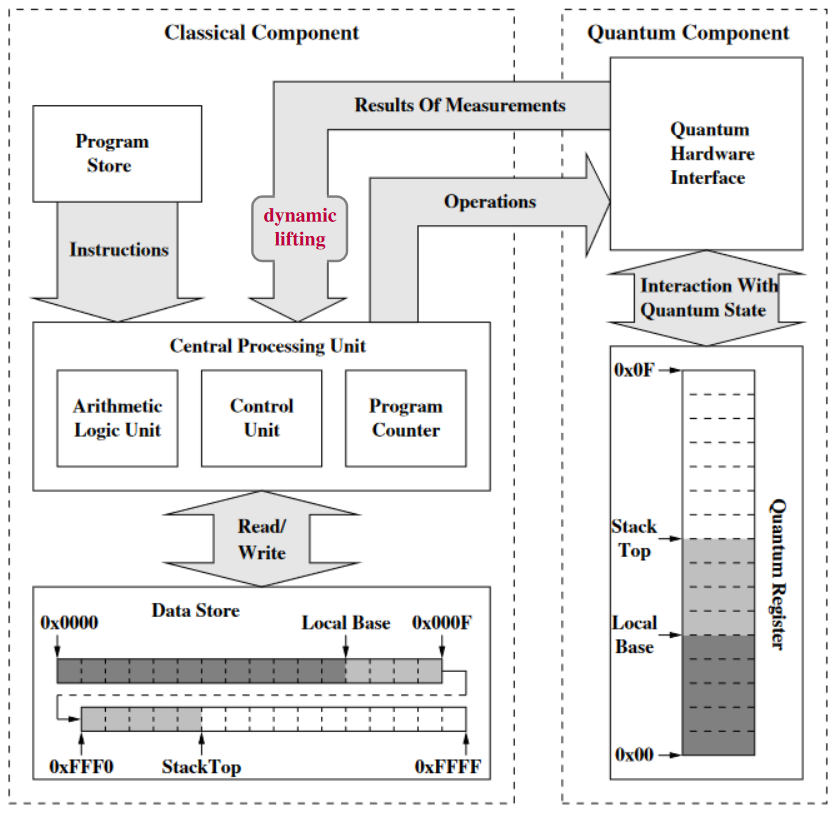
Irrespective of the actual quantum code chosen to protect a quantum computer, it is well known that operating such as system requires extensive classical control infrastructure. This is not simply related to the control of the physical device hardware needed to operate a qubit (lasers, signal generators etc…), but it is also required to decode error correction information produced by the computer.
[KESWDSC 23, p. 2:]
Apart from the requirements on the quantum hardware, the successful execution of QEC codes depends on the classical control system. The classical control system is responsible for all classical aspects of quantum computing and includes executing the quantum control and measurement signals, acquiring the readout signals, and performing classical processing operations, all in a synchronized manner. In QEC, the control system is also responsible for mapping the local physical measurements into logical measurement results or logical Pauli frame updates through an algorithmic procedure called decoding. To reach useful quantum computation with QEC, i.e., perform fault tolerant non-Clifford gates, the control unit is required to perform quantum gates that depend on the decoding output. Moreover, to prevent a diverging classical calculation latency, it is crucial for the control system to close a tight loop, with ultra-low latency, from the physical quantum measurement through the classical decoding procedure to a conditional feed-forward quantum operation. Thus, the success of fault-tolerant quantum computation depends on minimizing the QEC feed-forward latency.
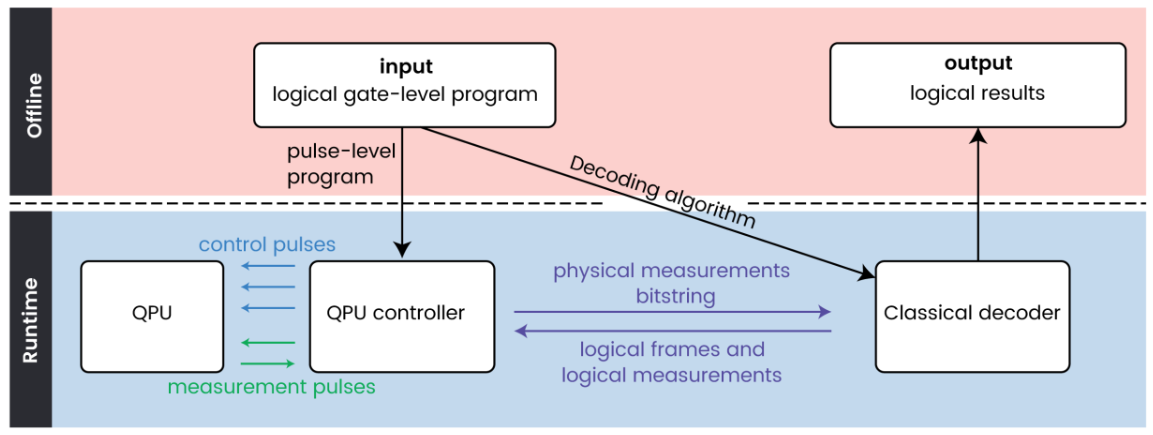
For more on technical details of classical control requirements see also CRKAW 24.
Generally, see the list of references below.
Quantum languages and quantum circuits
A natural way to understand (via computational trilogism) quantum programming languages is as linear logic/linear type theory (Pratt 92, for more see at quantum logic) with categorical semantics in non-cartesian symmetric monoidal categories (Abramsky & Coecke 04, Abramsky & Duncan 05, Duncan 06, Lago-Faffian 12). .
The corresponding string diagrams are known as quantum circuit diagrams.
In fact, languages for classically controlled quantum computation should be based on dependent linear type theory (Vakar 14, Vakar 15, Vakar 17, Sec. 3, Lundfall 17, Lundfall 18, following Schreiber 14) with categorical semantics in indexed monoidal categories:
| classical control | quantum data |
|---|---|
| intuitionistic types | dependent linear types |
This idea of classically controlled quantum programming via dependent linear type theory has been implemented in QML and in Quipper in FKS 20, FKRS 20.
Examples
Related entries
References
General
The idea of quantum computation was first expressed in:
-
Yuri I. Manin, Introduction to: Computable and Uncomputable, Sov. Radio (1980) [Russian original: pdf], Enlish translation on p. 69-77 of Mathematics as Metaphor: Selected essays of Yuri I. Manin, Collected Works 20, AMS (2007) [ISBN:978-0-8218-4331-4]
Perhaps, for a better understanding of [molecular biology], we need a mathematical theory of quantum automata.
-
Paul Benioff, The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines, J Stat Phys 22, 563–591 (1980) [doi:10.1007/BF01011339]
-
Paul Benioff, Quantum Mechanical Models of Turing Machines That Dissipate No Energy, Phys. Rev. Lett. 48 1581 (1982) [doi:10.1103/PhysRevLett.48.1581]
-
Richard Feynman, Simulating physics with computers, Int J Theor Phys 21 (1982) 467–488 [doi:10.1007/BF02650179]
“because nature isn’t classical, dammit, if you want to make a simulation of nature, you’d better make it quantum mechanical”
First ideas of a quantum Turing machine:
-
David Z. Albert, On quantum-mechanical automata, Physics Letters A 98 5–6 (1983) 249-252 [doi:10.1016/0375-9601(83)90863-0]
-
David Deutsch, Quantum theory, the Church–Turing principle and the universal quantum computer, Proceedings of the Royal Society of London A 400 1818 (1985) 97-117 [doi:10.1098/rspa.1985.0070, pdf]
The notion of (controlled) quantum logic gates and quantum circuits was first made explicit in:
-
Richard Feynman, Quantum mechanical computers, Foundations of Physics 16 (1986) 507–531 [doi:10.1007/BF01886518]
-
David E. Deutsch, Quantum computational networks, Proceedings of the Royal Society A, 425 1868 (1989) 73-90 [doi:10.1098/rspa.1989.0099, jstor:2398494]
The terminology q-bit goes back to:
- Benjamin Schumacher, Quantum coding, Phys. Rev. A 51 (1995) 2738 [doi:10.1103/PhysRevA.51.2738]
The potential practical relevance of quantum computation was highlighted early on via toy examples
such as the Deutsch-Jozsa algorithm:
- David Deutsch, Richard Jozsa, Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. A 439 1907 (1992) 553-558 [pdf, doi:10.1098/rspa.1992.0167]
and became widely appreciated in 1996/1997 with the discovery of several practically interesting algorithms exhibiting “quantum supremacy”, such as:
- Seth Lloyd, Universal Quantum Simulators, Science New Series 273 5278 (1996) 1073-1078 [jstor:2899535, doi:10.1126/science.273.5278.1073]
in search algorithms (Grover's algorithm)
- Lov K. Grover, A fast quantum mechanical algorithm for database search, STOC ‘96: Proceedings of the twenty-eighth annual ACM symposium on Theory of Computing (1996) 212-219 [arXiv:quant-ph/9605043, doi:10.1145/237814.237866]
and in (quantum) cryptography (Shor's algorithm)
-
Daniel R. Simon, On the power of quantum computation, SIAM Journal on Computing 26 5 (1997) [doi:10.1137/S0097539796298637, pdf]
-
Peter W. Shor, Algorithms for quantum computation: discrete logarithms and factoring, Proceedings 35th Annual Symposium on Foundations of Computer Science, IEEE Comput. Soc. Press: 124-134 (1994) [doi:10.1109/SFCS.1994.365700]
The first realistic proposal for actually building a quantum gate (namely on trapped ions):
- J. Ignacio Cirac, Peter Zoller: Quantum Computations with Cold Trapped Ions, Phys. Rev. Lett. 74 (1995) 4091 [doi:10.1103/PhysRevLett.74.4091]
Quantum computing became widely thought to be not just a theoretical but a plausible practical possibility with the theoretical understanding of quantum error correction (which however remains to be implemented scalably):
-
Peter W. Shor, Scheme for reducing decoherence in quantum computer memory, Phys. Rev. A 52, R2493(R) 1995 (doi:10.1103/PhysRevA.52.R2493)
-
Andrew M. Steane, Error Correcting Codes in Quantum Theory, Phys. Rev. Lett. 77, 793 1996 (doi:10.1103/PhysRevLett.77.793)
-
Robert Calderbank, Peter W. Shor, Good Quantum Error-Correcting Codes Exist, Phys. Rev. A, Vol. 54, No. 2, pp. 1098-1106, 1996 (doi:10.1103/PhysRevA.54.1098)
and the proof of quantum error threshold theorems:
-
Peter Shor: Fault-tolerant quantum computation, Proceedings of 37th Conference on Foundations of Computer Science (1996) 56-65 [doi:10.1109/SFCS.1996.548464]
-
Emanuel Knill, Raymond Laflamme, Wojciech Zurek: Resilient Quantum Computation: Error Models and Thresholds, Science 279 5349 (1998) 342-345 [doi;10.1126/science.279.5349.342, arXiv:quant-ph/9702058]
-
Dorit Aharonov, Michael Ben-Or: Fault-Tolerant Quantum Computation with Constant Error Rate, SIAM Journal on Computing 38 4 (2008) [doi:10.1137/S0097539799359385, arXiv:quant-ph/9906129]
reviewed in:
- Daniel Gottesman: An Introduction to Quantum Error Correction and Fault-Tolerant Quantum Computation, in: Quantum Information Science and Its Contributions to Mathematics, Proceedings of Symposia in Applied Mathematics 68 (2010) [arXiv:0904.2557, doi:10.1090/psapm/068]
Early review of quantum computing
-
Adriano Barenco, Quantum Physics and Computers, Contemp. Phys. 37 (1996) 375-389 [arXiv:quant-ph/9612014, doi:10.1080/00107519608217543]
-
Yuri I. Manin, Classical computing, quantum computing, and Shor’s factoring algorithm, Astérisque, 266 Séminaire Bourbaki 862 (2000) 375-404 [arXiv:quant-ph/9903008, numdam:SB_1998-1999__41__375_0]
-
T. D. Ladd, F. Jelezko, Raymond Laflamme, Y. Nakamura, C. Monroe & J. L. O’Brien: Quantum computers, Nature 464 (2010) 45–53 [doi:10.1038/nature08812]
Monograph on experimental realizations of quantum gates/quantum computers:
- G. Chen, D. A. Church, B.-G. Englert, C. Henkel, B. Rohwedder, M. O. Scully, S. Zubairy: Quantum Computing Devices – Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]
Review of quantum algorithms:
-
Ashley Montanaro, Quantum algorithms: an overview, npj Quantum Information 2 15023 (2016) [doi:10.1038/npjqi.2015.23]
-
Renato Portugal: Basic Quantum Algorithms [arXiv:2201.10574]
-
Kamil Khadiev: Lecture Notes on Quantum Algorithms [arXiv:2212.14205]
An alternative/parallel approach to avoiding errors due to decoherence is topological quantum computation, see there for references.
Influential list of criteria necessary for physical realization of quantum computation:
- David P. DiVincenzo, The Physical Implementation of Quantum Computation, Fortschr. Phys. 48 9-11 (2000) 771-783 [arXiv:quant-ph/0002077, doi:10.1002/1521-3978(200009)48:9/11%3C771::AID-PROP771%3E3.0.CO;2-E]
Simple quantum computers have been realized (first with NMR technology, see references below, then with superconductor technology, see references further below) and have been argued to demonstrate quantum supremacy (see there for references) but existing machines remain “noisy and intermediate scale” (see the references below).
Textbook accounts on quantum computation:
-
Michael A. Nielsen, Isaac L. Chuang, Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]
-
Samuel J. Lomonaco (ed.), Quantum Computation: A Grand Mathematical Challenge for the Twenty-First Century and the Millennium, Proceedings of Symposia in Applied Mathematics 58, AMS (2002) [doi:10.1090/psapm/058]
-
Alexei Y. Kitaev, A. H. Shen, M. N. Vyalyi, Classical and Quantum Computation, Graduate Studies in Mathematics 47 (2002) [doi:10.1090/gsm/047]
-
Ranee K. Brylinski, Goong Chen (eds.), Mathematics of Quantum Computation, Chapman and Hall/CRC (2002) [doi:10.1201/9781420035377]
-
Giuliano Benenti, Giulio Casati, Davide Rossini, Principles of Quantum Computation and Information, World Scientific (2004, 2018) (doi:10.1142/10909, 2004 pdf)
-
Goong Chen, Louis Kauffman, Samuel J. Lomonaco (eds.), Mathematics of Quantum Computation and Quantum Technology, Chapman and Hall/CRC (2007) [ISBN:9780367388614, doi:10.1201/9781584889007]
-
Eleanor Rieffel, Wolfgang Polak, Quantum Computing – A gentle introduction, MIT Press (2011) [ISBN:9780262526678, pdf]
-
Dirk Bouwmeester, Artur Ekert, Anton Zeilinger (eds.), The Physics of Quantum Information – Quantum Cryptography, Quantum Teleportation, Quantum Computation, Springer (2020) [doi:10.1007/978-3-662-04209-0]
-
Steven Duplij, Raimund Vogl, Innovative Quantum Computing, IOP (2023) [ISBN:978-0-7503-5281-9]
-
Thomas Wong: Intoduction to Classical and Quantum Computing (2024) [pdf, webpage]
-
Rajkumar Buyya, Sukhpal Singh Gill: Quantum Computing – Principles and Paradigms, Elsevier (2025) [ISBN:9780443290961]
Introducing the notion of quantum supremacy and highlighting its relation to quantum entanglement:
- John Preskill: Quantum computing and the entanglement frontier: pp. 63-80 in: The Theory of the Quantum World – Proceedings of the 25th Solvay Conference on Physics, World Scientific (2013) [arXiv:1203.5813, doi:10.1142/8674, slides: pdf]
Further introduction and survey:
-
Alexei Kitaev, Quantum computations: algorithms and error correction, Russian Mathematical Surveys, 52 6 (1997) [doi:10.1070/RM1997v052n06ABEH002155, pdf]
-
Eleanor Rieffel, Wolfgang Polak, An Introduction to Quantum Computing for Non-Physicists, ACM Comput. Surveys 32 (2000) 300-335 [arXiv:quant-ph/9809016, doi:10.1145/367701.367709]
-
John Preskill, Quantum Computation, lecture notes, since 2004 [web]
-
Greg Kuperberg, A concise introduction to quantum probability, quantum mechanics, and quantum computation (2005) [pdf, pdf]
-
Jens Eisert, M. M. Wolf, Quantum computing, In: Handbook of Nature-Inspired and Innovative Computing, Springer 2006 (arXiv:quant-ph/0401019)
-
Scott Aaronson, Quantum Computing Since Democritus, Lecture notes (2006) [web]
-
Phillip Kaye, Raymond Laflamme, Michele Mosca, An Introduction to Quantum Computing, Oxford University Press (2007) [pdf, ISBN:9780198570493]
-
Michael Loceff, A course in quantum computing, 2013 (pdf)
-
Scott Aaronson, Introduction to Quantum Information Science (2018) [pdf, webpage]
Introduction to Quantum Information Science II (2022) [pdf]
-
Emily Grumbling, Mark Horowitz (eds.): Quantum Computing: Progress and Prospects, National Academies of Sciences (2019) [ISBN:9780309479691, doi:10.17226/25196]
-
Qiang Zhang, Feihu Xu, Li Li, Nai-Le Liu, Jian-Wei Pan, Quantum information research in China, Quantum Sci. Technol. 4 040503 (doi:10.1088/2058-9565/ab4bea)
-
Farzan Jazaeri, Arnout Beckers, Armin Tajalli, Jean-Michel Sallese, A Review on Quantum Computing: Qubits, Cryogenic Electronics and Cryogenic MOSFET Physics, 2019 MIXDES - 26th International Conference “Mixed Design of Integrated Circuits and Systems” (2019) 15-25 [arXiv:1908.02656, doi:10.23919/MIXDES.2019.8787164]
-
Melanie Swan, Renato P dos Santos, Frank Witte, Between Science and Economics, Volume 2: Quantum Computing Physics, Blockchains, and Deep Learning Smart Networks, World Scientific 2020 (doi:10.1142/q0243)
-
Jiajun Chen, Review on Quantum Communication and Quantum Computation, Journal of Physics: Conference Series, Volume 1865, 2021 International Conference on Advances in Optics and Computational Sciences (ICAOCS) 2021 21-23 January 2021, Ottawa, Canada (doi:10.1088/1742-6596/1865/2/022008)
-
David Matthews, How to get started in quantum computing, Nature 591 March 2021 (nature:d41586-021-00533-x, pdf)
-
Christine Middleton, What’s under the hood of a quantum computer?, Physics Today, March 2021 (doi:10.1063/PT.6.1.20210305a)
-
John Preskill, The Physics of Quantum Information, talk at The Physics of Quantum Information, 28th Solvay Conference on Physics (2022) [arXiv:2208.08064]
-
Oswaldo Zapata, A Short Introduction to Quantum Computing for Physicists [arXiv:2306.09388]
-
Peter Shor, Quantum Computation, Lecture notes (2022) [web]
-
Anton Frisk et al., Lecture notes on quantum computing [arXiv:2311.08445]
-
I. I. Beterov: Progress and Prospects in the Field of Quantum Computing, Optoelectron. Instrument. Proc. 60 (2024) 74–83 [doi:10.3103/S8756699024700043]
-
Robert Kudelić: On the Theory of Quantum and Towards Practical Computation, Journal of Computational Science 83 (2024) 102454 [arXiv:2403.09682, doi:10.1016/j.jocs.2024.102454]
On “continuous variable” analog quantum computation:
-
Sophie Choe, Quantum computing overview: discrete vs. continuous variable models [arXiv:2206.07246]
-
Vivien M. Kendon, Kae Nemoto, William J. Munro, Quantum Analogue Computing, Phil. Trans. R. Soc. A 368 1924 (2010) 3621-3632 [arXiv:1001.2215, doi:10.1098/rsta.2010.0017]
See also:
-
Wikipedia, Quantum computation
-
Quantiki – Quantum Information Portal and Wiki
-
idquantique, Quantum Computing Review:
Experimental demonstration of “quantum supremacy” (“quantum advantage”):
-
F. Arute et al. Quantum supremacy using a programmable superconducting processor, Nature 574 (2019) 505–510 (doi:10.1038/s41586-019-1666-5)
-
Han-Sen Zhong et al., Quantum computational advantage using photons, Science 370 6523 (2020) 1460-1463 (doi:10.1126/science.abe8770)
Review:
-
Adrian Cho, Google claims quantum computing milestone, Science 365 6460 (2019) 1364 (doi:10.1126/science.365.6460.1364)
-
Philip Ball, Physicists in China challenge Google’s “quantum advantage”, Nature 588 380 (2020) (doi:10.1038/d41586-020-03434-7)
-
Sankar Das Sarma, Quantum computing has a hype problem, MIT Technology Review (March 2022)
The qubit systems we have today are a tremendous scientific achievement, but they take us no closer to having a quantum computer that can solve a problem that anybody cares about. What is missing is the breakthrough bypassing quantum error correction by using far-more-stable qubits, in an approach called topological quantum computing.
Potential relation to the Unruh effect:
- Eric W. Aspling, John A. Marohn, Michael J. Lawler, Design Constraints for Unruh-DeWitt Quantum Computers [arXiv:2210.12552]
Quantum programming languages
The first proposal towards formalizing quantum programming languages was:
- Emanuel Knill, Conventions for quantum pseudocode, Los Alamos Technical Report (1996) LA-UR-96-2724, doi:10.2172/366453, pdf, pdf
and early formalization via quantum lambda-calculus invoking linear logic/linear types (cf. Pratt 1992 etc.):
-
Benoît Valiron, A functional programming language for quantum computation with classical control, MSc thesis, University of Ottawa (2004) doi:10.20381/ruor-18372, pdf
-
Peter Selinger, Benoît Valiron, A lambda calculus for quantum computation with classical control, Proc. of TLCA 2005 arXiv:cs/0404056, doi:10.1007/11417170_26
-
Peter Selinger, Benoît Valiron, Quantum Lambda Calculus, in: Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 135-172 doi:10.1017/CBO9781139193313.005, pdf
[Selinger (2016):] When the QPL workshop series was first founded, it was called “Quantum Programming Languages”. One year I wasn’t participating, and while I wasn’t looking they changed the name to “Quantum Physics and Logic” — same acronym!
Back in those days in the early 21st century we were actually trying to do programming languages for quantum computing Selinger & Valiron 2004, but the sad thing is: In those days nobody really cared.
Now it’s 15 years later and several of these parameters have changed: There has been a renewed interest, from government agencies and also from companies who are actually building quantum computers. .
So now people are working on quantum programming languages again.
Exposition of the general idea of quantum programming languages for classically controlled quantum computation with an eye towards the Quipper-language:
- Benoît Valiron, Neil J. Ross, Peter Selinger, D. Scott Alexander, Jonathan M. Smith, Programming the quantum future, Communications of the ACM 58 8 (2015) 52–61 doi:10.1145/2699415, pdf, web, promo vid:YT
On quantum programming languages (programming languages for quantum computation):
General:
-
Jarosław Adam Miszczak, Models of quantum computation and quantum programming languages, Bull. Pol. Acad. Sci.-Tech. Sci., Vol. 59, No. 3 (2011), pp. 305-324 (arXiv:1012.6035)
-
Jarosław Adam Miszczak, High-level Structures for Quantum Computing, Morgan&Claypool 2012 (doi:10.2200/S00422ED1V01Y201205QMC006, pdf)
See also:
- Wikipedia, Quantum programming
Surveys of existing languages:
-
Simon Gay, Quantum programming languages: Survey and bibliography, Mathematical Structures in Computer Science16(2006) (doi:10.1017/S0960129506005378, pdf)
-
Sunita Garhwal, Maryam Ghorani , Amir Ahmad, Quantum Programming Language: A Systematic Review of Research Topic and Top Cited Languages, Arch Computat Methods Eng 28, 289–310 (2021) (doi:10.1007/s11831-019-09372-6)
-
B. Heim et al., Quantum programming languages, Nat Rev Phys 2 (2020) 709–722 doi:10.1038/s42254-020-00245-7
Quantum programming via quantum logic understood as linear type theory interpreted in symmetric monoidal categories:
-
Vaughan Pratt, Linear logic for generalized quantum mechanics, in Proc. of Workshop on Physics and Computation (PhysComp’92), Dallas (1992) pdf, Pratt-LinearLogic.pdf, web
-
Samson Abramsky, Bob Coecke, A categorical semantics of quantum protocols , Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) (arXiv:quant-ph/0402130)
-
Samson Abramsky, Ross Duncan, A Categorical Quantum Logic, Mathematical Structures in Computer Science, 16 3 (2006) 469-489 arXiv:quant-ph/0512114, doi:10.1017/S0960129506005275
-
Ross Duncan, Types for Quantum Computing, (2006) pdf
-
Ugo Dal Lago, Claudia Faggian, On Multiplicative Linear Logic, Modality and Quantum Circuits, EPTCS 95 (2012) 55-66 arXiv:1210.0613, doi:10.4204/EPTCS.95.6
-
Sam Staton, Algebraic Effects, Linearity, and Quantum Programming Languages, POPL ‘15: Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (2015) doi:10.1145/2676726.2676999, pdf
“A quantum programming language captures the ideas of quantum computation in a linear type theory.”
The corresponding string diagrams are known in quantum computation as quantum circuit diagrams:
-
Giuliano Benenti, Giulio Casati, Davide Rossini, Chapter 3 of: Principles of Quantum Computation and Information, World Scientific 2018 (doi:10.1142/10909, 2004 pdf)
Typedfunctional programming languages for quantum computation:
QPL:
- Peter Selinger, Towards a quantum programming language, Mathematical Structures in Computer Science 14 4 (2004) 527–586 doi:10.1017/S0960129504004256, pdf, web
QML:
-
Thorsten Altenkirch, Jonathan Grattage, A functional quantum programming language, Logic in Computer Science, 2005. Proceedings. 20th Annual IEEE Symposium on, 26-29 June 2005 Page(s):249 - 258 (arXiv:quant-ph/0409065, doi:10.1109/LICS.2005.1, pdf)
-
Jonathan Grattage, An overview of QML with a concrete implementation in Haskell, talk at Quantum Physics and Logic 2008, ENTCS: Proceedings of QPL V - DCV IV, 157-165, Reykjavik, Iceland, 2008 (arXiv:0806.2735)
- Thorsten Altenkirch, Alexander Green, The quantum IO monad, Ch. 5 of: Simon Gay, Ian Mackie (eds.): Semantic Techniques in Quantum Computation (2010) 173-205 pdf, doi:10.1017/CBO9781139193313.006
-
Peter Selinger, The Quipper Language (web)
-
Alexander Green, Peter LeFanu Lumsdaine, Neil Ross, Peter Selinger, Benoît Valiron, Quipper: A Scalable Quantum Programming Language, ACM SIGPLAN Notices 48 6 (2013) 333-342 arXiv:1304.3390
-
Alexander Green, Peter LeFanu Lumsdaine, Neil Ross, Peter Selinger, Benoît Valiron, An Introduction to Quantum Programming in Quipper, Lecture Notes in Computer Science 7948:110-124, Springer, 2013 (arXiv:1304.5485)
-
Jonathan Smith, Neil Ross, Peter Selinger, Benoît Valiron, Quipper: Concrete Resource Estimation in Quantum Algorithms, QAPL 2014 (arXiv:1412.0625)
-
Francisco Rios, Peter Selinger, A Categorical Model for a Quantum Circuit Description Language, EPTCS 266, 2018, pp. 164-178 (arXiv:1706.02630)
-
Jennifer Paykin, Robert Rand, Steve Zdancewic, QWIRE: a core language for quantum circuits, POPL 2017: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages (2017) 846–858 (doi:10.1145/3009837.3009894)
(using the exponential modality between linear type theory and intuitionistic type theory)
-
Jennifer Paykin, Linear/non-Linear Types For Embedded Domain-Specific Languages, 2018 (upenn:2752)
-
Jennifer Paykin, Steve Zdancewic, A HoTT Quantum Equational Theory, talk at QPL2019 arXiv:1904.04371, talk slides: pdf, pdf
(using ambient homotopy type theory)
CoqQ:
- Li Zhou, Gilles Barthe, Pierre-Yves Strub, Junyi Liu, Mingsheng Ying, CoqQ: Foundational Verification of Quantum Programs arXiv:2207.11350
On Q Sharp:
- Kartik Singhal, Kesha Hietala, Sarah Marshall, Robert Rand, Q# as a Quantum Algorithmic Language, Proceedings of Quantum Physics and Logic (2022) arXiv:2206.03532
On classically controlled quantum computation:
- Bernhard Ömer, Structured Quantum Programming, 2003/2009 (pdf)
Quantum programming via dependent linear type theory/indexed monoidal (∞,1)-categories:
-
Urs Schreiber, Quantization via Linear Homotopy Types (arXiv:1402.7041)
-
Peng Fu, Kohei Kishida, Peter Selinger, Linear Dependent Type Theory for Quantum Programming Languages, LICS ‘20: Proceedings of the 35th Annual ACM/IEEE Symposium on Logic in Computer ScienceJuly 2020 Pages 440–453 (arXiv:2004.13472, doi:10.1145/3373718.3394765, pdf, video)
specifically with Quipper:
- Peng Fu, Kohei Kishida, Neil Ross, Peter Selinger, A Tutorial Introduction to Quantum Circuit Programming in Dependently Typed Proto-Quipper, in I. Lanese, M. Rawski (eds.) Reversible Computation RC 2020. Lecture Notes in Computer Science, vol 12227 (arXiv:2005.08396, doi:10.1007/978-3-030-52482-1_9)
See also QS.
On quantum software engineering:
- Manuel A. Serrano, Ricardo Pérez-Castillo, Mario Piattini, Quantum Software Engineering, Springer (2022) doi:10.1007/978-3-031-05324-5
with QWIRE:
-
Robert Rand, Jennifer Paykin, Steve Zdancewic, QWIRE Practice: Formal Verification of Quantum Circuits in Coq, EPTCS 266, 2018, pp. 119-132 (arXiv:1803.00699)
-
Robert Rand, Jennifer Paykin, Dong-Ho Lee, Steve Zdancewic, ReQWIRE: Reasoning about Reversible Quantum Circuits, EPTCS 287 (2019) 299-312 arXiv:1901.10118, doi:10.4204/EPTCS.287.17
- Linda Anticoli, Carla Piazza, Leonardo Taglialegne, Paolo Zuliani, Towards Quantum Programs Verification: From Quipper Circuits to QPMC, In: Devitt S., Lanese I. (eds.) Reversible Computation. RC 2016, Lecture Notes in Computer Science 9720 Springer (2016) arXiv:1708.06312, doi:10.1007/978-3-319-40578-0_16
with CoqQ: Ying et al. (2022)
with QBricks:
- Christophe Chareton, Sébastien Bardin, François Bobot, Valentin Perrelle, Benoit Valiron: A Deductive Verification Framework for Circuit-building Quantum Programs, in: Programming Languages and Systems. ESOP 2021, Lecture Notes in Computer Science 12648, Springer (2021) [doi:10.1007/978-3-030-72019-3_6, arXiv:2003.05841, pdf]
Classically controlled quantum computing
Theory of classically controlled quantum computing and parameterized quantum circuits:
-
Emanuel Knill, Conventions for quantum pseudocode, Los Alamos Technical Report (1996) [LA-UR-96-2724, doi:10.2172/366453, pdf]
-
Bernhard Ömer, Structured Quantum Programming, 2003/2009 (pdf)
-
Simon Perdrix, Philippe Jorrand, Classically-Controlled Quantum Computation, Math. Struct. in Comp. Science, 16:601-620, 2006 (arXiv:quant-ph/0407008)
-
Rajagopal Nagarajan, Nikolaos Papanikolaou, David Williams, Simulating and Compiling Code for the Sequential Quantum Random Access Machine, Electronic Notes in Theoretical Computer Science Volume 170, 6 March 2007, Pages 101-124 (doi:10.1016/j.entcs.2006.12.014)
-
Jarosław Adam Miszczak, Models of quantum computation and quantum programming languages, Bull. Pol. Acad. Sci.-Tech. Sci., Vol. 59, No. 3 (2011), pp. 305-324 (arXiv:1012.6035)
-
Simon J. Devitt, Classical Control of Large-Scale Quantum Computers, In: S. Yamashita, S. Minato (eds.) Reversible Computation Lecture Notes in Computer Science 8507, Springer (2014) [arXiv:1405.4943, doi:10.1007/978-3-319-08494-7_3]
-
Jarrod R McClean, Jonathan Romero, Ryan Babbush and Alán Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, New Journal of Physics, Volume 18, February 2016 (doi:10.1088/1367-2630/18/2/023023)
-
Murray Thom (D-Wave), Three Truths and the Advent of Hybrid Quantum Computing (Jun 25, 2019)
-
Yaniv Kurman, Lior Ella, Ramon Szmuk, Oded Wertheim, Benedikt Dorschner, Sam Stanwyck, Yonatan Cohen: Control Requirements and Benchmarks for Quantum Error Correction [arXiv:2311.07121]
-
Daan Camps, Ermal Rrapaj, Katherine Klymko, Brian Austin, Nicholas J. Wright: Evaluation of the Classical Hardware Requirements for Large-Scale Quantum Computations, ISC High Performance 2024 Research Paper Proceedings (39th International Conference), Hamburg, Germany (2024) 1-12 [doi:10.23919/ISC.2024.10528937]
Application of classically controlled quantum computation:
-
Isaac H. Kim, Brian Swingle, Robust entanglement renormalization on a noisy quantum computer (arXiv:1711.07500)
(in terms of holographic tensor network states)
-
Sukin Sim, Peter D. Johnson, Alan Aspuru-Guzik, Expressibility and entangling capability of parameterized quantum circuits for hybrid quantum-classical algorithms, Adv. Quantum Technol. 2 (2019) 1900070 (arXiv:1905.10876)
-
Mateusz Ostaszewski, Edward Grant, Marcello Benedetti, Structure optimization for parameterized quantum circuits, Quantum 5, 391 (2021) (arXiv:1905.09692)
-
Ruslan Shaydulin et al., A Hybrid Approach for Solving Optimization Problems on Small Quantum Computers (doi:10.1109/MC.2019.2908942)
-
Eneko Osaba, Esther Villar-Rodriguez, Izaskun Oregi, Aitor Moreno-Fernandez-de-Leceta, Focusing on the Hybrid Quantum Computing – Tabu Search Algorithm: new results on the Asymmetric Salesman Problem (arXiv:2102.05919)
in particular in quantum machine learning:
-
Marcello Benedetti, Erika Lloyd, Stefan Sack, Mattia Fiorentini, Parameterized quantum circuits as machine learning models, Quantum Science and Technology 4 043001 (2019) [arXiv:1906.07682]
-
D. Zhu et al. Training of quantum circuits on a hybrid quantum computer, Science Advances, 18 Oct 2019: Vol. 5, no. 10, eaaw9918 (doi: 10.1126/sciadv.aaw9918)
-
Andrea Mari, Thomas R. Bromley, Josh Izaac, Maria Schuld, Nathan Killoran, Transfer learning in hybrid classical-quantum neural networks, Quantum 4, 340 (2020) (arXiv:1912.08278)
-
Thomas Hubregtsen, Josef Pichlmeier, Patrick Stecher, Koen Bertels, Evaluation of Parameterized Quantum Circuits: on the relation between classification accuracy, expressibility and entangling capability, Quantum Machine Intelligence volume 3, Article number: 9 (2021) (arXiv:2003.09887, doi:10.1007/s42484-021-00038-w)
Noisy intermediate-scale quantum (NISQ) computing
The origin of the notion:
-
Nikolaj Moll et al., Quantum optimization using variational algorithms on near-term quantum devices, Quantum Science and Technology 3 3 (2018) &lbrackarXiv:1710.01022, doi:10.1088/2058-9565/aab822]
-
John Preskill, Quantum Computing in the NISQ era and beyond, Quantum 2 79 (2018) [arXiv:1801.00862, doi:10.22331/q-2018-08-06-79]
On the limitations of (quantum error-corrected) NISQ machines in achieving any quantum advantage:
-
Subhash Kak: Prospects for Quantum Computing, talk at CIFAR Nanotechnology program meeting, Halifax (November 2008) [arXiv:0902.4884]
-
Mikhail Dyakonov: Prospects for quantum computing: extremely doubtful, Int. J. of Modern Physics: Conf. Series 33 (2014) 1460357 [arXiv:1401.3629, doi:10.1142/S2010194514603573]
-
Gil Kalai: The Argument against Quantum Computers, in: Quantum, Probability, Logic – The Work and Influence of Itamar Pitowsky, Springer (2020) 399-422 [arXiv:1908.02499, doi:10.1007/978-3-030-34316-3_18]
A common interpretation of the threshold theorem is that it shows that large-scale quantum computers are possible in principle. A more careful interpretation is that if we can control noisy intermediate-scale quantum systems well enough, then we can build large-scale universal quantum computers. As we will see, there are good reasons for why we cannot control the quality of noisy intermediate-scale quantum systems well enough.
-
Daniel Koch, Brett Martin, Saahil Patel, Laura Wessing, and Paul M. Alsing, Demonstrating NISQ era challenges in algorithm design on IBM’s 20 qubit quantum computer, AIP Advances 10 095101 (2020) [doi:10.1063/5.0015526]
-
Frank Leymann, Johanna Barzen, The bitter truth about gate-based quantum algorithms in the NISQ era, Quantum Sci. Technol. 5 044007 (2020) [doi:10.1088/2058-9565/abae7d]
-
Mikhail Dyakonov: Will We Ever Have a Quantum Computer, Springer Briefs in Physics, Springer (2020) [doi:10.1007/978-3-030-42019-2, pdf]
(the author’s conclusion is: “No.”)
-
Olivier Ezratty, Where are we heading with NISQ? [arXiv:2305.09518, InSpire:2660378]
“no one has yet successfully implemented a use case matching the original definition of the NISQ regime.”
“Totally outside the NISQ relevant algorithms class are integer and discrete log factoring algorithms [Shor's algorithm], oracle based search algorithms [Grover's algorithm], and all algorithms relying on a quantum Fourier transform”
“most NISQ experiments have been run with fewer than 30 qubits and should therefore better be labelled as “pre-NISQ”. While they are elegant proofs of concepts, they do not yet demonstrate any speed up over classical computing”
-
Olivier Ezratty, Where are we heading with NISQ?, blog post (2023) [web, pdf]
NISQ is not at all ready for prime time quantum computing despite all the fuss about “quantum computing being business ready”. Not only have we not yet reached any quantum computing advantage, but in many cases, even if it worked, the most common NISQ algorithms using a variational approach, have prohibitively long execution times particularly in the promising chemical simulations domain.
-
Jonathan Wei Zhong Lau, Kian Hwee Lim, Harshank Shrotriya, Leong Chuan Kwek, NISQ computing: where are we and where do we go?, AAPPS Bull. 32 27 (2022) [doi:10.1007/s43673-022-00058-z]
However, quantum computers are still far from achieving all that they have promised. While early-stage quantum computers have been developed, the problems of noisy calculations and scalability of quantum computers still plague the field. As opposed to the far future, where quantum computers can be as big as we wish them to be and are capable of performing fully controllable operations (termed as the fault-tolerant era), we are currently working in the Noisy Intermediate-Scale Quantum (NISQ) era, which is an operational definition that implies that the quantum computers available to us now are subject to substantial error rates and they are constrained in size (in terms of the number of qubits). While it is already a scientific achievement to get to this stage, such quantum computers are still incapable of showing any significant advantages over classical computers. As such, some people in the community have already expressed fear that there will be a ‘Quantum winter’, or a scenario where quantum computing devices remain noisy and are unable to scale up in terms of qubit size, preventing us from ever achieving a meaningful advantage over classical computers.
-
John Preskill, Crossing the Quantum Chasm: From NISQ to Fault Tolerance, talk at Q2B 2023 Silicon Valley (2023) [pdf, pdf]
“there is no proposed application of NISQ computing with commercial value for which quantum advantage has been demonstrated”
“Nor are there persuasive theoretical arguments indicating that commercially viable applications will be found that do not use quantum error-correcting codes and fault-tolerant quantum computing.”
-
Torsten Hoefler, Thomas Haener, Matthias Troyer, Disentangling Hype from Practicality: On Realistically Achieving Quantum Advantage, Communications of the ACM 66 5 (May 2023) 82-87 [arXiv:2307.00523, acm pdf, doi:10.1145/3571725]
“A large range of problem areas with quadratic quantum speedups, such as many current machine learning training approaches, accelerating drug design and protein folding with Grover’s algorithm, speeding up Monte Carlo simulations through quantum walks, as well as more traditional scientific computing simulations including the solution of many non-linear systems of equations, such as fluid dynamics in the turbulent regime, weather, and climate simulations will not achieve quantum advantage with current quantum algorithms in the foreseeable future.”
-
Edd Gent: Quantum Computing’s Hard, Cold Reality Check, IEEE Spectrum (Dec. 2023) [webpage]
-
Xavier Waintal: The Quantum House Of Cards, PNAS 121 1 (2024) e2313269120 [doi:10.1073/pnas.2313269120, arXiv:2312.17570]
On the resulting drop in investment:
- James McKenzie: Quantum winter? No chance!, Physics World, 37 5 (2024) 41 [doi:10.1088/2058-7058/37/05/32]
More optimistic outlook:
-
S. G. Gill et al.: Quantum Computing: Vision and Challenges [arXiv:2403.02240]
-
John Preskill: Beyond NISQ: The Megaquop Machine, talk at Q2B 2024 Silicon Valley (Dec. 2024) [pdf, webpage]
More concerned outlook:
-
DARPA: Quantum Benchmarjing Initiative
“to determine if it’s possible to build an industrially useful quantum computer much faster than conventional predictions. Specifically, QBI is designed to rigorously verify and validate if any quantum computing approach can achieve utility-scale operation — meaning its computational value exceeds its cost — by the year 2033.”
The accompanying video says at 1:25:
“If it turns out, as a lot of us suspect, that that’s really not possible, and it really won’t do something useful, or there isn’t a path, we need to know that, too.”
Quantum programming via monads
Discussion of aspects of quantum programming in terms of monads in functional programming are in
-
Thorsten Altenkirch, Alexander Green, The quantum IO monad, in Semantic Techniques in Quantum Computation, January 2009, appeared in 2010 (pdf, talk slides)
-
J. K. Vizzotto, Thorsten Altenkirch, A. Sabry, Structuring quantum effects: superoperators as arrows (arXiv:quant-ph/0501151)
As linear logic
Discussion of quantum computation as the internal linear logic/linear type theory of compact closed categories is in
-
Samson Abramsky, Ross Duncan, A Categorical Quantum Logic, Mathematical Structures in Computer Science, 2006 (arXiv:quant-ph/0512114)
-
Ross Duncan, Types for quantum mechanics, 2006 (pdf, slides)
-
Ugo Dal Lago, Claudia Faggian, On Multiplicative Linear Logic, Modality and Quantum Circuits, EPTCS 95, 2012, pp. 55-66 (arXiv:1210.0613)
An exposition along these lines is in
- John Baez, Mike Stay, Physics, topology, logic and computation: a rosetta stone, arxiv/0903.0340; in “New Structures for Physics”, ed. Bob Coecke, Lecture Notes in Physics 813, Springer, Berlin, 2011, pp. 95-174
Quantum information theory via String diagrams
General
The observation that a natural language for quantum information theory and quantum computation, specifically for quantum circuit diagrams, is that of string diagrams in †-compact categories (see quantum information theory via dagger-compact categories):
-
Samson Abramsky, Bob Coecke, A categorical semantics of quantum protocols, Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) arXiv:quant-ph/0402130, doi:10.1109/LICS.2004.1319636
-
Samson Abramsky, Bob Coecke, Abstract Physical Traces, Theory and Applications of Categories, 14 6 (2005) 111-124. [tac:14-06, arXiv:0910.3144]
-
Samson Abramsky, Bob Coecke, Categorical quantum mechanics, in Handbook of Quantum Logic and Quantum Structures, Elsevier (2008) arXiv:0808.1023, ISBN:9780080931661, doi:10.1109/LICS.2004.1319636
-
Bob Coecke, De-linearizing Linearity: Projective Quantum Axiomatics from Strong Compact Closure, Proceedings of the 3rd International Workshop on Quantum Programming Languages (2005), Electronic Notes in Theoretical Computer Science 170 (2007) 49-72 [doi:10.1016/j.entcs.2006.12.011, arXiv:quant-ph/0506134]
On the relation to quantum logic/linear logic:
-
Samson Abramsky, Ross Duncan, A Categorical Quantum Logic, Mathematical Structures in Computer Science 16 3 (2006) arXiv:quant-ph/0512114, doi:10.1017/S0960129506005275
-
Ross Duncan, Types for quantum mechanics, 2006 pdf, slides
Early exposition with introduction to monoidal category theory:
-
Bob Coecke, Kindergarten quantum mechanics arXiv:quant-ph/0510032
-
Bob Coecke, Introducing categories to the practicing physicist arXiv:0808.1032
-
John Baez, Mike Stay, Physics, topology, logic and computation: a rosetta stone in: New Structures for Physics, Bob Coecke (ed.), Lecture Notes in Physics 813, Springer (2011) 95-174 arxiv/0903.0340
-
Bob Coecke, Eric Oliver Paquette, Categories for the practising physicist, in: New Structures for Physics, Lecture Notes in Physics 813, Springer (2010) arXiv:0905.3010, doi:10.1007/978-3-642-12821-9_3
-
Bob Coecke, Quantum Picturalism, Contemporary Physics 51 1 (2010) arXiv:0908.1787, doi:10.1080/00107510903257624
Review in contrast to quantum logic:
- Samson Abramsky, Bob Coecke, Physics from Computer Science: a Position Statement, International Journal of Unconventional Computing 3 3 (2007) pdf, ijuc-3-3-p-179-197
and with emphasis on quantum computation:
- Jamie Vicary, The Topology of Quantum Algorithms, (LICS 2013) Proceedings of 28th Annual ACM/IEEE Symposium on Logic in Computer Science (2013) 93-102 arXiv:1209.3917, doi:10.1109/LICS.2013.14
Generalization to quantum operations on mixed states (completely positive maps of density matrices):
-
Peter Selinger, Dagger compact closed categories and completely positive maps, Electronic Notes in Theoretical Computer Science 170 (2007) 139-163 doi:10.1016/j.entcs.2006.12.018, web, pdf
-
Bob Coecke, Chris Heunen, Pictures of complete positivity in arbitrary dimension, Information and Computation 250 50-58 (2016) arXiv:1110.3055, doi:10.1016/j.ic.2016.02.007
-
Bob Coecke, Chris Heunen, Aleks Kissinger,
Categories of Quantum and Classical Channels, EPTCS 158 (2014) 1-14 arXiv:1408.0049, doi:10.4204/EPTCS.158.1
Textbook accounts (with background on relevant monoidal category theory):
-
Bob Coecke, Aleks Kissinger, Picturing Quantum Processes – A First Course in Quantum Theory and Diagrammatic Reasoning, Cambridge University Press (2017) ISBN:9781107104228
-
Chris Heunen, Jamie Vicary: Categories for Quantum Theory, Oxford University Press (2019) [ISBN:9780198739616]
based on:
Chris Heunen, Jamie Vicary, Lectures on categorical quantum mechanics (2012) [pdf, pdf]
-
Bob Coecke, Stefano Gogioso, Quantum in Pictures, Quantinuum Publications (2023) ISBN 978-1739214715, Quantinuum blog
(focus on ZX-calculus)
Measurement & Classical structures
Formalization of quantum measurement via Frobenius algebra-structures (“classical structures”):
-
Bob Coecke, Duško Pavlović, Quantum measurements without sums, in Louis Kauffman, Samuel Lomonaco (eds.), Mathematics of Quantum Computation and Quantum Technology, Taylor & Francis (2008) 559-596 arXiv:quant-ph/0608035, doi:10.1201/9781584889007
-
Bob Coecke, Eric Oliver Paquette, POVMs and Naimark’s theorem without sums, Electronic Notes in Theoretical Computer Science 210 (2008) 15-31 arXiv:quant-ph/0608072, doi:10.1016/j.entcs.2008.04.015
-
Bob Coecke, Eric Oliver Paquette, Duško Pavlović, Classical and quantum structuralism, in: Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 29-69 arXiv:0904.1997, doi:10.1017/CBO9781139193313.003
-
Bob Coecke, Duško Pavlović, Jamie Vicary, A new description of orthogonal bases, Mathematical Structures in Computer Science 23 3 (2012) 555- 567 arXiv:0810.0812, doi:10.1017/S0960129512000047
and the evolution of the “classical structures”-monad into the “spider”-diagrams (terminology for special Frobenius normal form, originating in Coecke & Paquette 2008, p. 6, Coecke & Duncan 2008, Thm. 1) of the ZX-calculus:
-
Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) doi:10.1007/978-3-540-70583-3_25
-
Aleks Kissinger, §§2 in: Graph Rewrite Systems for Classical Structures in -Symmetric Monoidal Categories, MSc thesis, Oxford (2008) pdf, pdf
-
Aleks Kissinger, §4 in: Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 doi:10.1007/978-3-642-02614-0_12
-
Bob Coecke, Ross Duncan, Def. 6.4 in: Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 arXiv:0906.4725, doi:10.1088/1367-2630/13/4/043016
ZX-Calculus
Evolution of the “classical structures”-Frobenius algebra (above) into the “spider”-ingredient of the ZX-calculus for specific control of quantum circuit-diagrams:
-
Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) doi:10.1007/978-3-540-70583-3_25
-
Aleks Kissinger, Graph Rewrite Systems for Classical Structures in -Symmetric Monoidal Categories, MSc thesis, Oxford (2008) pdf, pdf
-
Aleks Kissinger, Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 doi:10.1007/978-3-642-02614-0_12
-
Bob Coecke, Ross Duncan, Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 arXiv:0906.4725, doi:10.1088/1367-2630/13/4/043016
Relating the ZX-calculus to braided fusion categories for anyon braiding:
- Fatimah Rita Ahmadi, Aleks Kissinger, Topological Quantum Computation Through the Lens of Categorical Quantum Mechanics arXiv:2211.03855
Topological quantum computing
topological quantum computation is discussed in
-
Michael Freedman, Alexei Kitaev, Michael J. Larsen, Zhenghan Wang, Topological Quantum Computation (arXiv:quant-ph/0101025)
-
Zhenghan Wang, Topologization of electron liquids with Chern-Simons theory and quantum computation (arXiv:cond-mat/0601285)
-
Michael Freedman, Michael Larsen, Zhenghan Wang, A modular functor which is universal for quantum computation, Communications in Mathematical Physics 227 (2002) 605–622 [arXiv:quant-ph/0001108, doi:10.1007/s002200200645]
-
Alexei Kitaev, Fault-tolerant quantum computation by anyons, Annals Phys. 303 (2003) 2-30 (arXiv:quant-ph/9707021)
Relation to tensor networks
Relation to tensor networks, specifically matrix product states:
- Yiqing Zhou, E. Miles Stoudenmire, Xavier Waintal, What limits the simulation of quantum computers?, arXiv:2002.07730
Spin resonance qbits
The idea of spin resonance qbits, i.e. of qbits realized on quantum mechanical spinors (e.g. electron-spin or nucleus-spin) and manipulated via spin resonance:
- Daniel Loss, David P. DiVincenzo, Quantum Computation with Quantum Dots, Phys. Rev. A 57 120 (1998) arXiv:cond-mat/9701055, doi:10.1103/PhysRevA.57.120
The very first proof-of-principle quantum computations were made with nuclear magnetic resonance-technology:
-
D. G. Cory et al, NMR Based Quantum Information Processing: Achievements and Prospects, Fortsch. Phys. 48 9-11 (2000) 875-907 arXiv:quant-ph/0004104
-
Jonathan A. Jones, Quantum Computing and Nuclear Magnetic Resonance, PhysChemComm 11 (2001) doi:10.1039/b103231n, arXiv:quant-ph/0106067
-
Jonathan A. Jones, Quantum Computing with NMR, Prog. NMR Spectrosc. 59 (2011) 91-120 doi:10.1016/j.pnmrs.2010.11.001, arXiv:1011.1382
-
Dorothea Golze, Maik Icker, Stefan Berger, Implementation of two-qubit and three-qubit quantum computers using liquid-state nuclear magnetic resonance, Concepts in Magnetic Resonance 40A 1 (2012) 25-37 doi:10.1002/cmr.a.21222
-
NMR Quantum Computing (2012) slides pdf
-
Tao Xin et al., Nuclear magnetic resonance for quantum computing: Techniques and recent achievements (Topic Review - Solid-state quantum information processing), Chinese Physics B 27 020308 doi:10.1088/1674-1056/27/2/020308
See also:
- Lieven Vandersypen, Mark Eriksson: Quantum computing with semiconductor spins, Physics Today 72 8 (2019) 38 [doi:10.1063/PT.3.4270]
Monograph:
- Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy, section 10 of: Quantum Computing Devices – Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]
Exposition, review and outlook:
-
Raymond Laflamme, Emanuel Knill, et al., Introduction to NMR Quantum Information Processing, Proceedings of the International School of Physics “Enrico Fermi” 148 Experimental Quantum Computation and Information [arXiv:quant-ph/0207172]
-
Asif Equbal, Molecular spin qubits for future quantum technology, talk at CQTS (Nov 2022) [slides: pdf, video: rec]
-
Jonathan A. Jones, Controlling NMR spin systems for quantum computation, Spectroscopy 140–141 (2024) 49-85 [doi:10.1016/j.pnmrs.2024.02.002, arXiv:2402.01308]
“Nuclear magnetic resonance is arguably both the best available quantum technology for implementing simple quantum computing experiments and the worst technology for building large scale quantum computers that has ever been seriously put forward. After a few years of rapid growth, leading to an implementation of Shor’s quantum factoring algorithm in a seven-spin system, the field started to reach its natural limits and further progress became challenging. […] the user friendliness of NMR implementations means that they remain popular for proof-of-principle demonstrations of simple quantum information protocols.”
See also:
-
Wikipedia, Spin qbit quantum computer
-
Wikipedia, Nuclear magnetic resonance quantum computer
More on implementation of quantum logic gates on qbits realized on nucleon-spin, via pulse protocols in NMR-technology:
- Price, Somaroo, Tseng, Gore, Fahmy,, Havel, Cory: Construction and Implementation of NMR Quantum Logic Gates for Two Spin Systems, Journal of Magnetic Resonance 140 2 (1999) 371-378 doi;10.1006/jmre.1999.1851
and analogously on electron-spin:
- M. Yu. Volkov and K. M. Salikhov, Pulse Protocols for Quantum Computing with Electron Spins as Qubits, Appl Magn Reson 41 (2011) 145–154 doi:10.1007/s00723-011-0297-2
For references on spin resonance qbits realized on a nitrogen-vacancy center in diamond, see there.
There exist toy desktop quantum computers for educational purposes, operating on a couple of nuclear magnetic resonance qbits at room temperature :
-
SpinQ: SpinQ Triangulum: a commercial three-qubit desktop quantum computer arXiv:2202.02983
Superconducting qbits
On realizing qbits and quantum gates (hence quantum computation) via quantum states of magnetic flux through (Josephson junctions in) superconductors, manipulated via electromagnetic pulses:
-
Michel H. Devoret, A. Wallraff, J. M. Martinis, Superconducting Qubits: A Short Review [arXiv:cond-mat/0411174]
-
John Clarke, Frank K. Wilhelm, Superconducting quantum bits, Nature 453 (2008) 1031–1042 doi:10.1038/nature07128
-
Jerry Moy Chow, Quantum Information Processing with Superconducting Qubits (2010) pdf
-
Michel H. Devoret, R. J. Schoelkopf, Superconducting Circuits for Quantum Information: An Outlook, Science 339 6124 (2013) 1169-1174 [doi:10.1126/science.1231930]
-
Jay M. Gambetta, Jerry M. Chow, Matthias Steffen, Building logical qubits in a superconducting quantum computing system, npj Quantum Information 3 2 (2017) doi:10.1038/s41534-016-0004-0
-
Morten Kjaergaard et al. Superconducting Qubits: Current State of Play, Annual Review of Condensed Matter Physics 11 (2019) 369-395 doi:10.1146/annurev-conmatphys-031119-050605
-
He-Liang Huang, Dachao Wu, Daojin Fan, Xiaobo Zhu, Superconducting Quantum Computing: A Review, Science China Information Sciences 63 8 (2020) 1-32 arXiv:2006.10433, doi:10.1007/s11432-020-2881-9
-
S. Kwon et al., Gate-based superconducting quantum computing, Journal of Applied Physics 129 (2021) 041102 doi:10.1063/5.0029735
-
Olivier Ezratty, Perspective on superconducting qubit quantum computing, Eur. Phys. J. A 59 94 (2023) [doi:10.1140/epja/s10050-023-01006-7]
Monograph:
- Chen, Church, Englert, Henkel, Rohwedder, Scully, Zubairy, section 9 of: Quantum Computing Devices Principles, Designs, and Analysis, Routledge (2007) [ISBN:9780367390372]
Fine detail of the pulse control:
-
M. Werninghaus, D. J. Egger, F. Roy, S. Machnes, F. K. Wilhelm, S. Filipp: Leakage reduction in fast superconducting qubit gates via optimal control, npj Quantum Information 7 14 (2021) doi:10.1038/s41534-020-00346-2
-
M. Carroll, S. Rosenblatt, P. Jurcevic, I. Lauer & A. Kandala. Dynamics of superconducting qubit relaxation times, npj Quantum Information 8 132 (2022) doi:10.1038/s41534-022-00643-y
-
Elisha Siddiqui Matekole, Yao-Lung L. Fang, Meifeng Lin, Methods and Results for Quantum Optimal Pulse Control on Superconducting Qubit Systems, 2022 IEEE International Parallel and Distributed Processing Symposium Workshops (2022) arXiv:2202.03260, doi:10.1109/IPDPSW55747.2022.00102
Corrections due to quasiparticle-excitations:
- Leonid I. Glazman, Gianluigi Catelani, Bogoliubov Quasiparticles in Superconducting Qubits, SciPost Phys. Lect. Notes 31 (2021) [arXiv:2003.04366, doi:10.21468/SciPostPhysLectNotes.31]
Photonic qbits
Realization in photonics:
- Han-Shen Zhong et al. Quantum computational advantage using photons, Science 370, n. 6523 (2020) 1460-1463 doi
Commercial quantum computers
Since 2019, NISQ quantum computers can be accessed through cloud services:
-
New Scientist, IBM unveils its first commercial quantum computer (Jan 2019)
-
IBM Quantum (Cloud service)
There exist toy desktop quantum computers for educational purposes, operating on a couple of nuclear magnetic resonance qbits at room temperature :
-
SpinQ: SpinQ Triangulum: a commercial three-qubit desktop quantum computer [arXiv:2202.02983]
Last revised on August 21, 2025 at 10:27:48. See the history of this page for a list of all contributions to it.
