nLab quantum state preparation

Idea

In quantum physics and especially in quantum information theory, by state preparation one refers to a process (either in actual experiments or theoretically as a kind of quantum gate-operation) which, possibly conditioned on a classical parameter $b$, “produces” a predefined quantum state $\vert b \rangle \,\in\, \mathscr{H}$ in a given space of quantum states $\mathscr{H}$.

For example, for a qbit data type there are, by definition of qbits, two canonical basis states $\vert 0 \rangle, \vert 1 \rangle \,\in\, \mathbb{C}^2$ to be prepared, depending on a classical parameter which may be understood as of boolean type (where we set $Bool \,\coloneqq\, \{0, 1\}$).

The various fundamental quantum physics phenomena at play here may be identified with four modal-units of quantum modal logic (as discussed at quantum circuits via dependent linear types):

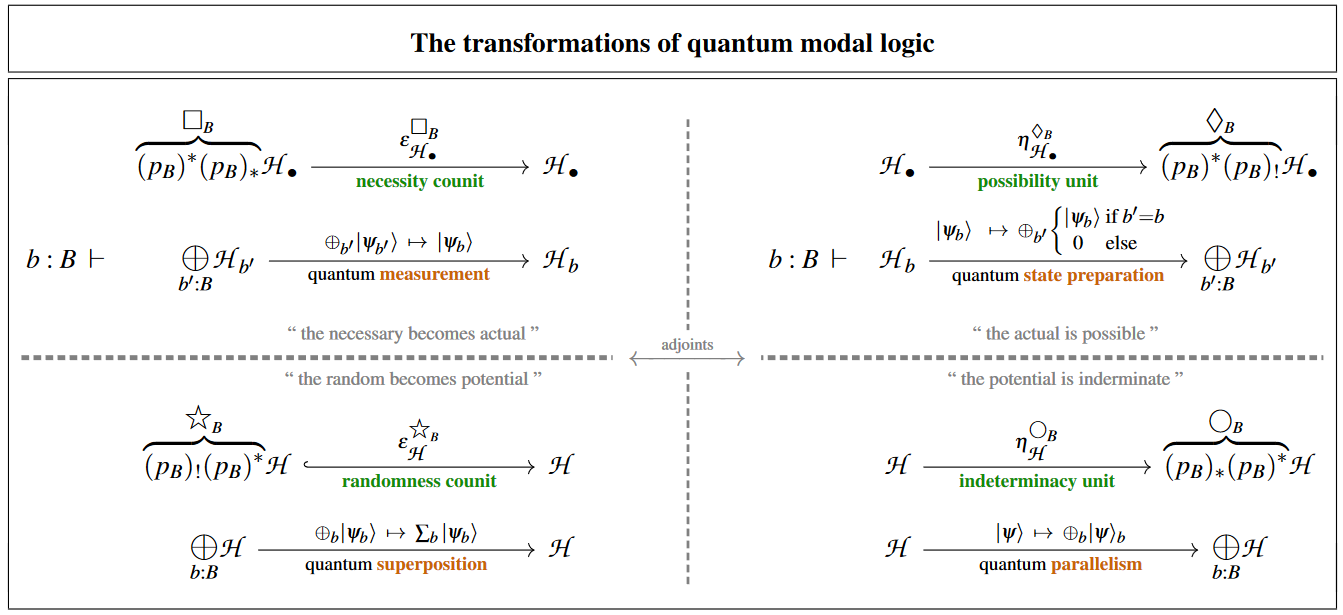
quantum measurement	quantum state preparation
quantum superposition	quantum parallelism

Explicitly, in the language¹ of modal quantum logic on dependent linear types (see at quantum circuits via dependent linear types), the conditional preparation of a qbit-state reads as follows:

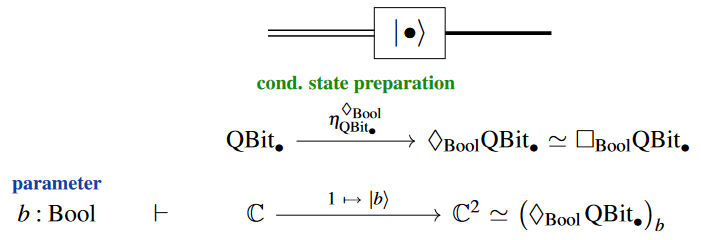
and the unconditional state preparation is of this form:

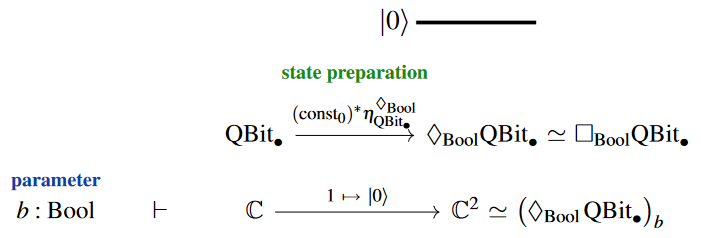
Other states may be prepared by first preparing a qbit-state and then sending it through some quantum gate.

For instance, the Bell state on two qbits may be prepared by first preparing a tensor product of two $\vert 0 \rangle$-states and then sending one through a Hadamard gate and then the resulting two qbits through a CNOT gate:

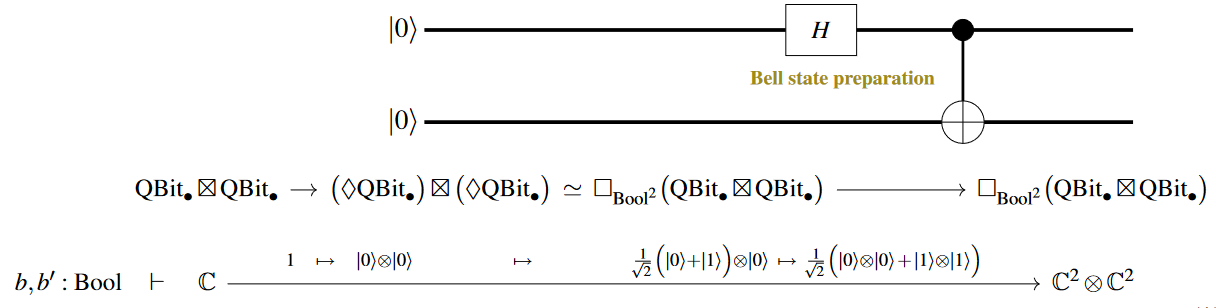
This is used in many common quantum circuits, such as for instance in the quantum teleportation-protocol.

References

Standard textbook accounts:

• Michael A. Nielsen, Isaac L. Chuang, §7.2 in: Quantum computation and quantum information, Cambridge University Press (2000) [doi:10.1017/CBO9780511976667, pdf, pdf]

---

1. The above text follows Quantum Certification via Linear Homotopy Types. ↩