nLab supersymmetry breaking
Context
Algebraic Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Contents
Idea
The spontaneous breaking of supersymmetry. Key to all phenomenology with global low energy supersymmetry. In supergravity for instance due to gravitino condensation or gaugino condensation.
In a supersymmetric Lagrangian field theory, the stress-energy tensor is the image of the supersymmetry Noether's conserved current under the super Lie bracket with the supercharge
and hence the vacuum expectation value of the stress-energy tensor is
which hence vanishes if the vacuum state is supersymmetric, hence if supersymmetry is not spontaneously broken.
Conversely, this means that supersymmetry, as opposed to (gauge) symmetries of the Lagrangian not related to gravity, is broken by a positive vacuum energy
(e.g Witten 81, (3), (4))
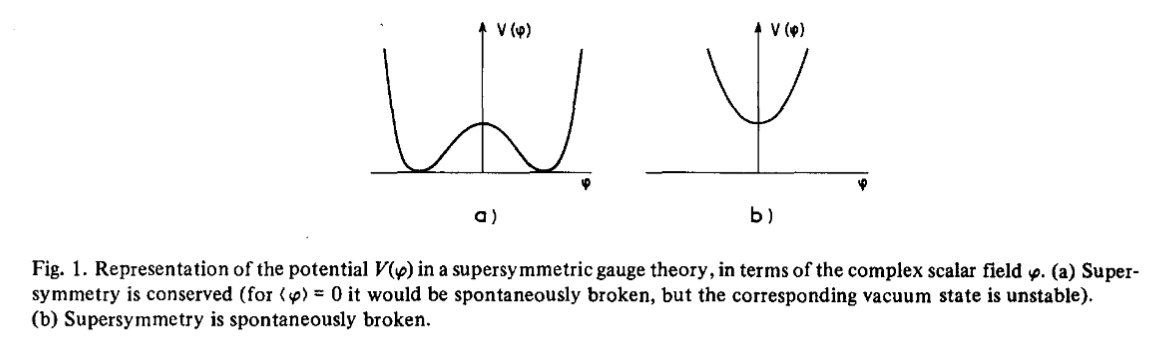
graphics grabbed from Fayet-Ferrara 77, Fig. 1 on p. 286 (38 of 86)
Examples
Scherk-Schwarz mechanism
The Scherk-Schwarz mechanism (Scherk-Schwarz 79) is the spontaneous supersymmetry breaking by KK-compactification on a circle whose spin structure imposes anti-periodic boundary conditions for fermion fields.
Related concepts
References
Original articles include
-
Pierre Fayet, Sergio Ferrara, Supersymmetry, Physics Reports Volume 32, Issue 5, September 1977, Pages 249-334 (doi:10.1016/0370-1573(77)90066-7)
-
Edward Witten, Dynamical breaking of supersymmetry, Nuclear Physics B Volume 188, Issue 3, 5 October 1981, Pages 513-554 (doi:10.1016/0550-3213(81)90006-7)
Review includes
-
Hans-Peter Nilles, Supersymmetry, supergravity and particle physics, Physics Reports Volume 110, Issues 1–2, August 1984, Pages 1-162 (doi:10.1016/0370-1573(84)90008-5)
-
Hans-Peter Nilles, Hidden Sector Supergravity Breakdown, Nucl. Phys. Proc. Suppl. 101 (2001) 237-250 (arXiv:hep-ph/0106063)
-
Yael Shadmi, Yuri Shirman. Dynamical supersymmetry breaking. Reviews of Modern Physics 72, no. 1 (2000): 25. (doi) (arXiv:hep-th/9907225)
-
Yael Shadmi, Supersymmetry breaking (arXiv:hep-th/0601076)
-
Matteo Bertolini, Supersymmetry breaking (pdf)
A quantitative analysis showing that locally supersymmetric spacetime theories will generically not exhibit global spacetime supersymmetry is
- Keith Dienes, Michael Lennek, David Sénéchal, Vaibhav Wasnik, Is SUSY Natural? NewJ.Phys.10:085003,2008 (arXiv:0804.4718)
Discussion of supersymmetry breaking unified with cosmic inflation via higher curvature corrections of supergravity – in the Starobinsky model of cosmic inflation – includes
-
Sergio Ferrara, Alex Kehagias, Higher Curvature Supergravity, Supersymmetry Breaking and Inflation (arXiv:1407.5187)
-
I. Dalianis, F. Farakos, A. Kehagias, A. Riotto, R. von Unge, Supersymmetry Breaking and Inflation from Higher Curvature Supergravity (arXiv:1409.8299)
Last revised on June 7, 2024 at 19:13:54. See the history of this page for a list of all contributions to it.