nLab
gauged supergravity

Idea

Theories of supergravity always contain a global symmetry called R-symmetry. In some cases this is promoted to a local symmetry, such that there is a gauge field (connection on a bundle) with coefficients in that group. These are called gauged supergravity theories.

Properties

From dimensional reduction

For many cases gauged supergravity theories are obtained by dimensional reduction from 11-dimensional supergravity or type II supergravity, which themselves do not contain a gauge field. This appears in the reduction by the Kaluza-Klein mechanism.

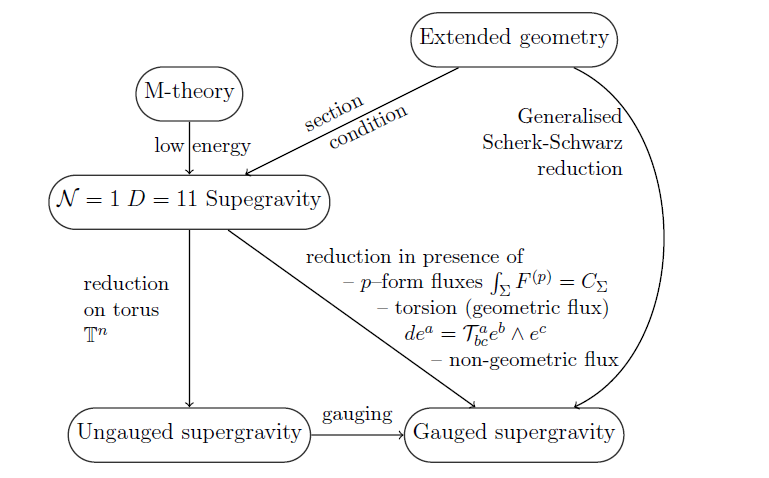
Examples

Some examples are discussed at 7-dimensional supergravity.

References

• Henning Samtleben, Lectures on Gauged Supergravity and Flux Compactifications (arXiv:0808.4076)