nLab adinkra

Idea

In super-representation theory, what is called adinkras (Faux-Gates 04) is a graphical tool for denoting those representations (super multiplets) of the $\mathcal{N}$-extended supersymmetry algebras in one dimension (supersymmetric quantum mechanics with N supersymmetries) for which the supersymmetry generators act, up to derivatives and prefactors, by permutation of superfield components. These are called adinkraic representations (Zhang 13, p. 16).

While adinkraic representations are special among all representations of the 1-dimensional $\mathcal{N}$-extended supersymmetry algebra, the idea is that the dimensional reduction of representations (supermultiplets) of higher dimensional supersymmetry algebras down to 1d are of this form, at least for dimensional reduction from $d = 4$ and $N = \mathbf{4}$ (GGMPPRW 09, section 3, Gates-Hubsch-Stiffler 14).

The classification of adinkras, and hence of adinkraic representations, turns out to be controlled by linear codes (Doran & Faux & Gates & HubschIgaLandweberMiller 11) and to be related to certain special super Riemann surfaces via dessins d'enfants (Doran & Iga & Landweber & Mendez-Diez 13, Doran & Iga & Kostiuk &Mendes-Diez 16).

Definition

For background, see at geometry of physics – supersymmetry.

For $N \in \mathbb{N}$, write $\mathbb{R}^{1 \vert N}$ for the super Lie algebra over the real numbers that is spanned by a single generator $P$ in even (i.e., bosonic) degree and $N$ generators $Q_I$, $I \in \{1, 2, \cdots, N\}$ in odd (i.e., fermionic) degree, whose only non-trivial components of the super-Lie bracket are

$$[Q_I, Q_J] = 2 \delta_{I J} P = \left\{ \array{ 2 P & \vert & I = J \\ 0 & \vert & \text{otherwise} } \right.$$

This is the 1-dimensional $N$-extended super translation super Lie algebra. We may think of this as the super-translational symmetry of 1-dimensional $N$-extended super Minkowski spacetime.

Consider then super Lie algebra representations of $\mathbb{R}^{1 \vert N}$ on super vector spaces of smooth superfields on $\mathbb{R}^{1 \vert N}$ (regarded as a supermanifold) and such that the bosonic generator $P$ acts as the derivative operator on smooth functions on $\mathbb{R}^1$ in each component. If in addition the representation is such that in the canonical linear basis the odd generators $Q_I$ send even/odd basis elements $\phi_i$ to single odd/even basis elements $\psi_j$ (as opposed to linear combinations of them), hence if the $Q_I$ act apart from degree-shift and possibly differentiation by permutations on the components of the superfields, then this representation of $\mathbb{R}^{1\vert N}$ is called adinkraic. (Zhang 13, p. 16).

The corresponding adinkra is the bipartite graph which expresses these permutations:

table grabbed from Doran & Iga & Landweber & Mendez-Diez 13, p. 7

graphics grabbed from Iga-Zhang 15, p. 3

Classification

The topology of an adinkra graph together with its edge coloring in $\{1,2, \cdots, N\}$ is called its chromotopology.

The set of adinkra chromotopologies is equivalent to the set of colored $N$-cubs modulo doubly even length-$N$ linear codes (Doran-Faux-Gates-Hubsch-Iga-Landweber-Miller 11)

(A linear code of length $N$ is a linear subspace of $(\mathbb{F}_2)^N$ for $\mathbb{F}_2$ the prime field with two elements and it is doubly even if every element has weight a multiple of 4. )

see Zhang 13, chapter 2

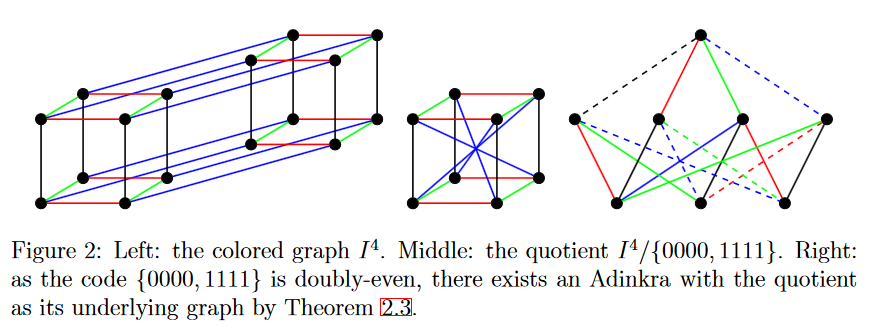
graphics grabbed from Iga-Zhang 15, p. 4

From supermultiplets in higher dimensions

The dimensional reduction of the smallest supermultiplets of $d = 4, N = \mathbf{4}$ supersymmetry down to 1d yield adinkraic representations (GGMPPRW 09, section 3, Gates-Hubsch-Stiffler 14).

Corresponding adinkras for the chiral scalar supermultiplet (CM), the vector multiplet (VM) and the tensor multiplet (TM) look as follows:

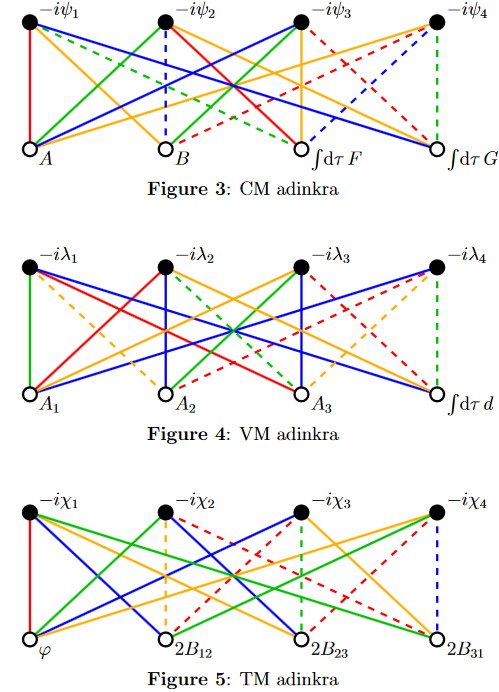
References

For an introduction to adinkras, see the talk

• Lutian Zhao, What is an Adinkra? (2014) [slides pdf]

The concept of adinkras was introduced into supersymmetry representation theory in:

• Michael Faux, Jim Gates, Adinkras: A Graphical Technology for Supersymmetric Representation Theory, Phys. Rev. D 71 (2005) 065002 [hep-th/0408004, doi:10.1103/PhysRevD.71.065002]

and further developed in the article

• Charles Doran, Michael Faux, Jim Gates, Tristan Hübsch, Kevin Iga, Greg Landweber, On Graph-Theoretic Identifications of Adinkras, Supersymmetry Representations and Superfields, Int. J. Mod. Phys. A 22 , (2007) 869-930 [arXiv:math-ph/0512016, doi:10.1142/S0217751X07035112]

and many more (“DFGHIL collaboration”). For instance the relation to Clifford supermodules is discussed in

• Charles Doran, Michael Faux, Jim Gates, Tristan Hübsch, Kevin Iga, Greg Landweber, Off-shell supersymmetry and filtered Clifford supermodules, Algebr Represent Theor 21 (2018) 375–397 &lbraclarXiv:math-ph/0603012, doi:10.1007/s10468-017-9718-8]

kinetic terms are discussed in

• Charles Doran, Michael Faux, Jim Gates, Tristan Hübsch, Kevin Iga, Greg Landweber, Adinkras and the Dynamics of Superspace Prepotentials [arXiv:hep-th/0605269, InSpire:717895]

The classification of adinkras in terms of graphs and linear codes is due to

• Charles Doran, Michael Faux, Jim Gates, Tristan Hübsch, Kevin Iga, Greg Landweber, R. L. Miller, Codes and Supersymmetry in One Dimension, Adv. Theor. Math. Phys. 15 (2011) 1909-1970 [arXiv:1108.4124, doi;10.4310/ATMP.2011.v15.n6.a7]

and discussed in mathematical detail in

• Yan X Zhang, Adinkras for Mathematicians (arXiv:1111.6055)

• Yan X Zhang, The combinatorics of Adinkras, PhD thesis, MIT (2013) (pdf)

The dimensional reduction of the standard supermultiplets of $D = 4, \mathcal{N} = 1$ supersymmetry to adinkraic representations of $D = 1, \mathcal{N}=4$ is due to

• Jim Gates, J. Gonzales, B. MacGregor, J. Parker, R. Polo-Sherk, V. G. J. Rodgers, L. Wassink, $4D$, $\mathcal{N} = 1$ Supersymmetry Genomics (I), JHEP 0912:008 (2009) [arXiv:0902.3830, doi:10.1088/1126-6708/2009/12/008]

• Jim Gates, Tristan Hübsch, Kory Stiffler, Adinkras and SUSY Holography, Int. J. Mod. Phys. A 29 7 (2014) 1450041 [arXiv:1208.5999, doi;10.1142/S0217751X14500419]

See also

• Kevin Iga, Yan Zhang, Structural Theory of 2-d Adinkras (arXiv:1508.00491)

Discussion for $D=11$, $\mathcal{N}=1$:

• Jim Gates, Yangrui Hu, S.-N. Hazel Mak, Adinkra Foundation of Component Decomposition and the Scan for Superconformal Multiplets in 11D, $\mathcal{N} = 1$ Superspace [arXiv:2002.08502, doi:10.1007/JHEP09(2020)089]

The relation of adinkras to special super Riemann surfaces via dessins d'enfants:

• Charles Doran, Kevin Iga, Greg Landweber, Stefan Méndez-Diez, Geometrization of $\mathcal{N}$-Extended 1-Dimensional Supersymmetry Algebras, Adv. Theor. Math. Phys. 19 5 (2015) 1043-1113 [arXiv:1311.3736, doi:10.4310/ATMP.2015.v19.n5.a4, pdf]

• Charles Doran, Kevin Iga, Jordan Kostiuk, Stefan Méndez-Diez, Geometrization of $\mathcal{N}$-Extended 1-Dimensional Supersymmetry Algebras II, Adv. Theor. Math> Physics 22 3 (2018) [arXiv:1610.09983]

Further developments:

• Mathew Calkins, D. E. A. Gates, Jim Gates Jr., Kory Stiffler, Adinkras, 0-branes, Holoraumy and the SUSY QFT/QM Correspondence, International Journal of Modern Physics A 30 11 (2015) 1550050 [arXiv:1501.00101, doi:10.1142/S0217751X15500505]

• S. James Gates Jr., Isaiah B. Hilsenrath, Saul Hilsenrath: Modern Tensor-Spinor Symbolic Algebra Algorithms and Computing Non-Closure Geometry & Holoraumy in $11D$, $\mathcal{N} = 1$ Supergravity [arXiv:2212.00614]

• S. James Gates Jr., Yangrui Hu: Adynkra Genomes, Adynkrafields, and the 4D, $\mathcal{N} = 1$ Supergravity Superfield Prepotential [arXiv:2407.09334]

Discussion in the context of spectral triples is in

• Matilde Marcolli, Nick Zolman, Adinkras, Dessins, Origami, and Supersymmetry Spectral Triples (arXiv:1606.04463)

See also

• Wes Caldwell, Alejandro Diaz, Isaac Friend, Jim Gates, Jr., Siddhartha Harmalkar, Tamar Lambert-Brown, Daniel Lay, Karina Martirosova, Victor Meszaros, Mayowa Omokanwaye, Shaina Rudman, Daniel Shin, Anthony Vershov, On the Four Dimensional Holoraumy of the $4D$, $\mathcal{N} = 1$ Complex Linear Supermultiplet (arXiv:1702.05453)

• Kevin Iga, Adinkras: Graphs of Clifford Algebra Representations, Supersymmetry, and Codes (arXiv:2110.01665)

• Wikipedia, Adinkra symbols (physics)

In relation to pure spinors:

• Richard Eager, Simone Noja, Raphael Senghaas, Johannes Walcher, Adinkras and Pure Spinors [arXiv:2404.07167]

Relation to cellular automata?:

• S. James Gates Jr., Youngik (Tom) Lee: A Précis: Minimal Four Color Holoraumy and Wolfram’s “New Kind of Science” Paradigm [arXiv:2408.09342]