nLab group-completed configuration space of points

Group completed configuration spaces of unlabeled points

We briefly review Okuyama’s configuration-spaces of “charged strings” as models for the group completion of plain configuration spaces of points without labels (or rather: with labels in $S^0$), pointing out how the equivalence relations involved have a natural interpretation in terms of open string worldsheets:

• Charged particles and strings

Using this, we observe that based loops in Okuyama’s configuration space of points in the plane $\mathbb{R}^2$ are essentially identified with framed oriented links whose class in the fundamental group $\simeq \pi^3(S^2) \simeq \mathbb{Z}$ is twice their total linking number plus their framing number (thus reproving the Pontrjagin theorem in these dimensions):

• Charged string loops as framed links

Charged particles and strings

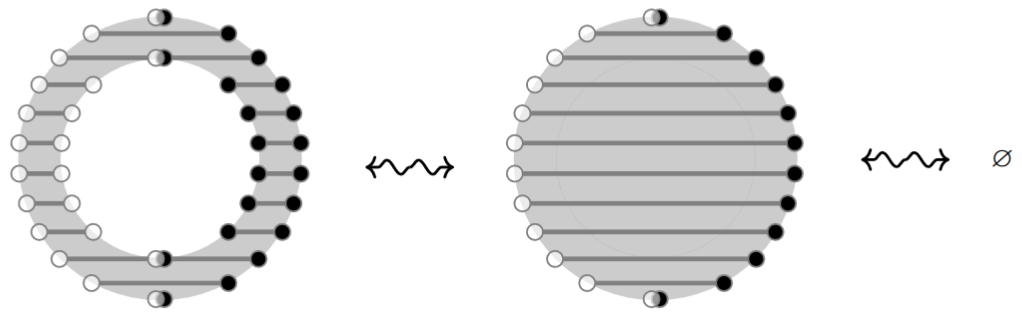
Write $Conf(\mathbb{R}^n)$ for the “plain” configuration space of unlabeled and unordered points in the Cartesian space (Euclidean space) $\mathbb{R}^n$, hence for the evident topological space of finite subsets of $\mathbb{R}^n$.

This space naturally carries the structure of a partial abelian topological monoid, where the addition of a pair of configurations is defined if they are disjoint, in which case it is given by their (necessarily disjoint) union [Segal 1973, p. 215].

Here we write

$$\mathbb{G}Conf(\mathbb{R}^n) \;\coloneqq\; \Omega B_{\sqcup} Conf(\mathbb{R}^n)$$

for the group completion of the configuration space with respect to this partial operation of disjoint union.

Segal 1973, Thm. 1 says, in particular, that this group completed configuration space is weak homotopy equivalent to the $n$-fold iterated loop space of the $n$-sphere $S^n$ (the $n$-Cohomotopy cocycle space of the one-point compactification $\mathbb{R}^n_{cpt}$ of Euclidean space):

(1)$$\mathbb{G} Conf(\mathbb{R}^n) \;\simeq\; \Omega^n S^n \,,$$

This motivates asking for more explicit descriptions of the group completed configuration space of points, itself as a configuration space, now of objects somewhat richer than plain points.

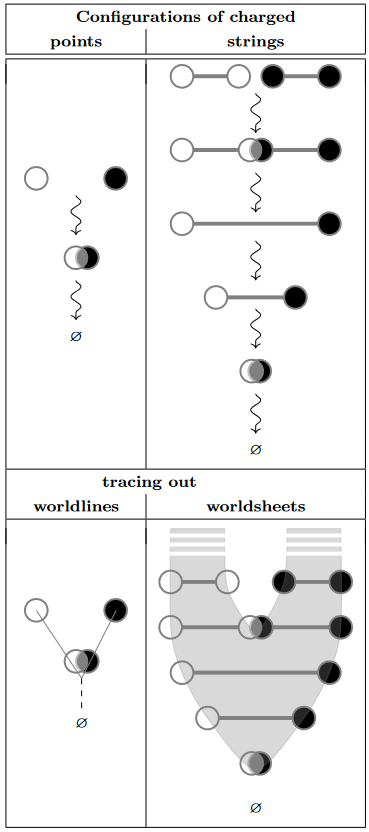
Since the group completion must introduce the existence of a kind of “anti-points” much in the sense of antiparticles, it is tempting to think that $\mathbb{G}Conf(\mathbb{R}^n)$ should be equivalent to the configuration space $Conf^{\pm}(\mathbb{R}^n)$ of charged points, where each point in a configuration carries a label in $\{\pm 1\}$ and where equal-charged points cannot coincide (they “repel”) while pairs of oppositely charged points may coincide in which case they annihilate [McDuff 1975, p. 94]. However, this is not the case: $Conf^{\pm}(\mathbb{R}^n) \neq \mathbb{G}Conf(\mathbb{R}^n)$ [McDuff 1975, p. 96].

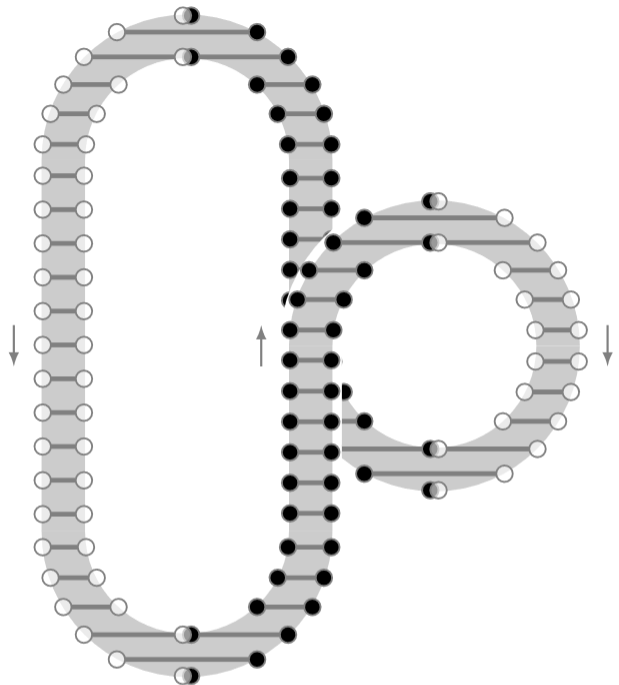
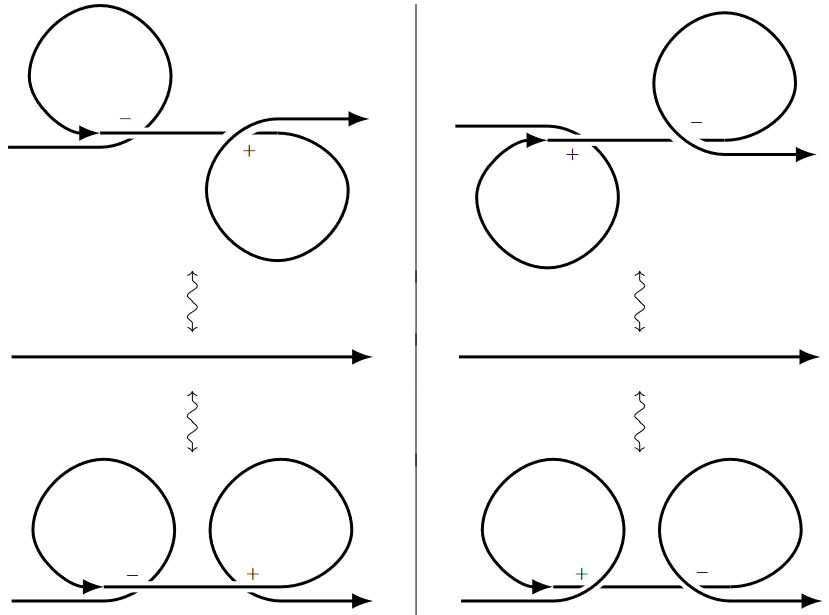
Still, the basic idea can be salvaged [Okuyama 2005] if only one allows charged points to be replaced by “strings” — concretely: straight line segments of finite lenght in $\mathbb{R}^n$ each parallel to, say, the first coordinate axis — with charged endpoints, where pair creation/annihilation of strings smoothens out the corresponding interaction of points, in the familiar way in which interactions in string theory smoothen out singular Feynman diagrams (only that here this is not postulated but emerges in order that the resulting moduli space models $\mathbb{G}Conf(\mathbb{R}^n)$):

On the right, if a filled circle is taken to indicate that the corresponding point is part of the interval, while an open circle indicates that it is not, then the curved arrows correspond to continuous paths in the configuration space of intervals, $Conf^I(\mathbb{R}^n)$, according to Okuyama 2005, Def. 3.1-2 — there denoted $I_n(S^0)_{\mathbb{R}}$.

With this stringy resolution of the charged points, the expected equivalence does hold [Okuyama 2005, Thm. 1]:

(2)$$Conf^I(\mathbb{R}^n) \;\; \simeq \;\; \mathbb{G}Conf(\mathbb{R}^n) \,.$$

Charged string loops as framed links

It follows that the fundamental group of the configuration space of charged strings in the plane $\mathbb{R}^2$ is

(3)$$\begin{array}{ll} \pi_1\big( Conf^I(\mathbb{R}^2) \big) & \simeq\;\; \pi_1\big( \mathbb{G}Conf(\mathbb{R}^2) \big) \;\;\simeq\;\; \pi_1\big( \Omega^2 S^2 \big) \;\;\simeq\;\; \pi_0\big( \Omega(\Omega^2 S^2) \big) \;\;\simeq\;\; \pi_0\big( \Omega^3 S^2) \big) \;\;\simeq\;\; \pi^3(S^2) \\ &\simeq\;\; \mathbb{Z} \,, \end{array}$$

where the first isomorphism is by Okuyama’s theorem (2), the second by Segal’s theorem (1) and the last one is the statement that the 3d homotopy group of the 2-sphere is the free group generated by the Hopf fibration.

Hence we ask which loop diagram of charged strings corresponds to the Hopf fibration, under this sequences of isomorphisms.

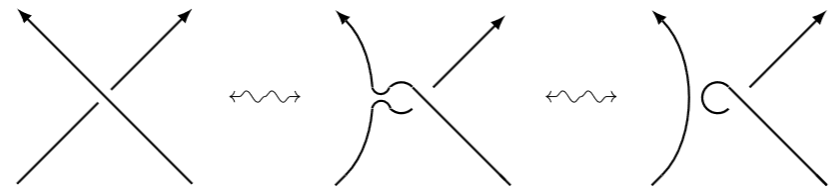
In the following analysis we consider continuous paths of continuous paths of configurations of charged strings – hence continuous maps $[0,1]^2 \to Conf^I(\mathbb{R}^2)$, the two main building blocks being the oriented saddle

and the appearance/vanishing of the plain loop diagram.

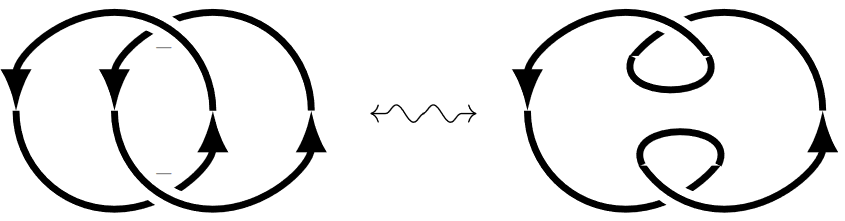
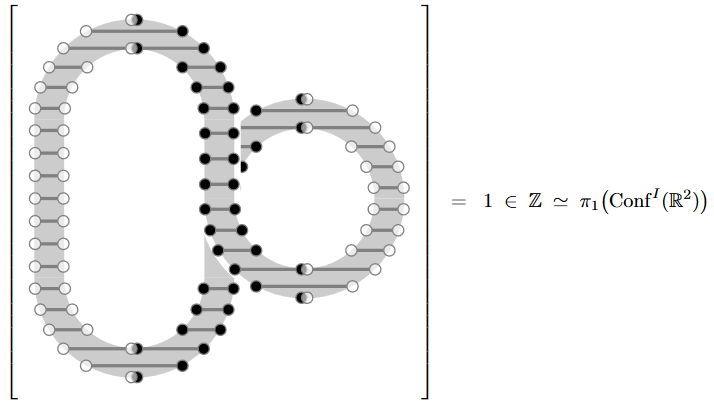
The following based loop should have a non-trivial class in $\pi_1\big(Conf^I(\mathbb{R}^2)\big)$ and we will argue (Thm. below) that all other based loops have classes which are integral multiples of this one:

This example brings out the key difference between loops in McDuff’s configuration space of charged points and loops in Okuyama’s configuration spaces of charged strings: The former may essentially be regarded as oriented links, while the latter carry the further structure of framed links.

As such, the above is the unknot-link but equipped with non-vanishing framing number $+1$ (say, the choice of the sign is a convention).

Its composition with itself, as an element of the fundamental group, yields the framed knot sum which is the unknot with framing number $+2$:

(4)

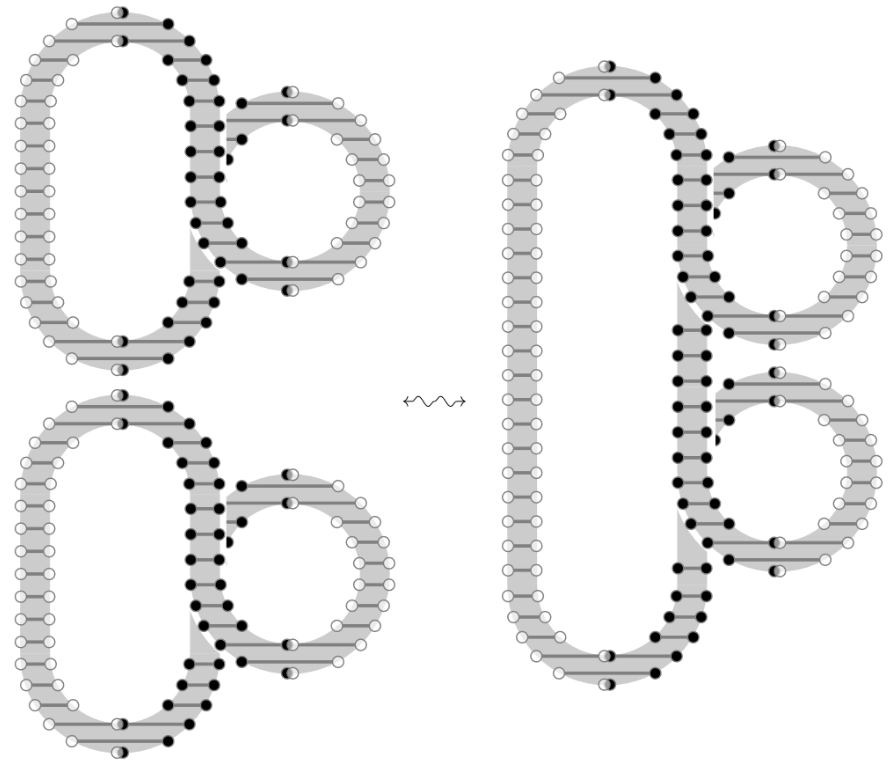
In view of this, we find that the charged stringy version of the Hopf link is equivalent, as an element of $\pi_1\big(Conf^I(\mathbb{R}^2)\big)$ and via the above saddle move, to the unknot equipped with framing number $+2$:

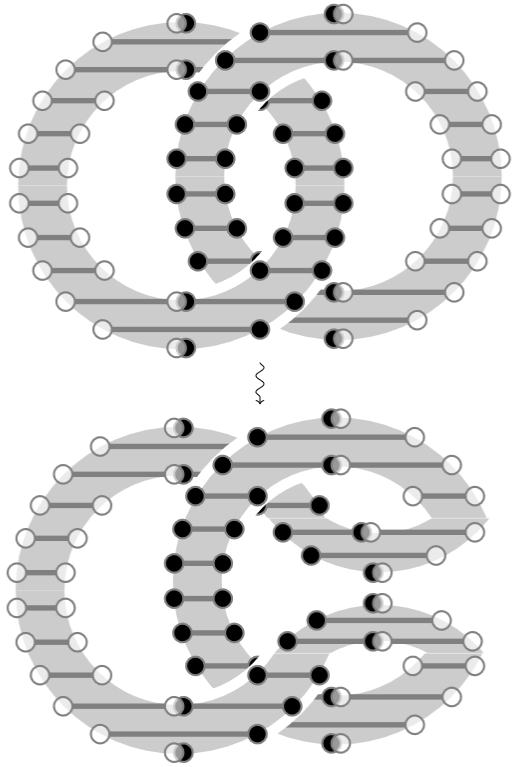
In fact, by applying the same saddle move on the left, this shows that the Hopf link represents twice the class of the previous example in $\pi_1\big(Conf^I(\mathbb{R}^2)\big)$.

Analogously, the Hopf link with the opposite relative orientation represents $-2$ times that unit class:

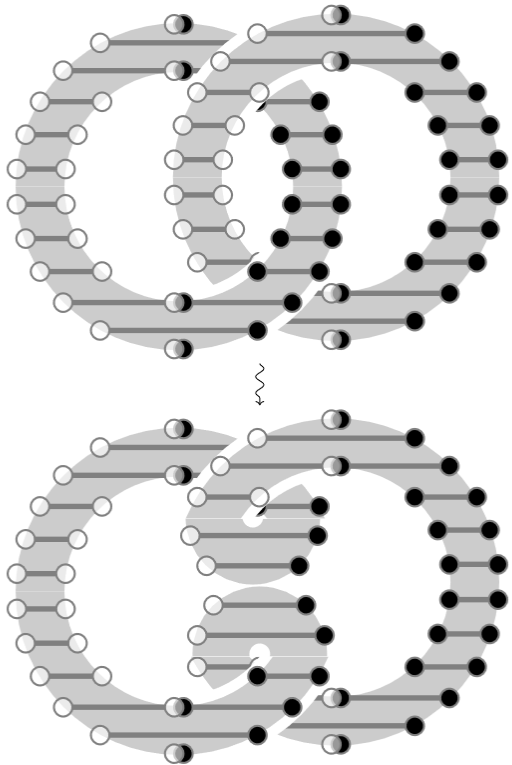
These examples should suffice to illustrate how framed oriented link diagrams may be regarded as based loops in the Okuyama configuration space, and conversely how every based loop of Okuyama configurations – possibly up to some slight continuous deformation – comes from a framed oriented link diagram in this way. Therefore, from now on we just draw framed oriented link diagrams, in fact we will draw just oriented link diagrams and declare the framing to be the blackboard framing (as implicit already in the above examples).

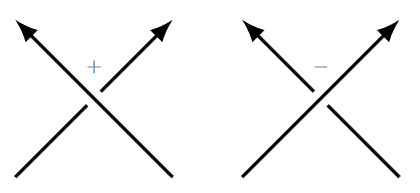
Our sign convention for crossing numbers shall be

In this link-diagram notation, the above stringy saddle- and vacuum-move look as shown on the left here:

(5)

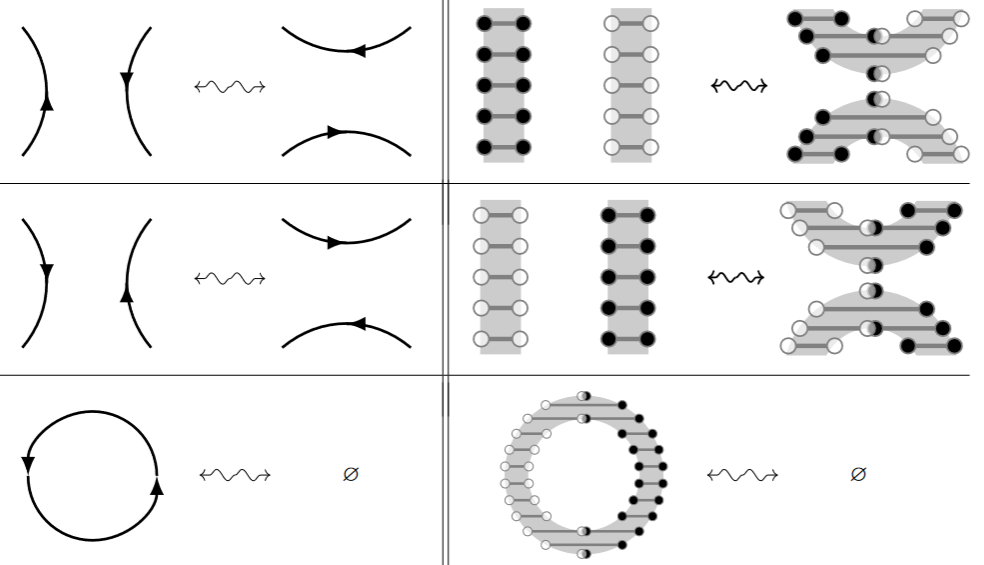
These may be recognized as the birth/death and fusion moves of Khovanov 2000, §6.3, cf. Jacobsson 2004, Fig. 15 and Lobb 2024, Fig. 12 (the latter called saddle point moves by Kauffman 2014, Fig. 16 and others) which (together with diagram isotopy and the Reidemeister moves) generate the link cobordism relation.

Proposition

The vacuum and saddle move imply the 1st Reidemeister move for framed links:

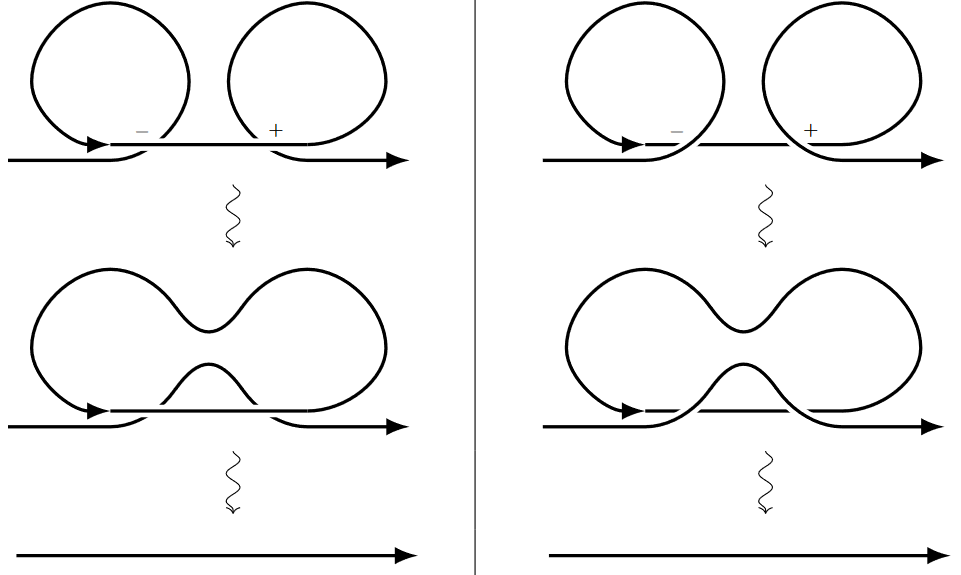
Therefore, regarding framed oriented link diagrams as loops in the Okuyama configuration space descends to a map

(6)$$FrmdOrntdLnk \xrightarrow{\phantom{---}} \pi_1\big( Conf^I(\mathbb{R}^2) \big)$$

from (isotopy classes of) framed oriented links to the fundamental group of the Okuyama configuration space.

Lemma

(Framed links are cobordant to framed unknots)
Every framed link is cobordant (5) to a framed unknot.

Proof

Via the saddle move (5) every crossing (in a given link diagram presentation) of two straight segments may be turned into an avoided crossing of a straight edge and a twisted edge, e.g.:

(7)

Applying this move to all crossings yields a framed unlink. Further forming the connected sum of its connected components as in (4) finally yields a framed unknot.

Theorem

(Charged open string loops classified by crossing number)
Under the identification (3) the map (6)

$$FrmdOrntdLnkDgrms_{/\sim} \xrightarrow{\phantom{---}} \pi_1\big( Conf^I(\mathbb{R}^2) \big) \;\simeq\; \mathbb{Z}$$

is given by sending any framed oriented link diagram to twice its total linking number plus its framing number, hence to the sum of all the entries in its linking matrix.

Proof

By Lem. every link maps to the class of a framed unknot. By the above example (4), any framed unknot is a multiple of the unit framed unknot, which exhibits the latter as a generator

Moreover, since the saddle move used in (7) manifestly preserves the crossing number, that multiple is the crossing number of the original link.

Remark

Besides the 1st Reidemeister move, the 2nd and 3rd also imply the following moves:

Jointly, these moves make the framing number of a framed unknot a well-defined integer, being the sum of the signs of the crossings in any representing link diagram with blackboard framing.

Example

For the Hopf link we get $\pm 2$:

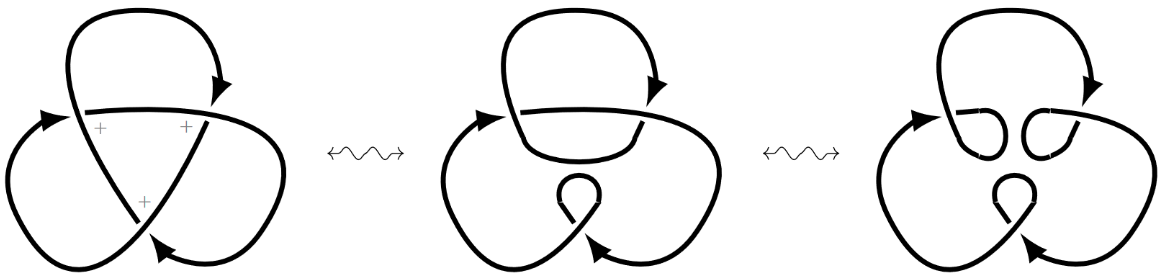
Example

For the trefoil knot we get $\pm 3$:

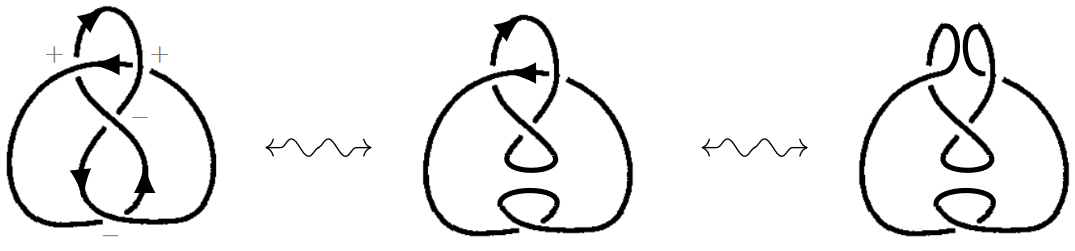
Example

For the figure eight knot we get $0$:

Remark

Under the evident translation between “framing” in the above sense of framed links and normal framing of the underlying 1-dimensional submanifolds in $\mathbb{R}^3$, the above Thm. recovers (from Okuyama’s theorem) the Pontrjagin theorem in these dimensions (cf. Bredon 1993, p. 126).

References

• Graeme Segal, Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973) 213-221 [doi:10.1007/BF01390197, pdf, MR 0331377]

• Dusa McDuff, Configuration spaces of positive and negative particles, Topology 14 1 (1975) 91-107 [doi:10.1016/0040-9383(75)90038-5, pdf]

• Shingo Okuyama: The space of intervals in a Euclidean space, Algebr. Geom. Topol. 5 (2005) 1555-1572 [arXiv:math/0511645, doi:10.2140/agt.2005.5.1555]

The above discussion follows:

• Hisham Sati, Urs Schreiber: Abelian Anyons on Flux-Quantized M5-Branes [arXiv:2408.11896]

After writing this up we learned of the following set of slides, where very similar pictures were already drawn (p. 23-30 and pp. 52):

• Shingo Okuyama: Configuration space of intervals with partially summable labels, talk at Shinshu University (2018) [pdf, pdf]

Precursor discussion of the theorem published as Okuyama 2005:

• Shingo Okuyama: The Space of Intervals and an Approximation to $\Omega^n \Sigma^n X$ (2003) [pdf, pdf]

• Shingo Okuyama: A simple solution for a group completion problem, Trends in Mathematics 7 1 (2004) 69-74 [pdf, pdf]