Schreiber Abelian Anyons on Flux-Quantized M5-Branes

An article that we are finalizing at CQTS:

---

• Hisham Sati$\;$ and $\,$ Urs Schreiber:

  
  

  Abelian Anyons on Flux-Quantized M5-Branes

  
  

  download:

  • pdf (v2)

  • arXiv:2408.11896 (v1)

---

Abstract. While fractional quantum Hall systems provide the best experimental evidence yet of (abelian) anyons plausibly necessary for future fault-tolerant quantum computation, like all strongly-coupled quantum systems their physics is not deeply understood. But, generally a promising approach is to (holographically) realize such systems on branes in string/M-theory; and specifically an old argument by Hellerman & Susskind gives a sketch of fractional quantum Hall states arising via discrete light cone quantization of M5/M9-brane intersections.

Here we present a rigorous derivation of abelian anyon quantum states on M5$\perp$MO9-branes (“open M5-branes”) on the discrete light cone, after globally completing the traditional local field content on the M5-worldvolume via a flux-quantization law compatible with the ambient 11d supergravity, specifically taken to be in unstable unstable co-Homotopy cohomology (“Hypothesis H”).

The main step in the proof uses a theorem of Okuyama to identify co-Homotopy moduli spaces with configuration spaces of strings with charged endpoints, and identifies their loop spaces with cobordism of framed links that, under topological light cone quantization, turn out to be identified with the regularized Wilson loops of abelian Chern-Simons theory.

Followup article:

• Anyons on M5-Probes of Seifert 3-Orbifolds

Related articles.

• Flux Quantization on M5-Branes

• Anyonic defect branes in TED K-theory

• Anyonic topological order in TED K-theory

Talk notes

the success of quantum physics has largely

been rooted in clever perturbation theory

assuming that quantum systems perform

small fluctuations

about a fixed background/mean-field

spectacular success e.g. in

quantum electrodynamics	Landau's Fermi liquid theory

but failure for e.g. in

quantum chromodynamics	anyonic quantum materials
ordinary hadronic matter	e.g. fractional quantum Hall effect

general non-perturbative theory of

strongly coupled/correlated quantum systems

has been largely missing

there are axioms for desiderata (AQFT, FQFT) but little handle on examples

there is computer simulation (lattice models) alongside real experiments

but one potential candidate for

general strongly coupled quantum theory

has been emerging from HE/QG physics:

working title: “M-theory”

general perspective:

quantum systems are modeled (“geometric engineering”)

onto the dynamics of mem-branes (whence “M”)

and higher dimensional “five-branes”

inside an auxiliary higher dim spacetime

popular approach (“holographic duality”):

study quantum dynamics on huge numbers $N \gg 1$

of branes via the gravitational field they source,

this reduces the problem to just classical gravity

eventually more ambitious approach (@ CQTS):

actually formulate the theory for small $N \sim 1$

at least in the relevant topological sectors

namely there was a glaring gap in the literature

with the fields on branes described only locally,

insufficient for seeing solitonic effects like anyons

but it is well known for the electromagnetic field that

its global definition requires a “flux quantization law”

needed to explain e.g. vortex solitons in superconductors

in recent years we developed math of flux quantization

to apply also to the subtle fluxes appearing on M-branes

&

pinpointed candidate flux quantization law for M-theory:

“Hypothesis H”, provably satisfying consistency checks

assuming Hypothesis H, we can derive solitons on branes,

engineering expected effects in quantum materials

in this article we thus quantize the flux on fivebranes &

demonstrate resulting (abelian) anyonic quantum states

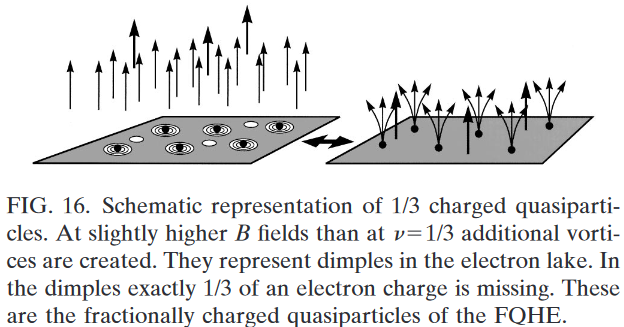
The composite particle (CP) model of the fractional quantum Hall effect (from Störmer 1999):

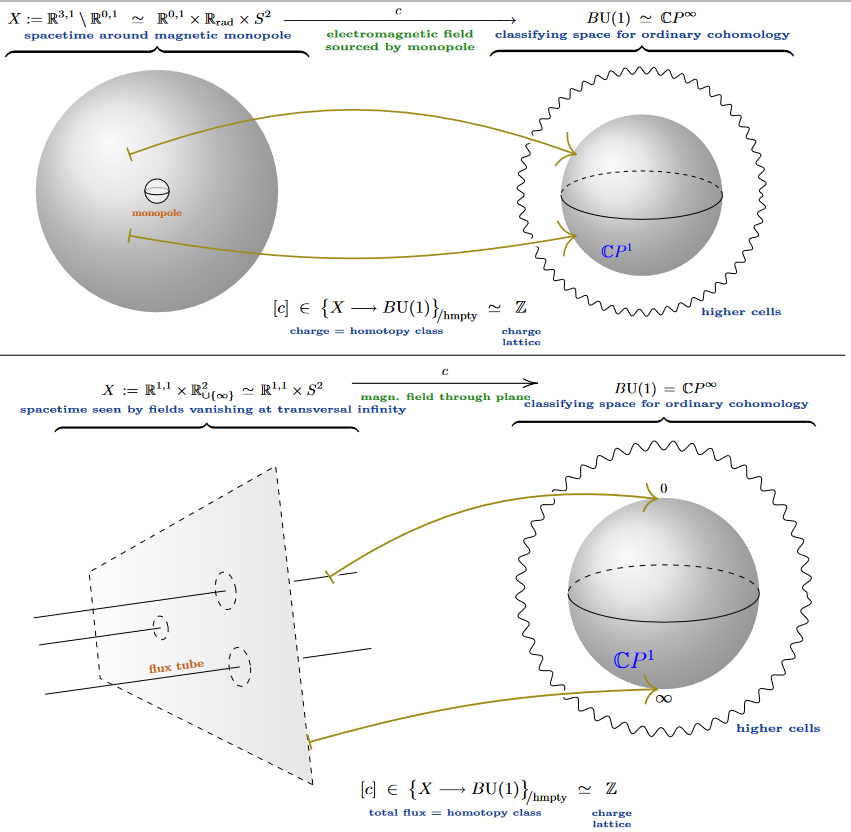
flux quantization of magnetic monopoles & vortices in ordinary cohomology ($K(\mathbb{Z},2)$ $\simeq \mathbb{C}P^\infinity$ ) or 2-Cohomotopy ($\mathbb{C}P^1$):