nLab link cobordism
Context
Knot theory
Examples/classes:
Types
Related concepts:
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Contents
Idea
Link cobordism is a notion of cobordism between links and hence in particular between knots (“knot cobordism”), often considered in higher dimensions (for surface knots etc.)
Beware that some (early) authors require link cobordisms to be cylindrical (see e.g. the first paragraphs of Hosokawa 1967 or in Cappell & Shaneson 1980), hence to be rather what are now called link concordances.
But other authors do mean actual cobordisms when speaking of link cobordism, notably so in the context of Khovanov homology (starting with Khovanov 2000, §6.3, see review in Lobb 2024, Fig 11).
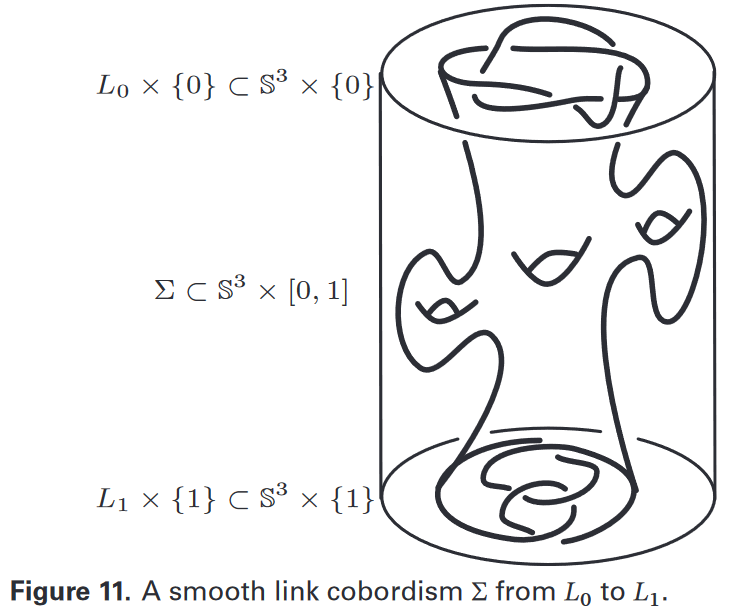
This makes a big difference:
Under actual (framed) cobordism, every (framed) link is (framed) cobordant to a (framed) unlink, in fact to a (framed) unknot.
This follows for instance by the Pontrjagin theorem applied to the 2-Cohomotopy and the fact that this is the free group (generated by the Hopf fibration), with the generator thus corresponding to the unit-framed unknot whose multiples in this group are its connected sums with itself, hence the arbitrarily framed unknots.
More explicitly it follows by applying to every crossing in a link diagram representing a given (blackboard-framed) link the following “fusion” (Khovanov 2000, p. 39) or “saddle” (Kauffman 2014, Fig. 16) cobordism move:
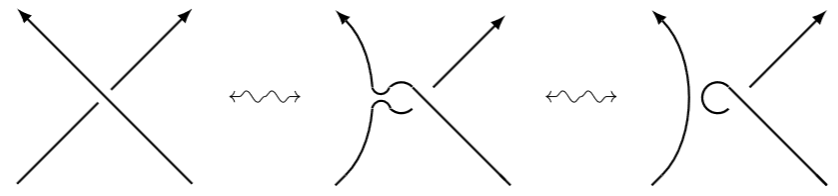
Accordingly, (only) when speaking of link concordance is there any deeper interest in determining the corresponding equivalence classes of links thus related (and this must be meant for instance by Kawauchi 1980), while when speaking of actual link cobordism the interest is more in the characterization of the cobordisms themselves, such as via their associated homomorphism of Khovanov homologies (Jacobsson 2004).
Related concepts
References
On what is really knot/link concordance:
-
Ralph H. Fox, John W. Milnor: Singularities of 2-spheres in 4-space and cobordism of knots, Osaka J. Math. 3 (1966) 257-267 [pdf, pdf, pdf]
-
Fujitsugu Hosokawa: A Concept of Cobordism between Links, Annals of Mathematics 86 2 (1967) 362-373 [doi:10.2307/1970693, jstor:1970693]
-
A. G. Tristram: Some cobordism invariants for links, Proc. Camb. Phil. Soc. 66 (1969) 251-264 [pdf, pdf]
-
Sylvain E. Cappell, Julius L. Shaneson: Link cobordism, Commentarii Mathematici Helvetici 55 (1980) 20–49 [doi:10.1007/BF02566673, pdf]
-
Akio Kawauchi, On links not cobordant to split links, Topology 19 4 (1980) 321-334 [doi:10.1016/0040-9383(80)90017-8]
-
Tim D. Cochran: Geometric invariants of link cobordism, Commentarii Mathematici Helvetici 60 (1985) 291–311 [doi:10.1007/BF02567416]
On actual knot/link cobordism:
- Louis H. Kauffman: §6.3 in: Virtual Knot Cobordism, in: New Ideas in Low Dimensional Topology (2015) 335-377 [arXiv:1409.0324, doi:10.1142/9789814630627_0009]
and specifically in the context of Khovanov homology:
-
Mikhail Khovanov, §6.3 in: A categorification of the Jones polynomial, Duke Math. J. 101 (2000) 359-426 [arXiv:math/9908171, doi:10.1215/S0012-7094-00-10131-7]
(referring to Carter & Saito 1993)
-
Magnus Jacobsson: An invariant of link cobordisms from Khovanov homology, Algebr. Geom. Topol. 4 (2004) 1211-1251 [arXiv:math/0206303, doi:10.2140/agt.2004.4.1211]
reviewed in:
- Andrew Lobb: Figs. 11-12 in: A feeling for Khovanov homology, Notices of the AMS 71 5 (2024) [doi:10.1090/noti2928, pdf, pdf, full issue:pdf]
Last revised on July 25, 2024 at 05:40:49. See the history of this page for a list of all contributions to it.