nLab icosahedron

Idea

(image source)

(image source)

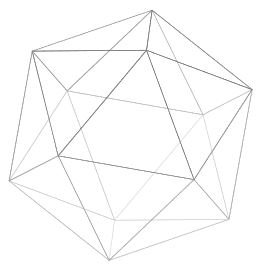
The regular icosahedron is the unique regular convex polyhedron with 20 (triangular) faces. One of the Platonic solids.

Its symmetry group is called the icosahedral group.

$\,$

$\,$

$\,$

$\,$

$\,$

ADE classification and McKay correspondence

Dynkin diagram/ Dynkin quiver	dihedron, Platonic solid	finite subgroups of SO(3)	finite subgroups of SU(2)	simple Lie group
$A_{n \geq 1}$		cyclic group $\mathbb{Z}_{n+1}$	cyclic group $\mathbb{Z}_{n+1}$	special unitary group $SU(n+1)$
A1		cyclic group of order 2 $\mathbb{Z}_2$	cyclic group of order 2 $\mathbb{Z}_2$	SU(2)
A2		cyclic group of order 3 $\mathbb{Z}_3$	cyclic group of order 3 $\mathbb{Z}_3$	SU(3)
A3 = D3		cyclic group of order 4 $\mathbb{Z}_4$	cyclic group of order 4 $2 D_2 \simeq \mathbb{Z}_4$	SU(4) $\simeq$ Spin(6)
D4	dihedron on bigon	Klein four-group $D_4 \simeq \mathbb{Z}_2 \times \mathbb{Z}_2$	quaternion group $2 D_4 \simeq$ Q8	SO(8), Spin(8)
D5	dihedron on triangle	dihedral group of order 6 $D_6$	binary dihedral group of order 12 $2 D_6$	SO(10), Spin(10)
D6	dihedron on square	dihedral group of order 8 $D_8$	binary dihedral group of order 16 $2 D_{8}$	SO(12), Spin(12)
$D_{n \geq 4}$	dihedron, hosohedron	dihedral group $D_{2(n-2)}$	binary dihedral group $2 D_{2(n-2)}$	special orthogonal group, spin group $SO(2n)$, $Spin(2n)$
$E_6$	tetrahedron	tetrahedral group $T$	binary tetrahedral group $2T$	E6
$E_7$	cube, octahedron	octahedral group $O$	binary octahedral group $2O$	E7
$E_8$	dodecahedron, icosahedron	icosahedral group $I$	binary icosahedral group $2I$	E8

References

• Felix Klein, chater I.8 of Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade, 1884, translated as Lectures on the Icosahedron and the Resolution of Equations of Degree Five by George Morrice 1888, online version

• Wikipedia, Icosahedron