nLab SU(3)

Idea

The special unitary group in 3 complex dimensions.

Properties

Subgroups and Supgroups

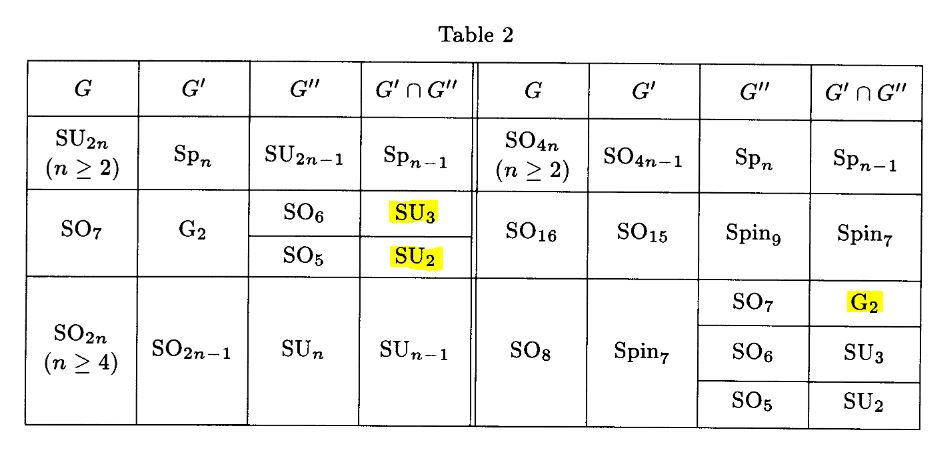
Proposition

We have the following commuting diagram of subgroup inclusions, where each square exhibits a pullback/fiber product, hence an intersection of subgroups:

Here in the bottom row we have the Lie groups

Spin(5)$\hookrightarrow$ Spin(6) $\hookrightarrow$ Spin(7) $\hookrightarrow$ Spin(8)

and in the top row we have

SU(2)$\hookrightarrow$ SU(3) $\hookrightarrow$ G₂ $\hookrightarrow$ Spin(7)

This is a re-statement of Onishchik 93, Table 2, p. 144:

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

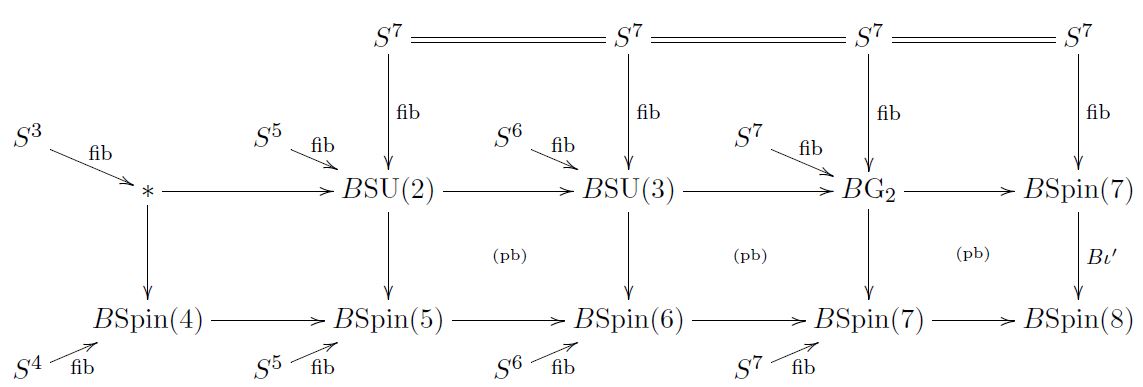
(from FSS 19, 3.4)

$G$-Structure and exceptional geometry

Spin(8)-subgroups and reductions to exceptional geometry

reduction	from spin group	to maximal subgroup
Spin(7)-structure	Spin(8)	Spin(7)
G₂-structure	Spin(7)	G₂
CY3-structure	Spin(6)	SU(3)
SU(2)-structure	Spin(5)	SU(2)
generalized reduction	from Narain group	to direct product group
generalized Spin(7)-structure	$Spin(8,8)$	$Spin(7) \times Spin(7)$
generalized G₂-structure	$Spin(7,7)$	$G_2 \times G_2$
generalized CY3	$Spin(6,6)$	$SU(3) \times SU(3)$

see also: coset space structure on n-spheres

Related concepts

• Calabi-Yau manifold

• U(1), SU(2), SU(4), SU(5)

References

• A. L. Onishchik (ed.) Lie Groups and Lie Algebras

  • I. A. L. Onishchik, E. B. Vinberg, Foundations of Lie Theory,

  • II. V. V. Gorbatsevich, A. L. Onishchik, Lie Transformation Groups

  Encyclopaedia of Mathematical Sciences, Volume 20, Springer 1993

• Howard Georgi, §7 & §9 in: Lie Algebras In Particle Physics, Westview Press (1999), CRC Press (2019) [doi:10.1201/9780429499210]

  with an eye towards application to (the standard model of) particle physics