nLab E6

Idea

One of the exceptional Lie groups.

Properties

As automorphisms of the exceptional Jordan algebra

The group of determinant-preserving linear isomorphisms of the vector space underlying the octonionic Albert algebra is ${E}_{6(-26)}$. (see e.g. (Manogue-Dray 09)).

This may be written as $SL(3,\mathbb{O})$. (Dray-Manogue 09a (16))

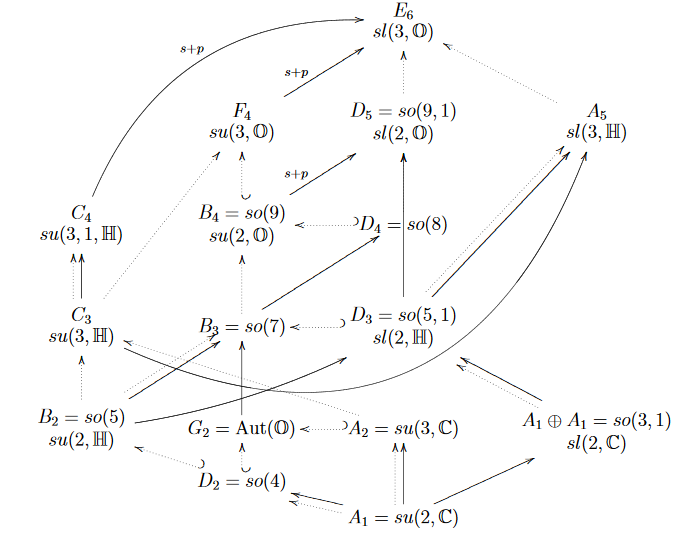
graphics grabbed from (Dray-Manogue 09a, p. 12)

Outer automorphism

The Dynkin diagram of $E_6$ has 2-fold symmetry, corresponding to a nontrivial outer automorphism of order 2. $E_6$ acts on the octonionic projective plane and its outer automorphism gives rise to a projective duality in its geometry.

As part of the ADE pattern

ADE classification and McKay correspondence

Dynkin diagram/ Dynkin quiver	dihedron, Platonic solid	finite subgroups of SO(3)	finite subgroups of SU(2)	simple Lie group
$A_{n \geq 1}$		cyclic group $\mathbb{Z}_{n+1}$	cyclic group $\mathbb{Z}_{n+1}$	special unitary group $SU(n+1)$
A1		cyclic group of order 2 $\mathbb{Z}_2$	cyclic group of order 2 $\mathbb{Z}_2$	SU(2)
A2		cyclic group of order 3 $\mathbb{Z}_3$	cyclic group of order 3 $\mathbb{Z}_3$	SU(3)
A3 = D3		cyclic group of order 4 $\mathbb{Z}_4$	cyclic group of order 4 $2 D_2 \simeq \mathbb{Z}_4$	SU(4) $\simeq$ Spin(6)
D4	dihedron on bigon	Klein four-group $D_4 \simeq \mathbb{Z}_2 \times \mathbb{Z}_2$	quaternion group $2 D_4 \simeq$ Q8	SO(8), Spin(8)
D5	dihedron on triangle	dihedral group of order 6 $D_6$	binary dihedral group of order 12 $2 D_6$	SO(10), Spin(10)
D6	dihedron on square	dihedral group of order 8 $D_8$	binary dihedral group of order 16 $2 D_{8}$	SO(12), Spin(12)
$D_{n \geq 4}$	dihedron, hosohedron	dihedral group $D_{2(n-2)}$	binary dihedral group $2 D_{2(n-2)}$	special orthogonal group, spin group $SO(2n)$, $Spin(2n)$
$E_6$	tetrahedron	tetrahedral group $T$	binary tetrahedral group $2T$	E6
$E_7$	cube, octahedron	octahedral group $O$	binary octahedral group $2O$	E7
$E_8$	dodecahedron, icosahedron	icosahedral group $I$	binary icosahedral group $2I$	E8

As U-duality group of 5d SuGra

$E_6$ is the U-duality group (see there) of 11-dimensional supergravity compactified to 5 dimensions.

	supergravity gauge group (split real form)	T-duality group (via toroidal KK-compactification)	U-duality	maximal gauged supergravity
	$SL(2,\mathbb{R})$	1	$SL(2,\mathbb{Z})$ S-duality	10d type IIB supergravity
	SL$(2,\mathbb{R}) \times$ O(1,1)	$\mathbb{Z}_2$	$SL(2,\mathbb{Z})$ $\times \mathbb{Z}_2$	9d supergravity
SU(3)$\times$ SU(2)	SL$(3,\mathbb{R}) \times SL(2,\mathbb{R})$	$O(2,2;\mathbb{Z})$	$SL(3,\mathbb{Z})\times SL(2,\mathbb{Z})$	8d supergravity
SU(5)	$SL(5,\mathbb{R})$	$O(3,3;\mathbb{Z})$	$SL(5,\mathbb{Z})$	7d supergravity
Spin(10)	$Spin(5,5)$	$O(4,4;\mathbb{Z})$	$O(5,5,\mathbb{Z})$	6d supergravity
E6	$E_{6(6)}$	$O(5,5;\mathbb{Z})$	$E_{6(6)}(\mathbb{Z})$	5d supergravity
E7	$E_{7(7)}$	$O(6,6;\mathbb{Z})$	$E_{7(7)}(\mathbb{Z})$	4d supergravity
E8	$E_{8(8)}$	$O(7,7;\mathbb{Z})$	$E_{8(8)}(\mathbb{Z})$	3d supergravity
E9	$E_{9(9)}$	$O(8,8;\mathbb{Z})$	$E_{9(9)}(\mathbb{Z})$	2d supergravity	E8-equivariant elliptic cohomology
E10	$E_{10(10)}$	$O(9,9;\mathbb{Z})$	$E_{10(10)}(\mathbb{Z})$
E11	$E_{11(11)}$	$O(10,10;\mathbb{Z})$	$E_{11(11)}(\mathbb{Z})$

(Hull-Townsend 94, table 1, table 2)

Related concepts

• exceptional geometry, exceptional generalized geometry

• G2, F4,

  E6, E7, E8, E9, E10, E11, $\cdots$

References

• Tevian Dray, Corinne Manogue, Octonionic Cayley spinors and $E_6$ (pdf)

• Corinne Manogue, Tevian Dray, Octonions, $E_6$, and Particle Physics, J.Phys.Conf.Ser.254:012005,2010 (arXiv:0911.2253)

A description of $E_{6(-26)}$ as the special linear group in dimension 3 with values in the octonions is given in

• Corinne Manogue, Tevian Dray, Octonions and the Structure of $E_6$ Comment. Math. Univ. Carolin., 51:193–207, 2010.

• Aaron Wangberg, Tevian Dray, $E_6$, the Group: The structure of $SL(3,\mathbb{O})$ (arXiv:1212.3182)

Cohomological properties are discussed in

• Mamoru Mimura, Yuriko Sambe, Michishige Tezuka, Cohomology mod 3 of the classifying space of the exceptional Lie group $E_6$, I : structure of Cotor (arXiv:1112.5811),

  Cohomology mod 3 of the classifying space of the exceptional Lie group $E_6$, II : The Weyl group invariants (arXiv:1201.3414)

See also

• Wikipedia, $E_6$