nLab round sphere
Context
Spheres
Riemannian geometry
Contents
Idea
In Riemannian geometry, the topological n-sphere regarded as a Riemannian manifold in the standard way (i.e. as the submanifold of elements at constant distance from a given point in Euclidean space) is also called the round -sphere, in order to distinguish it from other, non-isometric Riemannian manifold structures that also exists on some n-sphere. These alternatives are then also called squashed spheres.
Properties
Proposition
For and , the Ricci tensor of the round -sphere of radius satisfies
for all unit-length tangent vectors , .
Accordingly, the scalar curvature of the round -sphere of radius is the constant function with value
Examples of squashed -spheres
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G₂ is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G₂/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
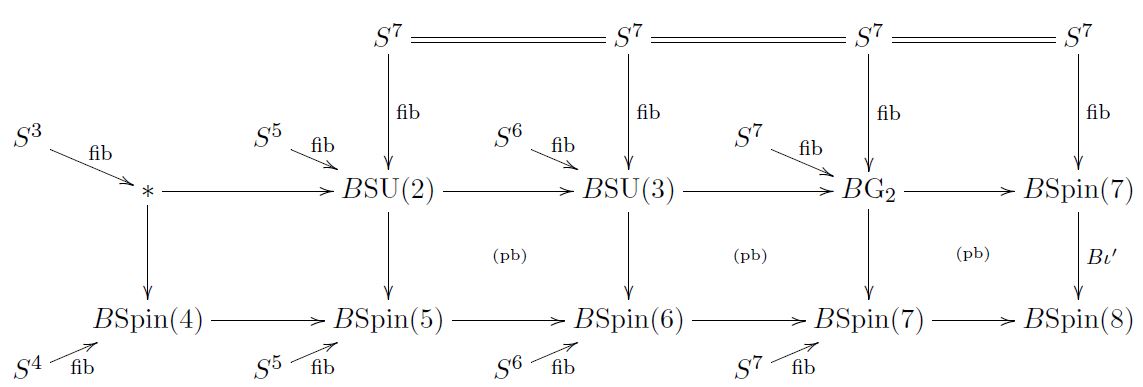
(from FSS 19, 3.4)
Related concepts
Last revised on July 30, 2024 at 13:16:45. See the history of this page for a list of all contributions to it.