Schreiber Topological K-Theory

---

$\,$

What is called topological K-theory is a fundamental construction and tool in the field of topology and homotopy theory. Topological K-theory has an elementary definition but far-reaching applications and results in diverse fields of pure mathematics, as well as in mathematical physics.

In this seminar we work through the basics, starting from general topology as introduced in Introduction to Topology.

$\,$

$\,$

To recall, the subject of topology studies spaces with continuous functions between them: topological spaces, a fundamental concept in all of mathematics. For many applications one cares about the choice of continuous functions only up to continuous deformations, called homotopies. The study of topological spaces with continuous functions up to homotopy is called homotopy theory. Interestingly, this plays an even more fundamental role in mathematics. For some introductory exposition see at Higher Structures in Mathematics and Physics.

In order to study topological spaces up to homotopy – then called homotopy types – a useful strategy is to assign algebraic data to them which may be transferred along continuous functions but is invariant under homotopy: homotopy invariants. This approach to homotopy theory is called algebraic topology.

A basic example of such a homotopy invariant of topological spaces is singular homology and singular cohomology. These are sequences of abelian groups which classify formal formal linear combinations of “singular chains” in a topological space, essentially a simple algebraic way to detect which kind of “holes” there are in a topological space.

But there are more interesting and richer homotopy invariants of topological spaces. In a sense the next example after the “ordinary” singular cohomology is the “generalized cohomology theory” called topological K-theory.

In topological K-theory one detects properties of topological spaces by regarding vector bundles over them. A vector bundle over a topological space $X$ is an assignment of a vector space $V_x$ (the “fiber” over $x$) to each of its points $x \in X$, such that these glue together to one big space $V$ over $X$ as the point $x$ varies in $X$. Hence vector bundles are to be thought of as “continuously varying families of vector spaces”, combining topology with linear algebra.

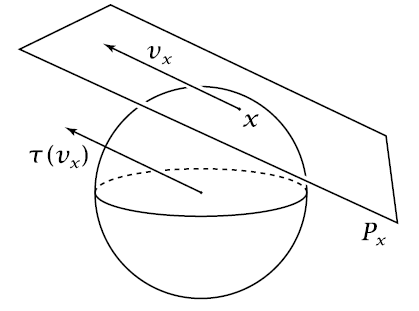
graphics grabbed from Hatcher

For example if $X$ is differentiable, then at each of its points there is a vector space of tangent vectors called the tangent space at that point. The collection of these tangent spaces forms a vector bundle called the tangent bundle. The graphics on the right shows one tangent space to the 2-sphere.

Just as two vector spaces may be combined in their direct sum, so two vector bundles may be combined by point-wise direct sum of their fibers. This makes the isomorphism classes of vector bundles over a fixed topological space form a semi-group (in fact a monoid). The key idea of topological K-theory is to turn this semi-group of vector bundles into an actual (abelian) group by adjoining inverses, a general procedure known as the Grothendieck group construction, after its inventor. Applied to the semi-group of isomorphism classes of vector bundles, this yields the abelian group that is called the topological K-theory group of the underlying topological space. Here the “K” refers to the passage to (isomorphism) classes (German: Klassen).

Topological K-theory studies isomorphism classes of vector bundles over topological spaces together with their formal inverses with respect to direct sum of vector bundles.

$\,$

We now say some of this again, at a slightly more technical level.

$\,$

Recall that for $k$ a field then a $k$-vector bundle over a topological space $X$ is a map $V \to X$ whose fibers are vector spaces which vary over $X$ in a controlled way. Explicitly this means that there exists an open cover $\{U_i \to X\}$ of $X$, a natural number $n \in \mathbb{N}$ (the rank of the vector bundle) and a homeomorphism $U_i \times k^n \to V|_{U_i}$ over $U_i$ which is fiberwise a $k$-linear map.

Vector bundles are of central interest in large parts of mathematics and physics, for instance in Chern-Weil theory and cobordism theory. But the collection $Vect(X)_{/\sim}$ of isomorphism classes of vector bundles over a given space is in general hard to analyze. One reason for this is that these are classified in degree-1 nonabelian cohomology with coefficients in the (nonabelian) general linear group $GL(n,k)$. K-theory may roughly be thought of as the result of forcing vector bundles to be classified by an abelian cohomology theory.

To that end, observe that all natural operations on vector spaces generalize to vector bundles by applying them fiber-wise. Notably there is the fiberwise direct sum of vector bundles, also called the Whitney sum operation. This operation gives the set $Vect(X)_{/\sim}$ of isomorphism classes of vector bundles the structure of an semi-group (monoid) $(Vect(X)_{/\sim},\oplus)$.

Now as under direct sum, the dimension of vector spaces adds, similarly under direct sum of vector bundles their rank adds. Hence in analogy to how one passes from the additive semi-group (monoid) of natural numbers to the addtitive group of integers by adjoining formal additive inverses, so one may adjoin formal additive inverses to $(Vect(X)_{/\sim},\oplus)$. By a general prescription (“Grothendieck group”) this is achieved by first passing to the larger class of pairs $(V_+,V_-)$ of vector bundles (“virtual vector bundles”), and then quotienting out the equivalence relation given by

$$(V_+, V_-) \sim (V_+ \oplus W , V_- \oplus W)$$

for all $W \in Vect(X)_{/\sim}$. The resulting set of equivalence classes is an abelian group with group operation given on representatives by

$$[V_+, V_-] \oplus [V'_+, V'_-] \coloneqq (V_+ \oplus V'_+, V_- \oplus V'_-)$$

and with the inverse of $[V_+,V_-]$ given by

$$-[V_+, V_-] = [V_-, V_+] \,.$$

This abelian group obtained from $(Vect(X)_{/\sim}, \oplus)$ is denoted $K(X)$ and often called the K-theory of the space $X$. Here the letter “K” (due to Alexander Grothendieck) originates as a shorthand for the German word Klasse, referring to the above process of forming equivalence classes of (isomorphism classes) of vector bundles.

This simple construction turns out to yield remarkably useful groups of homotopy invariants. A variety of deep facts in algebraic topology have fairly elementary proofs in terms of topolgical K-theory, for instance

• the proof of topological invariance of dimension;

• the solution of the Hopf invariant one problem (Adams-Atiyah 66),

These proofs make use of the Adams operations on K-theory, which are reflections of the fact that with every vector bundle there is also the exterior tensor powers.

One defines the “higher” K-groups of a topological space to be those of its higher suspensions

$$K^{-n}(X) = K(\Sigma^n X) \,.$$

The assignment $X \mapsto K^\bullet(X)$ turns out to share many properties of the assignment of ordinary cohomology groups $X \mapsto H^n(X,\mathbb{Z})$. One says that topological K-theory is a generalized (Eilenberg-Steenrod) cohomology theory. As such it is represented by a spectrum. For $k = \mathbb{C}$ this is called KU, for $k = \mathbb{R}$ this is called KO. (There is also the unification of both in KR-theory.)

One of the basic facts about topological K-theory, rather unexpected from the definition, is that these higher K-groups repeat periodically in the degree $n$. For $k = \mathbb{R}$ the periodicity is 8, for $k = \mathbb{C}$ it is 2. This is called Bott periodicity. This closely connects to similar periodicities encountered elsewhere in mathematics, notably the periodicity, up to Morita equivalence, of Clifford algebras.

$\,$

Ordinary cohomology

Idea

We are concerned with assigning abelian groups to topological spaces that tell us something about the nature of these spaces, about their “homotopy type”. Before we come to K-theory, the simplest such assignment is called ordinary homology and ordinary cohomology. In its realization as singular chain homology it uses a basic tool of homological algebra to compute these group: chain complexes.

Consider an interval in a topological space $X$, namely a continuous map $\sigma \colon [0,1] \to X$. Its boundary is the two endpoints $\sigma(0) \colon \ast \to X$ and $\sigma(1) \colon \ast \to X$. In order to remember that the first is the “incoming boundary” while the second is the “outgoing boundary” we form their formal difference and call this the oriented boundary

$$\partial \sigma \;\coloneqq\; \sigma(1) - \sigma(0) \,.$$

This suggests that we also allow for signed formal sums $\underset{i}{\sum} a_i \sigma_i$ of intervals in the first place. If all these intervals $\sigma_i$ touch each other at their endpoints, then this looks like a chain of intervals, a 1-dimensional chain, and hence such a formal sum is called a 1-chain, for short. Similarly a formal sum of points is then called a 0-chain. It is natural to extend the boundary operation $\partial$ linearly from intervals to 1-chains. The quotient group

$$H_0(X) \coloneqq \frac{\text{0-chains}}{\text{boundaries of 1-chains}}$$

is called the ordinary homology or singular homology of $X$ in degree 0. Clearly, it is measure for the connected components of $X$. Similarly there are $n$-dimensional chains in $X$, for any $n$, and a boundary map $\partial$ on all of these. It satisfies the fundamental identity that The boundary of a boundary vanishes,

$$\partial \circ \partial = 0 \,.$$

One says that the chains equipped with this nilpotent boundary operation form a chain complex. In general then the quotient group

$$H_n(X) \coloneqq \frac{n\text{-chains that are cycles}}{\text{boundaries of}\; n+1\text{-chains}}$$

is called the ordinary homology of $X$ in degree $n$. This a measure for the “holes of dimension $n$” that one may fund in $X$.

The ordinary homology groups associated with a topological space are homotopy invariants, hence in particular homeomorphism invariants (“topological properties”) that are useful for analyzing, recognizing and and distinguishing topological spaces.

For example the proof of topological invariance of dimension follows by observing that the spaces $\mathbb{R}^{n} \backslash \{0\}$ (Euclidean space minus its origin) have the same ordinary cohomology groups if and only if they have the same dimension $n$.

References

• Allen Hatcher, section 2.1 of Algebraic topology

$\,$

Vector bundles

Idea

For understanding some topological space $X$, it is often useful to understand how another topological space $F$ may be “continuously distributed over” $X$. For instance the two-element space $\{-1, 1\}$ may be continuously distributed over the circle $S^1$ in two inequivalent ways: Either the two points come back to themselves as we move around the circle, or they switch position. This switch is a reflection of the fact that in the circle there are non-contractible loops, in constrast for instance to the 2-sphere, where every loop may be continuously shrunk to a constant loop. If we embed the two points $\{-1,1\}$ into the real line and repeat the construction, then as the line traces around the circle it sweeps out one of two different topological spaces over the circle: either the cylinder (if $+1$ comes back to itself) or the Möbius strip (if $+1$ and $-1$ change position as one goes around the circle).

The image of this situation looks like a “bundle” of “fibers” over the circle. Generally, for $F$ a topological space, then an $F$-fiber bundle over $X$ is another space $E$ with a projection $p \colon E \to X$ that shrinks the fibers away, which all look like $F$ in a controlled way.

For the purpose of topological K-theory we are interested in fibers $F$ which are vector spaces and such that their re-identification as we move around in $X$ is by linear maps. Then one speaks of vector bundles. The theory of vector bundles is much like “continuously parameterized linear algebra”

References

• Hatcher, section 1.1

• Wirthmuller 12, section 1 and section 3

$\,$

Classifying spaces

Idea

Some vector bundles are “tautological”. For consider the topological space of all $k$-dimensional linear subspaces of a fixed $n$-dimensional vector space. Clearly this space carries a vector bundle, namely that whose fiber over the point that labels some subspace is that subspace. It is possible to take this construction and allow $n$ to go to infinity. The result is a classifying space for vector bundles which carries a universal vector bundle: every other vector bundle on a sufficiently well-behaved topological space is classified by a map into this classifying space, namely the map that, roughly, sends each point to the lable of the fiber above it.

References

• Hatcher, section 1.2

• Wirthmuller 12, section 2

• Aguilar-Gitler-Prieto 02, sections 8.3-8-5

$\,$

The K-theory functor

Idea

The isomorphism classes of vector bundles over some topological space $X$ naturally form a semi-group (in fact a monoid) under forming direct sum of vector bundles. But as in ordinary cohomology, we rater want to assign an actual group to $X$, instead of just a semi-group.

There is a universal way to turn a semi-group into an actual group by adjoining formal inverses to all elements. This is called the Grothendieck group construction. Applying this to the semi-group of vector bundles yields “virtual vector bundles”, which are formal differences $[E] - [F]$ of isomorphism classes of actual vector bundles. These now form an abelian group called the topological K-theory group of $X$, and denoted $K(X)$.

Since for every continuous function $f \;\colon\; X \to Y$ and every vector bundle over $Y$ there is the corresponding pullback bundle over $X$, this construction is a (contravariant) functor on the category of topological spaces, just as the ordinary cohomology groups are. In the next session we see that this analogy goes further, so we also call $K(X)$ the K-cohomology group of $X$.

In fact $K(X)$ has more structure than just that of an abelian group. The tensor product of vector bundles makes it a ring. In the next session this will make us say that topological K-theory is a multiplicative cohomology theory.

References

• Wirthmuller 12, sections 6 and 10

• Hatcher, section 2.1

• Aguilar-Gitler-Prieto 02, section 9

$\,$

Generalized cohomology

Idea

We may now make precise in which sense the topological K-theory functor $K(-)$ is directly analogous to the ordinary cohomology functors $H^\bullet(-,\mathbb{Z})$. This involves noticing a list of useful properties satisfied by these functors. In particular one finds that given any continuous function, then it induces a sequence of further continuous functions called its mapping cones and suspensions, and the application of a cohomology functor to these sequences of topological spaces yields long exact sequences in cohomology. This is most useful for computing generalized cohomology groups.

References

• Wirthmuller 12, section 9

• Robert Switzer, chapter 7 (and 8-12) of Algebraic Topology - Homotopy and Homology, Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen, Vol. 212, Springer-Verlag, New York, N. Y., 1975.

$\,$

Clutching construction and Product theorem

Idea

A quick way to construct vector bundles on n-spheres is to consider the trivial vector bundles on either hemisphere and then glue them by a bundle isomorphism on a small overlap of the two hemispheres. This is called the clutching construction. This construction may be paramneterized over some topological space $X$ to construct vector bundles on the product topological space of $X$ with an sphere. A close analysis of this parameterized clutching construction allows to prove what will be the first deep theorem about topological K-theory: the fundamental product theorem in K-theory, which characterizes the $K$-theory ring of product topological spaces $X \times S^2$ of some space $X$ with the 2-sphere as that of $X$ with one generator for the basic line bundle on the 2-sphere adjoined, subject to a relation. This is very useful for computations.

Below this theorem is used to prove the all-important Bott periodicity theorem of topological K-theory.

References

• Wirthmuller 12, p. 17 to p. 29

• Hatcher, p. 41-51

$\,$

Splitting principle

Idea

The second deep fact about topological K-theory is the splitting principle which says roughly that as far as K-theory is concerned, all vector bundles essentially look like direct sums of vector bundles each of whose summands is just a line bundle. This has dramatic consequences, which we see when we discuss the Adams operations below. The proof of the splitting principle involves a careful analysis of flag spaces in vector bundles.

References

Wirthmuller 12, section 10

$\,$

K-Cohomology theory

Idea

Finally we may put all the pieces together and show that the topological K-theory functor $K(-)$ indeed constitutes a generalized (Eilenberg-Steenrod) cohomology theory. In fact its ring structure makes it a multiplicative cohomology theory. Moreover, we find that the fundamental product theorem in K-theory implies a certain 2-periodicity in $K(-)$, called Bott periodicity. This makes $K$ an even periodic cohomology theory.

All these facts will be most useful for computing $K(X)$ and for using it to learn about topological spaces which is what we turn to next.

References

• Wirthmuller 12, p. 34 and previous

• Hatcher, section 2.2

• Aguilar-Gitler-Prieto 02, appendix B

$\,$

Examples of K-groups

Idea

In the previous sessions we have accumulated some powerful tools for computing topological K-theory groups. Here we use these to consider examples, and compute K-theory groups for a range of interesting topological spaces. This will serve to see how topological K-theory is a finer invariant than ordinary cohomology.

References

• Chris Blair, Some K-theory examples, 2009 (pdf)

$\,$

Adams operations

Idea

So far we have used that there is the operation of direct sum of vector bundles and of tensor product of vector bundles in order to exhibit the $K$-theory functor $K(-)$ as taking values in commutative rings. But in fact there are yet more operations on vector bundles. Namely instead of just taking plain tensor products, we may also form skew-symmetrized tensor products exterior products. Since these are traditionally denoted $\wedge^n(-)$, one says that $K(-)$ inherits the structure of a Lambda-ring. A clever combination of such exterior powers makes them be an abelian group homomorphism, these are the Adams operations on topological K-theory. We observe their basic properties, which make them most useful for characterizing topological spaces. As a first example we see that they immediately allow to prove something as fundamental to topology as the topological invariance of dimension.

An even more interesting application of the Adams operations is that they allow to characterite the continuous functions of Hopf invariant one. This is the next topic.

References

• Wirthmuller 12, section 11

• Hatcher, section 2.3

• Aguilar-Gitler-Prieto 02, section 10

$\,$

Hopf invariant one

Idea

A crown jewel of the application of topological K-theory, is, via the Adams operations, a remarkably quick proof of a deep theorem whose original solution via another tool (the Adams spectral sequence) marks the beginning of modern homotopy theory: the Hopf invariant one problem.

A remarkable range of “exceptional” structures in mathematics is obtained by continuing the step from the real numbers to the complex numbers further to find the quaternions and then the octonions. Using the fact that all these algebras are real normed division algebras they induce fibrations between spheres: the Hopf fibrations.

These Hopf fibrations happen to take value +1 in a certain invariant, called the Hopf invariant. The Hopf invariant one theorem says that they there is in fact no other fibration with this property. In particular this implies, remarkably, that the real numbers, complex numbers, quaternions and octonions are the only real normed division algebras that exist.

References

• Hatcher, section 2.3

• Wirthmuller 12, section 12

• Aguilar-Gitler-Prieto 02, section 10.6

$\,$

Equivariant K-theory

Idea

We saw how topological K-theory arises from pairing topology with linear algebra. There are variaous further refinements of topological K-theory obtained by refining these ingredients. In particular, if instead of plain vector spaces we start by considering vector spaces equipped with linear group actions, hence considering linear representations, then the resulting topological K-theory is what is called equivariant K-theory. This now pairs topology with representation theory. For instance this may now be evaluated on topological spaces which are themselves acted on by groups, and the resulting equivariant K-theory groups encode interesting information for instance about the fixed point loci of these group actions.

References

• Wirthmuller 12, section 14

$\,$

$(\star)$ The K-theory spectrum

This section goes beyond an introduction, in that it requires more tools from algebraic topology. We include it for completeness and as outlook.

Idea

While we constructed classifying spaces originally for plain vector bundles, one finds that with just slight modification these also yield classifying space for virtual vector bundles, hence for topological K-theory. The fact that topological K-theory constitutes a generalized (Eilenberg-Steenrod) cohomology theory with long exact sequences in cohomology now implies that also these classifying spaces arrange in certain sequences. Suchsequences are called sequential spectra or just spectra, for short, and the spectrum that represents topoligcal K-theory of complex vector bundles is called KU.

The main point in its construction is the incarnation of Bott periodicity in terms of the classifying spaces. This yields an alternative proof of Bott periodicity, one that makes use of basics of the classical model structure on topological spaces.

References

• Aguilar-Gitler-Prieto 02, appendix B.2

$\,$

References

• Klaus Wirthmüller,

  Vector bundles and K-theory (2012)

  (ftp://www.mathematik.uni-kl.de/pub/scripts/wirthm/Top/vbkt_skript.pdf)

• Allen Hatcher,

  Vector bundles & K-theory

  (https://www.math.cornell.edu/~hatcher/VBKT/VBpage.html)

• Marcelo Aguilar, Samuel Gitler, Carlos Prieto,

  Algebraic topology from a homotopical viewpoint,

  Springer (2002)