nLab Introduction to Topology
This page contains a detailed introduction to basic topology. Starting from scratch (required background is just a basic concept of sets), and amplifying motivation from analysis, it first develops standard point-set topology (topological spaces). In passing, some basics of category theory make an informal appearance, used to transparently summarize some conceptually important aspects of the theory, such as initial and final topologies and the reflection into Hausdorff and sober topological spaces. We close with discussion of the basics of topological manifolds and differentiable manifolds, laying the foundations for differential geometry. The second part introduces some basics of homotopy theory, mostly the fundamental group, and ends with their first application to the classification of covering spaces.
Lecture notes. (web version requires Firefox browser – free download)
part I: Introduction to Topology 1 – Point-set Topology (pdf 203p)
part II: Introduction to Topology 2 – Basic Homotopy Theory (pdf 61p)
For introduction to abstract homotopy theory see instead at Introduction to Homotopy Theory.
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
The idea of topology is to study “spaces” with “continuous functions” between them. Specifically one considers functions between sets (whence “point-set topology”, see below) such that there is a concept for what it means that these functions depend continuously on their arguments, in that their values do not “jump”. Such a concept of continuity is familiar from analysis on metric spaces, (recalled below) but the definition in topology generalizes this analytic concept and renders it more foundational, generalizing the concept of metric spaces to that of topological spaces.
Hence, topology is the study of the category whose objects are topological spaces, and whose morphisms are continuous functions. This category is much more flexible than that of metric spaces, for example it admits the construction of arbitrary quotients and intersections of spaces. Accordingly, topology underlies or informs many and diverse areas of mathematics, such as functional analysis, operator algebra, manifold/scheme theory, hence algebraic geometry and differential geometry, and the study of topological groups, topological vector spaces, local rings, etc. Not the least, it gives rise to the field of homotopy theory, where one considers also continuous deformations of continuous functions themselves (“homotopies”). Topology itself has many branches, such as low-dimensional topology or topological domain theory.
A popular imagery for the concept of a continuous function is provided by deformations of elastic physical bodies, which may be deformed by stretching them without tearing. The canonical illustration is a continuous bijective function from the torus to the surface of a coffee mug, which maps half of the torus to the handle of the coffee mug, and continuously deforms parts of the other half in order to form the actual cup. Since the inverse function to this function is itself continuous, the torus and the coffee mug, both regarded as topological spaces, are “the same” for the purposes of topology; one says they are homeomorphic.
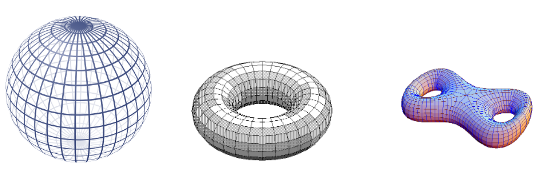
On the other hand, there is no homeomorphism from the torus to, for instance, the sphere, signifying that these represent two topologically distinct spaces. Part of topology is concerned with studying homeomorphism-invariants of topological spaces (“topological properties”) which allow to detect by means of algebraic manipulations whether two topological spaces are homeomorphic (or more generally homotopy equivalent) or not. This is called algebraic topology. A basic algebraic invariant is the fundamental group of a topological space (discussed below), which measures how many ways there are to wind loops inside a topological space.
Beware the popular imagery of “rubber-sheet geometry”, which only captures part of the full scope of topology, in that it invokes spaces that locally still look like metric spaces (called topological manifolds, see below). But the concept of topological spaces is a good bit more general. Notably, finite topological spaces are either discrete or very much unlike metric spaces; the former play a role in categorical logic. Also, in geometry, exotic topological spaces frequently arise when forming non-free quotients. In order to gauge just how many of such “exotic” examples of topological spaces beyond locally metric spaces one wishes to admit in the theory, extra “separation axioms” are imposed on topological spaces (see below), and the flavour of topology as a field depends on this choice.
Among the separation axioms, the Hausdorff space axiom is the most popular (see below). But the weaker axiom of sobriety (see below) stands out, because on the one hand it is the weakest axiom that is still naturally satisfied in applications to algebraic geometry (schemes are sober) and computer science (Vickers 89), and on the other, it fully realizes the strong roots that topology has in formal logic: sober topological spaces are entirely characterized by the union-, intersection- and inclusion-relations (logical conjunction, disjunction and implication) among their open subsets (propositions). This leads to a natural and fruitful generalization of topology to more general “purely logic-determined spaces”, called locales, and in yet more generality, toposes and higher toposes. While the latter are beyond the scope of this introduction, their rich theory and relation to the foundations of mathematics and geometry provide an outlook on the relevance of the basic ideas of topology.
Point-set Topology
This chapter is at Introduction to Topology 1 – Point-set Topology
Basic Homotopy Theory
This chapter is at Introduction to Topology 1 – Basic Homotopy Theory
References
Point-Set Topology
General
A canonical compendium is
- Nicolas Bourbaki, chapter 1 Topological Structures in Elements of Mathematics III: General topology, Springer (1971, 1990)
Introductory textbooks include
-
John Kelley, General Topology, Graduate Texts in Mathematics, Springer (1955)
-
James Munkres, Topology, Prentice Hall (1975, 2000)
Lecture notes include
- Friedhelm Waldhausen, Topologie (pdf)
See also the references at algebraic topology.
Special topics
The standard literature typically omits the following important topics:
Discussion of sober topological spaces is briefly in
- Peter Johnstone, section II 1. of Stone Spaces, Cambridge Studies in Advanced Mathematics 3, Cambridge University Press 1982. xxi+370 pp. MR85f:54002, reprinted 1986.
An introductory textbook that takes sober spaces, and their relation to logic, as the starting point for topology is
- Steven Vickers, Topology via Logic, Cambridge University Press (1989)
Detailed discussion of the Hausdorff reflection is in
- Bart van Munster, The Hausdorff quotient, 2014 (pdf)
Basic homotopy theory
A textbook account is in
- Tammo tom Dieck, sections 2 an 3 of Algebraic Topology, EMS 2006 (pdf)
Lecture notes include
- Jesper Møller, The fundamental group and covering spaces (2011) (pdf)
Last revised on March 6, 2019 at 22:36:36. See the history of this page for a list of all contributions to it.