nLab MUFr

Idea

In joint generalization of the cobordism cohomology theories MU and MFr of closed $U$-manifolds and of $Fr$-manifolds, respectively, a $(U,fr)$-manifold (Conner-Floyd 66, Section 16, Conner-Smith 69, Sections 6, 13) is a compact manifold with boundary equipped with unitary group-tangential structure on its stable tangent bundle and equipped with a trivialization (stable framing) of that over the boundary.

The corresponding bordism classes form a bordism ring denoted $\Omega^{\mathrm{U},fr}_\bullet$.

Properties

Representing spectrum

In generalization to how the complex cobordism ring $\Omega^U_{2k}$ is represented by homotopy classes of maps into the Thom spectrum MU, so $\Omega^{\mathrm{U},fr}_{2k}$ is represented by maps into the quotient spaces $MU_{2k}/S^{2k}$ (for $S^{2k} = Th(\mathbb{C}^{k}) \to Th( \mathbb{C}^k \times_{\mathrm{U}(k)} E \mathrm{U}(k) ) = M \mathrm{U}_{2k}$ the canonical inclusion):

(1)$$\Omega^{(\mathrm{U},fr)}_\bullet \;=\; \pi_{\bullet + 2k} \big( MU_{2k}/S^{2k} \big) \,, \;\;\;\;\; \text{for any} \; 2k \geq \bullet + 2 \,.$$

(Conner-Floyd 66, p. 97)

Hence the representing spectrum $M(\mathrm{U},fr)$ is the homotopy cofiber of the ring spectrum unit $1^{M\mathrm{U}} \;\colon\; \mathbb{S} \longrightarrow M \mathrm{U}$ out of the sphere spectrum (Conner-Smith 69, p. 156 (41 of 106), Smith 71) which deserves to be denoted

$$M(\mathrm{U},fr) \;\coloneqq\; M \mathrm{U} / \mathbb{S} \,,$$

but which in notation common around the Adams spectral sequence would be “$\Sigma \overline {M \mathrm{U}}$” (as in Adams 74, theorem 15.1 page 319) or just “$\overline{ M \mathrm{U} }$” (e.g. Hopkins 99, Cor. 5.3):

(2)$$\array{ \mathbb{S} & \overset{ 1^{M\mathrm{U}} }{ \longrightarrow } & M \mathrm{U} \\ \big\downarrow & {}^{{}_{(po)}} & \big\downarrow \\ \ast &\longrightarrow& M \mathrm{U}/ \mathbb{S} }$$

So in terms of stable homotopy groups of this spectrum we have the $(\mathrm{U},fr)$-cobordism ring

(3)$$\Omega^{\mathrm{U},fr}_{\bullet} \;\coloneqq\; \pi_{\bullet} \big( M\mathrm{U}/\mathbb{S} \big)$$

Boundary morphism to $MFr$

The realization (2) makes it manifest (this is left implicit in Conner-Floyd 66, p. 99) that there is a cohomology operation to MFr of the form

(4)$$\array{ M(\mathrm{U},fr) \;= & M \mathrm{U}/\mathbb{S} & \overset{ \;\;\; \partial \;\;\; }{\longrightarrow} & \Sigma \mathbb{S} & =\; \Sigma Mfr \\ \pi_{2d+2}\big( M(\mathrm{U},fr) \big) && \longrightarrow && \pi_{2d+1}\big( Mfr \big) } \,.$$

Namely, $\partial$ is the second next step in the long homotopy cofiber-sequence starting with $1^{M \mathrm{U}}$. In terms of the pasting law:

(5)$$\array{ \mathbb{S} & \overset{ 1^{M\mathrm{U}} }{ \longrightarrow } & M \mathrm{U} & \longrightarrow & \ast \\ \big\downarrow & {}^{{}_{(po)}} & \big\downarrow & {}^{{}_{(po)}} & \big\downarrow \\ \ast & \longrightarrow & M \mathrm{U}/ \mathbb{S} & \underset{ \partial }{ \longrightarrow } & \Sigma \mathbb{S} }$$

Remark

The implicit idea in Conner-Floyd 66, p. 99 must be to see $\partial$ (4) in terms of forming actual boundaries of representative manifolds with boundaries under a version of the Pontrjagin-Thom construction. This is certainly plausible, but not proven either, as they “forego the tedious details” on p. 97. NB: for the purpose on p. 99 they might just define $\partial$ in this geometric way, but then the claim wrapping around p. 100-101 needs proof. This claim however is immediate from the abstract homotopy theory, namely it is just the continuation yet one step further along the long cofiber sequence – this is Prop. below.

Relation to $MU$ and $MFr$

Proposition

In positive degree, the underlying abelian groups of the bordism rings for MU, MFr and $MUFr$ (3) sit in short exact sequences of this form:

(6)$$0 \to \Omega^{\mathrm{U}}_{2n + 2} \overset{i}{\longrightarrow} \Omega^{\mathrm{U},fr}_{2n + 2} \overset{\partial}{ \longrightarrow } \Omega^{fr}_{2n + 1} \to 0 \,, \phantom{AAAA} n \in \mathbb{N} \,,$$

where $i$ is the evident inclusion, while $\partial$ is the boundary homomorphism from above.

This is stated without comment in Conner-Floyd 66, p. 99. The beginning of an argument appears inside the proof of CF66, Thm. 16.2 (p. 100), attributed there to Peter Landweber (see Remark below). The idea for how to complete the argument is a little more explicit in Stong 68, p. 102.

The following is the complete and quick proof using the formulation (5) via abstract homotopy above:

Proof

We have the long exact sequence of homotopy groups (long exact sequence in generalized cohomology on spheres) obtained from the cofiber sequence $\mathbb{S} \overset{1^{M\mathrm{U}}}{\longrightarrow} M \mathrm{U} \to M \mathrm{U}/\mathbb{S} \overset{\partial}{\to} \Sigma \mathbb{S}$ (5), the relevant part of which looks as follows:

(7)$$\array{ \overset{ \mathclap{ \color{darkblue} pure \; torsion } }{ \overbrace{ \pi_{2d+2} \big( \mathbb{S} \big) } } & \overset{ 1^{M\mathrm{U}} }{ \longrightarrow } & \overset{ \mathclap{ \color{darkblue} free \; abelian } }{ \overbrace{ \pi_{2d+2} \big( M\mathrm{U} \big) } } & \overset{ }{\longrightarrow} & \pi_{2d+2} \big( M\mathrm{U}/\mathbb{S} \big) & \overset{ \partial }{\longrightarrow} & \pi_{2d+1}\big(\mathbb{S}\big) &\longrightarrow& \overset{ \color{darkblue} trivial }{ \overbrace{ \pi_{2d+1}\big(M\mathrm{U}\big) } } \\ \big\downarrow{}^{\mathrlap{=}} && \big\downarrow{}^{\mathrlap{=}} && \big\downarrow{}^{\mathrlap{=}} && \big\downarrow{}^{\mathrlap{=}} && \big\downarrow{}^{\mathrlap{=}} \\ \Omega^{fr}_{2d+2} & \underset{ \color{green} 0 }{ \longrightarrow } & \Omega^{\mathrm{U}}_{2d+2} & \underset{ i }{\longrightarrow} & \Omega^{(\mathrm{U},fr)}_{2d+2} & \underset{ \partial }{\longrightarrow} & \Omega^{fr}_{2d + 1} & \underset{ \color{green} 0 }{\longrightarrow} & 0 }$$

Observing now that the stable homotopy groups of $M\mathrm{U}$ are free abelian groups concentrated in even degrees (by this theorem at MU) it follows that:

1. the rightmost morphism shown in (7) is the zero morphism since its codomain is zero;

2. the leftmost morphism shown in (7) is the zero morphism, since the stable homotopy groups of spheres are all pure torsion groups in positive degrees (by the Serre finiteness theorem), and the only morphism from a torsion group to a free abelian group is the zero morphism.

Remark

Here is an explicit construction of a lift through the boundary map in (6), depending on a choice of trivialization in $\pi_{2d-1}\big( M\mathrm{U}\big)$:

(The following is essentially a streamlined account of the construction in the first half of the proof of Conner-Floyd 66, Thm. 16.2; for more and a more abstract perspective see at d-invariant the section Trivializations of the d-invariant):

Let

$$\big[ \Sigma^\infty S^{2(n+d)-1} \overset{ \Sigma^{\infty} {\color{green} c } }{\longrightarrow} \Sigma^\infty S^{2n} \big] \;\in\; \pi^s_{2d-1} \;\simeq\; \Omega^{fr}_{2d-1}$$

be a given class in stable Cohomotopy, hence in the MFr-cobordism ring, under the PT isomorphism. (We write this as the stabilization of a class ${\color{green} c}$ in unstable Cohomotopy just for emphasis that we can.)

Consider then following homotopy pasting diagram:

From SS21

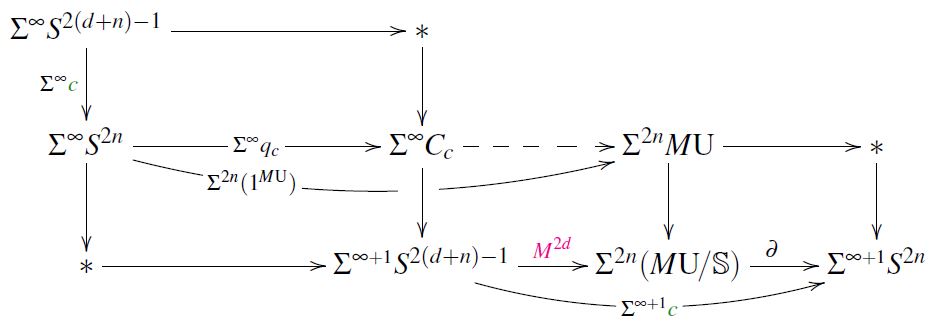
Here all squares are homotopy pushout-squares, they arise as follows (beware that we say “square” for any single cell and “rectangle” for the pasting composite of any adjacent pair of cells):

• The top square witnesses the homotopy cofiber $C_c$, defined thereby;

• the left rectangle is a homotopy pushout by definition of suspension,

• hence the bottom left square is so by the pasting law.

• Again via the first point, a dashed morphism exists as shown, witnessing the fact that the pullback of the class $\Sigma^{2n}(1^{M\mathrm{U}})$ to an odd-dimensional square vanishes (as does every $MU$-class);

• with this, the bottom left rectangle exists, and it is a homotopy pushout by definition of $M \mathrm{U}/\mathbb{S}$ (5);

• hence the morphism $\color{magenta} M^{2 d}$ exists, and the resulting bottom middle square is a homotopy pushout, again by the pasting law.

• Now the bottom right rectangle is defined to be a homotopy pushout, and thus looks as shown by the pasting law;

• therefore the bottom right square exists, and it is a homotopy pushout by the pasting law.

But now the commuting three morphism in the very bottom and right part of the diagram shows that ${\color{magenta}M^{2d}} \in \pi_{2d}\big( M(U,fr) \big)$ is a lift of ${\color{green} c} \in \pi_{2d-1}(M Fr)$ through $\partial$.

Relation to Todd classes and the e-invariant

Proposition

(e-invariant is Todd class of cobounding (U,fr)-manifold)

Evaluation of the Todd class on $(U,fr)$-manifolds yields rational numbers which are integers on actual $U$-manifolds. It follows with the short exact sequence (6) that assigning to $Fr$-manifolds the Todd class of any of their cobounding $(U,fr)$-manifolds yields a well-defined element in Q/Z.

Under the Pontrjagin-Thom isomorphism between the framed bordism ring and the stable homotopy group of spheres $\pi^s_\bullet$, this assignment coincides with the Adams e-invariant in its Q/Z-incarnation:

(8)$$\array{ 0 \to & \Omega^{\mathrm{U}}_{\bullet+1} & \overset{i}{\longrightarrow} & \Omega^{\mathrm{U},fr}_{\bullet+1} & \overset{\partial}{ \longrightarrow } & \Omega^{fr}_\bullet & \simeq & \pi^s_\bullet \\ & \big\downarrow{}^{\mathrlap{Td}} && \big\downarrow{}^{\mathrlap{Td}} && \big\downarrow{}^{} && \big\downarrow{}^{e} \\ 0 \to & \mathbb{Z} &\overset{\;\;\;\;\;}{\hookrightarrow}& \mathbb{Q} &\overset{\;\;\;\;}{\longrightarrow}& \mathbb{Q}/\mathbb{Z} &=& \mathbb{Q}/\mathbb{Z} } \,,$$

(Conner-Floyd 66, Theorem 16.2)

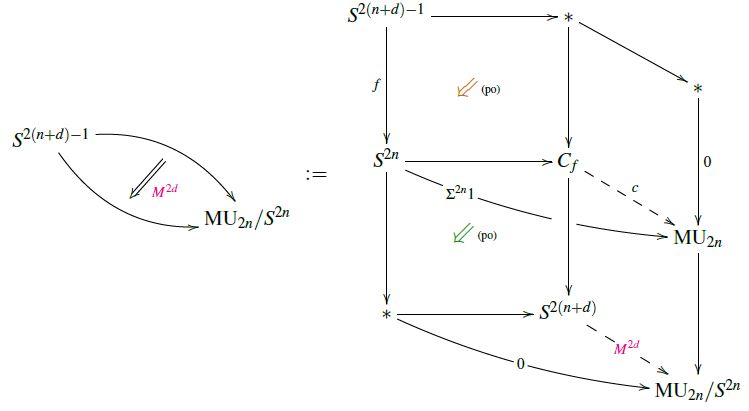
The first step in the proof of (8) is the observation (Conner-Floyd 66, p. 100-101) that the representing map (1) for a $(U,fr)$-manifold $M^{2k}$ cobounding a $Fr$-manifold represented by a map $f$ is given by the following homotopy pasting diagram (see also at Hopf invariant – In generalized cohomology):

from SS21

Related concepts

flavors of bordism homology theories/cobordism cohomology theories, their representing Thom spectra and cobordism rings:

bordism theory$\;$M(B,f) (B-bordism):

• MFr

• MO, MSO, MSpin, MString, …

• MU, MSU, …

  MΩΩSU(n)

  MP, MR

• MSpin^c

• MSp

relative bordism theories:

• MOFr, MUFr, MSUFr

equivariant bordism theory:

• equivariant MFr

• equivariant MO

• equivariant MU

global equivariant bordism theory:

• global equivariant mO,

• global equivariant mU

algebraic:

• algebraic cobordism

References

The concept of $(U,fr)$-bordism theory and its relation to the e-invariant originates with:

• Pierre Conner, Edwin Floyd, Section 16 of: The Relation of Cobordism to K-Theories, Lecture Notes in Mathematics 28 Springer 1966 (doi:10.1007/BFb0071091, MR216511)

• Pierre Conner, Larry Smith, Section 6 of: On the complex bordism of finite complexes, Publications Mathématiques de l’IHÉS, Tome 37 (1969) , pp. 117-221 (numdam:PMIHES_1969__37__117_0)

Analogous discussion for MO-bordism with MSO-boundaries:

• G. E. Mitchell, Bordism of Manifolds with Oriented Boundaries, Proceedings of the American Mathematical Society Vol. 47, No. 1 (Jan., 1975), pp. 208-214 (doi:10.2307/2040234)

Analogous discussion for MOFr is in

• Robert Stong, p. 102 of: Notes on Cobordism theory, Princeton University Press, 1968 (toc pdf, ISBN:9780691649016, pdf)

See also

• Larry Smith, On characteristic numbers of almost complex manifolds with framed boundaries, Topology Volume 10, Issue 3, August 1971, Pages 237-256 (doi:10.1016/0040-9383(71)90008-5)

Generalization to manifolds with corners and relation to the f-invariant:

• Gerd Laures, On cobordism of manifolds with corners, Trans. Amer. Math. Soc. 352 (2000) (doi:10.1090/S0002-9947-00-02676-3)