nLab The Multifaceted Skyrmion
This page collectes material related to the book
-
Mannque Rho, Ismail Zahed (eds.)
The Multifaceted Skyrmion,
World Scientific
Second edition, 2016
on Skyrmions, particularly as a model for confinement in QCD of quarks within hadrons (but also in solid state physics) and their origin as instantons of a holographic 5d Yang-Mills theory (holographic QCD, AdS/QCD correspondence).
Contents
Introduction
- Mannque Rho et al., Introduction
One can make chiral perturbation theory consistent with QCD by suitably matching the correlators of the effective theory to those of QCD at a scale near . Clearly this procedure is not limited to only one set of vector mesons; in fact, one can readily generalize it to an infinite number of hidden gauge fields in an effective Lagrangian. In so doing, it turns out that a fifth dimension is “deconstructed” in a (4+1)-dimensional (or 5D) Yang–Mills type form. We will see in Part III that such a structure arises, top-down, in string theory.
this holographic QCD model comes out to describe — unexpectedly well — low-energy properties of both mesons and baryons, in particular those properties reliably described in quenched lattice QCD simulations.
One of the most noticeable results of this holographic model is the first derivation of vector dominance (VD) that holds both for mesons and for baryons. It has been somewhat of an oddity and a puzzle that Sakurai's vector dominance — with the lowest vector mesons ρ and ω — which held very well for pionic form factors at low momentum transfers famously failed for nucleon form factors. In this holographic model, the VD comes out automatically for both the pion and the nucleon provided that the infinite KK-tower is included. While the VD for the pion with the infinite tower is not surprising given the successful Sakurai VD, that the VD holds also for the nucleons is highly nontrivial. It turns out to be a consequence of a holographic Cheshire Cat phenomenon
Hadrons and Nuclear Matter
Chapter 1
On Skyrmions as models for atomic nuclei all the way up to carbon:
- Richard A. Battye, Nicholas Manton, Paul Sutcliffe, Skyrmions and Nuclei, pp. 3-39 (2010) (doi:10.1142/9789814280709_0001)
Chapter 2
- Gottfried Holzwarth, Electromagnetic Form Factors of the Nucleon in Chiral Soliton Models (arXiv:hep-ph/0511194), Chapter 2 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Chapter 3
- Dmitri Diakonov, Victor Petrov, Exotic baryon resonances in the Skyrme model (arXiv:0812.1212, doi:10.1142/9789814704410_0004), Chapter 3 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
It is astounding that Skyrme had suggested his model as early as in 1961 before it has been generally accepted that pions are (pseudo) Goldstone bosons associated with the spontaneous breaking of chiral symmetry, and of course long before Quantum Chromodynamics (QCD) has been put forward as the microscopic theory of strong interactions.
The revival of the Skyrme idea in 1983 is due to Witten who explained the raison d’ˆetre of the Skyrme model from the viewpoint of QCD. In the chiral limit when the light quark masses , , tend to zero, such that the octet of the pseudoscalar mesons π, K , η become nearly massless (pseudo) Goldstone bosons, they are the lightest degrees of freedom of QCD. The effective chiral Lagrangian (EχL) for pseudoscalar mesons, understood as an infinite expansion in the derivatives of the pseudoscalar (or chiral) fields, encodes, in principle, full information about QCD. The famous two-term Skyrme Lagrangian can be understood as a low-energy truncation of this infinite series. Witten has added an important four-derivative Wess–Zumino term to the original Skyrme Lagrangian and pointed out that the overall coefficient in front of the EχL is proportional to the number of quark colours .
Soon after Witten’s work it has been realized that it is possible to bring the Skyrme model and the Skyrmion even closer to QCD and to the more customary language of constituent quarks. It has been first noticed 6, 7a, 7b, 8 that a simple chiral invariant Lagrangian for massive (constituent) quarks interacting with the octet chiral field ,
induces, via a quark loop in the external pseudoscalar fields (see Fig. 3.1), the EχL whose lowest-derivative terms coincide with the Skyrme Lagrangian, including automatically the Wess–Zumino term, with the correct coefficient!
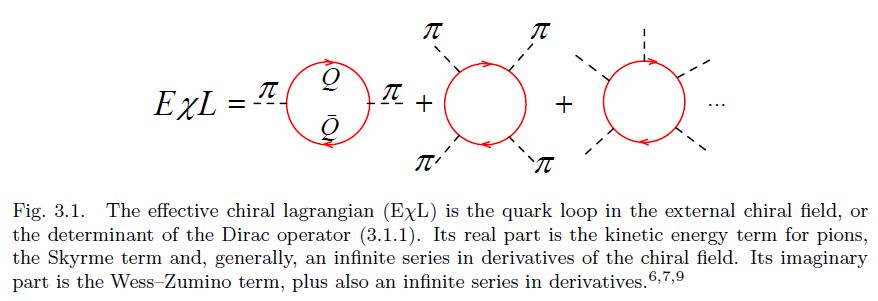
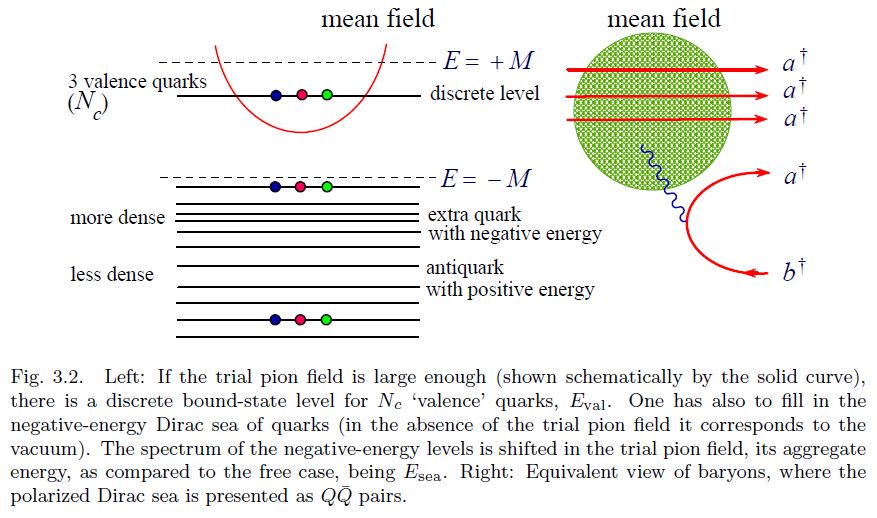
The condition that the winding number of the trial field is unity needs to be imposed to get a deeply bound state, that is to guarantee that the baryon number is unity. 9 The Skyrmion is, thus, nothing but the mean chiral field binding quarks in a baryon.
-
Dmitri Diakonov, Michael I. Eides, Chiral Lagrangian from a functional integral over quarks, JETP Letters 38.7 (1983): 433-436 (pdf, pdf)
-
A. Dhar, Spenta R. Wadia, Nambu—Jona-Lasinio Model: An Effective Lagrangian for Quantum Chromodynamics at Intermediate Length Scales, Phys. Rev. Lett. 52, 959 (1984) (doi:10.1103/PhysRevLett.52.959)
-
Avinash Dhar, R. Shankar, Spenta R. Wadia, Nambu–Jona-Lasinio–type effective Lagrangian: Anomalies and nonlinear Lagrangian of low-energy, large-N QCD, Phys. Rev. D 31, 3256 (1985) (doi:10.1103/PhysRevD.31.3256)
-
Dmitri Diakonov, Victor Petrov, A theory of light quarks in the instanton vacuum, Nuclear Physics B Volume 272, Issue 2, 21 July 1986, Pages 457-489 (doi:10.1016/0550-3213(86)90011-8)
-
Dmitri Diakonov, Victor Petrov, P.V. Pobylitsa, A Chiral Theory of Nucleons, Nucl. Phys. B306 (1988) 809 (spire:247700, doi:10.1016/0550-3213(88)90443-9)
Chapter 4
On Skyrmions with heavy mesons:
- Norberto Scoccola, Heavy quark skyrmions, (arXiv:0905.2722, doi:10.1142/9789814280709_0004), Chapter 4 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Chapter 5
On the Skyrmion model in thermal QFT, with emphasis on the omega-meson/baryon current-coupling:
- Byung-Yoon Park, Vicente Vento, Skyrmion approach to finite density and temperature (arXiv:0906.3263, doi:10.1142/9789814280709_0005), Chapter 5 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Chapter 6
On mesons as gauge bosons of a hidden local symmetry and then as KK-modes of a 5-dimensional holographic Yang-Mills theory:
- Hyun Kyu Lee, Mannque Rho, Half-Skyrmion Hadronic Matter at High Density (doi:10.1142/9789814280709_0006), Chapter 6 in: Mannque Rho et al., The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Condensed matter
On Skyrmions in condensed matter physics:
(…)
String theory
On the skyrmion model for baryons appearing within the Sakai-Sugimoto model of holographic quantum chromodynamics in string theory, as the boundary field theory of D=5 super Yang-Mills theory:
Chapter 15
- Shigeki Sugimoto, Skyrmions and String theory
Chapter 16
- Piljin Yi, Holographic Baryons (arXiv:0902.4515, doi:10.1142/9789814280709_0016), Chapter 16 in: Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
QCD is a challenging theory. Its most interesting aspects, namely the confinement of color and the chiral symmetry breaking, have defied all analytical approaches. While there are now many data accumulated from the lattice gauge theory, the methodology falls well short of giving us insights on how one may understand these phenomena analytically, nor does it give us a systematic way of obtaining a low energy theory of QCD below the confinement scale.
it has been proposed early on that baryons are topological solitons, namely Skyrmions but the usual Skyrmion picture of the baryon has to be modified significantly in the context of full QCD. the holographic picture naturally brings a gauge principle in the bulk description of the flavor dynamics in such a way that all spin one mesons as well as pions would enter the skyrmionic-construction of baryons on the equal footing.
holographic QCD is similar to the chiral perturbation theory in the sense that we deal with exclusively gauge-invariant operators of the theory. The huge difference is, however, that this new approach tends to treat all gauge-invariant objects together. Not only the light meson fields like pions but also heavy vector mesons and baryons appear together, at least in principle. In other words, a holographic QCD deals with all color-singlets simultaneously, giving us a lot more predictive power.
The expectation that there exists a more intelligent theory consisting only of gauge-invariant objects in the large Nc limit is thus realized via string theory in a somewhat surprising manner that the master fields, those truly physical degrees of freedom, actually live not in four dimensional Minkowskian world but in five or higher dimensional curved geometry. This is not however completely unanticipated, and was heralded in the celebrated work by Eguchi and Kawai in early 1980’s which is all the more remarkable in retrospect.
To compare against actual QCD, we must fix the 't Hooft coupling and the KK-scale to fit both the pion decay constant and the mass of the first vector meson. After this fitting, all other infinite number of masses and coupling constants are fixed. This version the holographic WSS model of the holographic QCD is extremely predictive.
this elevates the classic Skyrme picture based on pions to a unified model involving all spin one mesons in addition to pions. This is why the picture is extremely predictive.
As we saw in this note, for low momentum processes, such as soft pion processes, soft rho meson exchanges, and soft elastic scattering of photons, the holographic WSS-model’s predictions compare extremely well with experimental data. It is somewhat mysterious that the baryon sector works out almost as well as the meson sector
Chapter 17
On deriving the Cheshire cat principle of the quark bag model from AdS/QCD:
- Holger Bech Nielsen, Ismail Zahed, The Cheshire Cat Principle from Holography (doi:10.1142/9789814280709_0017, arXiv:0904.0429), Chapter 17 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Chapter 18
On deriving baryon-masses from holographic QCD:
- Alex Pomarol, Andrea Wulzer, Baryon physics in a five-dimensional model of hadrons (arXiv:0904.2272), Chapter 18 in: Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
(…)
Last revised on August 13, 2021 at 20:24:02. See the history of this page for a list of all contributions to it.