nLab skyrmion
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Topological physics
Topological Physics – Phenomena in physics controlled by the topology (often: the homotopy theory) of the physical system.
General theory:
In metamaterials:
For quantum computation:
Contents
- Idea
- Definition
- Properties
- Relation to chiral perturbation theory
- As a model for atomic nuclei
- As a holographic boundary theory
- As the ultimate bag model
- Related concepts
- History
- References
- General
- Skyrmions from rational maps
- Skyrme hadrodynamics with vector mesons (---model)
- Inclusion of the -meson
- Inclusion of the -meson
- Inclusion of the - and -meson
- Inclusion of the -meson
- Skyrme hadrodynamics with heavy quarks/mesons
- Inclusion of strange quarks/kaons
- Inclusion of charm quarks/D-mesons
- Inclusion of bottom quarks/B-mesons
- The WZW term of QCD chiral perturbation theory
- General
- Including light vector mesons
- Including heavy scalar mesons
- Including heavy vector mesons
- Including electroweak interactions
- Hadrons as KK-modes of 5d Yang-Mills theory
- As a model for atomic nculei
- As a models for neutron star
- Relation to instantons, calorons, solitons, monopoles
- In solid state physics
Idea
Skyrme had studied with attention Kelvin's ideas on vortex atoms.
A Skyrmion is a soliton in certain (flavour) gauge field theories. The concept exists quite generally (see Rho-Zahed 16), but its original use (Skyrme 62), and still the most important one, realizes baryons and atomic nuclei as solitons in the light meson-fields of chiral perturbation theory, thus serving as a putative theory of non-perturbative quantum chromodynamics, the formulation of the latter being by and large an open problem (due to confinement, see mass gap problem).

graphics grabbed from Manton 11
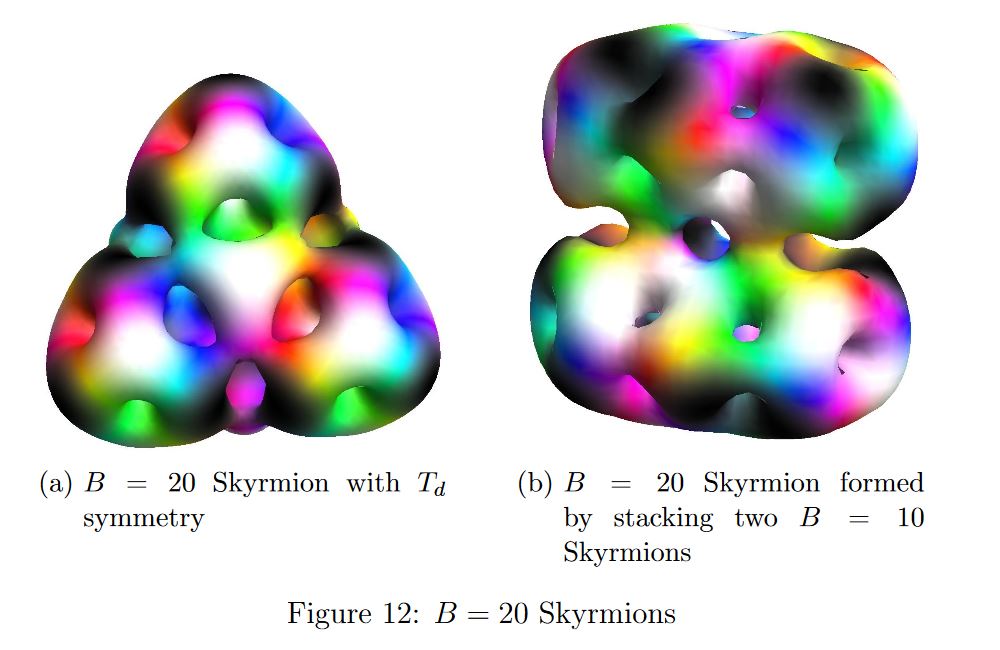
graphics grabbed form FLM 12
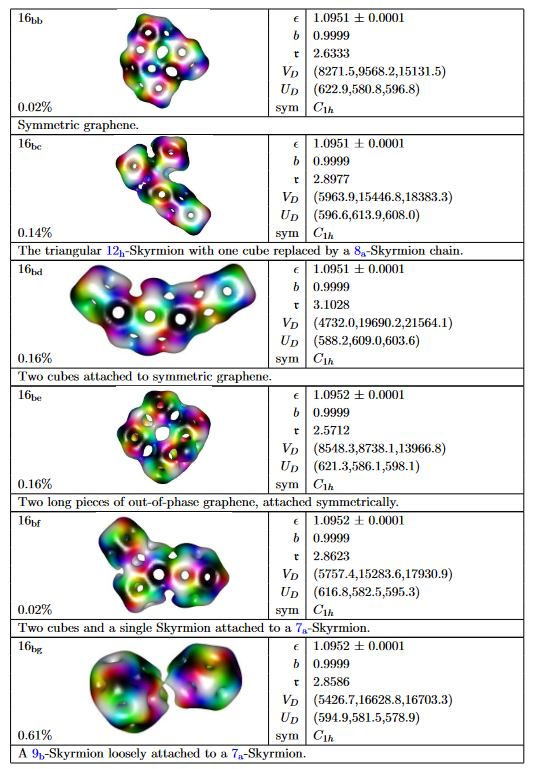
graphics grabbed from Gudnason & Halcrow 2022
Definition
For a simple Lie group with semisimple Lie algebra denoted , with Lie bracket and with Killing form , the Skyrme fields are smooth functions
and the Skyrme Lagrangian density is
where is the pullback of the Maurer-Cartan form on , and where denotes the standard Hodge star operator on Euclidean space .
(e.g. Manton 11 (2.2), Cork 18b (1))
A classical Skyrmion is a solution to the corresponding Euler-Lagrange equations which
-
extremizes the energy implied by the above Lagrangian.
Properties
Relation to chiral perturbation theory
- Dmitri Diakonov, Victor Petrov, Exotic baryon resonances in the Skyrme model (arXiv:0812.1212, doi:10.1142/9789814704410_0004), Chapter 3 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
It is astounding that Skyrme had suggested his model as early as in 1961 before it has been generally accepted that pions are (pseudo) Goldstone bosons associated with the spontaneous breaking of chiral symmetry, and of course long before Quantum Chromodynamics (QCD) has been put forward as the microscopic theory of strong interactions.
The revival of the Skyrme idea in 1983 is due to Witten who explained the raison d’ˆetre of the Skyrme model from the viewpoint of QCD. In the chiral limit when the light quark masses , , tend to zero, such that the octet of the pseudoscalar mesons π, K , η become nearly massless (pseudo) Goldstone bosons, they are the lightest degrees of freedom of QCD. The effective chiral Lagrangian (EχL) for pseudoscalar mesons, understood as an infinite expansion in the derivatives of the pseudoscalar (or chiral) fields, encodes, in principle, full information about QCD. The famous two-term Skyrme Lagrangian can be understood as a low-energy truncation of this infinite series. Witten has added an important four-derivative Wess–Zumino term to the original Skyrme Lagrangian and pointed out that the overall coefficient in front of the EχL is proportional to the number of quark colours .
Soon after Witten’s work it has been realized that it is possible to bring the Skyrme model and the Skyrmion even closer to QCD and to the more customary language of constituent quarks. It has been first noticed 6, 7a, 7b, 8 that a simple chiral invariant Lagrangian for massive (constituent) quarks interacting with the octet chiral field ,
induces, via a quark loop in the external pseudoscalar fields (see Fig. 3.1), the EχL whose lowest-derivative terms coincide with the Skyrme Lagrangian, including automatically the Wess–Zumino term, with the correct coefficient!
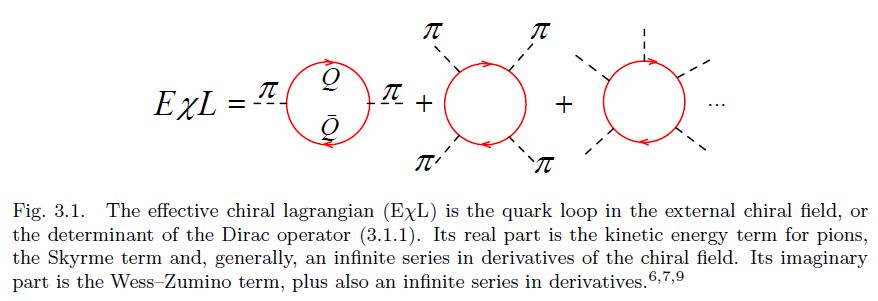
The condition that the winding number of the trial field is unity needs to be imposed to get a deeply bound state, that is to guarantee that the baryon number is unity. 9 The Skyrmion is, thus, nothing but the mean chiral field binding quarks in a baryon.
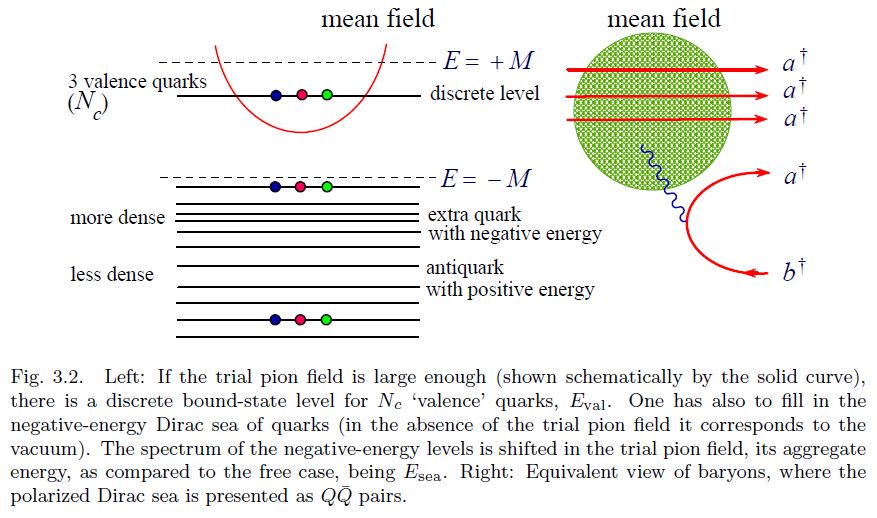
-
Dmitri Diakonov, Michael I. Eides, Chiral Lagrangian from a functional integral over quarks, JETP Letters 38.7 (1983): 433-436 (pdf, pdf)
-
A. Dhar, Spenta R. Wadia, Nambu—Jona-Lasinio Model: An Effective Lagrangian for Quantum Chromodynamics at Intermediate Length Scales, Phys. Rev. Lett. 52, 959 (1984) (doi:10.1103/PhysRevLett.52.959)
-
Avinash Dhar, R. Shankar, Spenta R. Wadia, Nambu–Jona-Lasinio–type effective Lagrangian: Anomalies and nonlinear Lagrangian of low-energy, large-N QCD, Phys. Rev. D 31, 3256 (1985) (doi:10.1103/PhysRevD.31.3256)
-
Dmitri Diakonov, Victor Petrov, A theory of light quarks in the instanton vacuum, Nuclear Physics B Volume 272, Issue 2, 21 July 1986, Pages 457-489 (doi:10.1016/0550-3213(86)90011-8)
-
Dmitri Diakonov, Victor Petrov, P.V. Pobylitsa, A Chiral Theory of Nucleons, Nucl. Phys. B306 (1988) 809 (spire:247700, doi:10.1016/0550-3213(88)90443-9)
As a model for atomic nuclei
Skyrmions are candidate models for baryons and even some aspects of atomic nuclei (Riska 93, Battye-Manton-Sutcliffe 10, Manton 16, Naya-Sutcliffe 18a, Naya-Sutcliffe 18b.
For instance various resonances of the carbon nucleus are modeled well by a Skyrmion with baryon number 12 (Lau-Manton 14):

graphics grabbed form Lau-Manton 14
See also the animated computations in Gudnason & Halcrow 2018.
For Skyrmion models of nuclei to match well to experiment, not just the pion field but also the tower of vector mesons need to be included in the construction.
Including the rho meson gives good results for light nuclei (Naya-Sutcliffe 18a, Naya-Sutcliffe 18b)
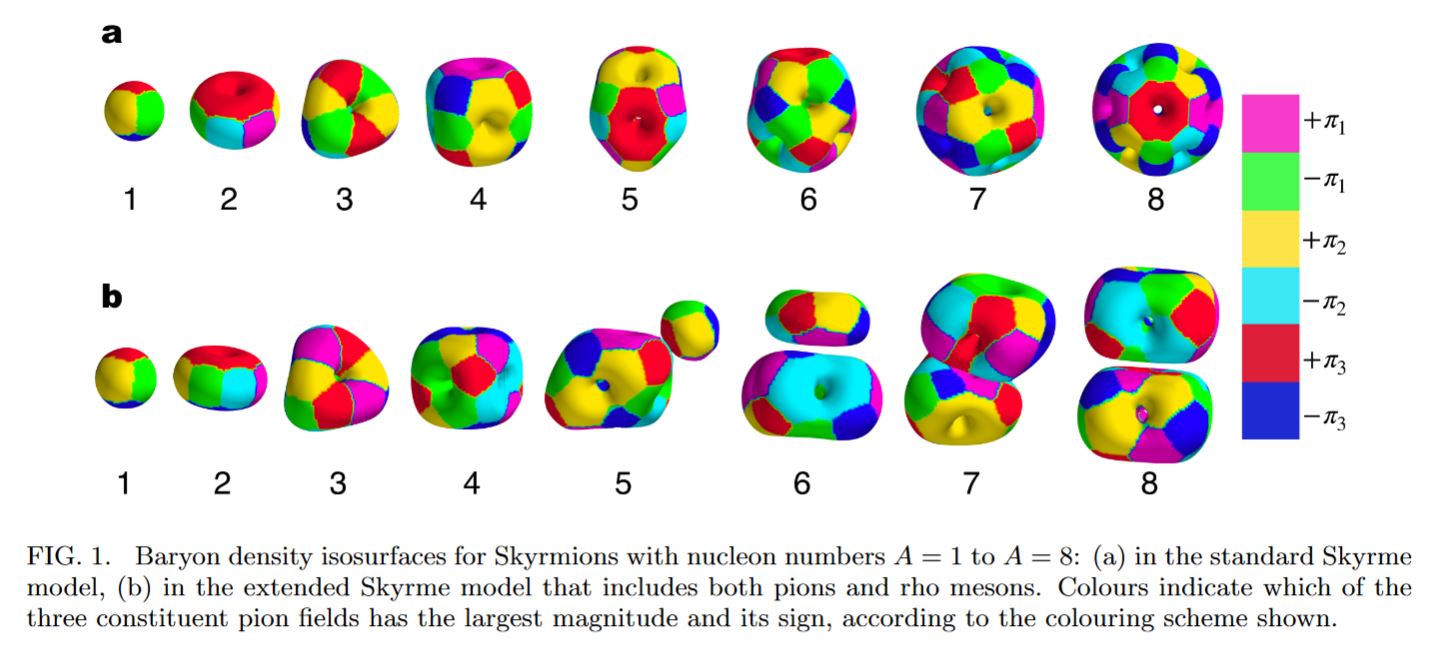
graphics grabbed form Naya-Sutcliffe 18a
An analogous discussion for inclusion of omega-mesons is in Gudnason-Speight 20.
As a holographic boundary theory
The Skyrmions in 4d spacetime above, with vector meson-contributions included, are the holographic/KK-theory reduction of instantons in D=5 Yang-Mills theory (Sakai-Sugimoto 04, Section 5.2, Sakai-Sugimoto 05, Section 3.3, reviewed in Sugimoto 16, Section 15.3.4, Bartolini 17, Section 2.
This phenomenon is essentially the theorem of Atiyah-Manton 89, this is highlighted and developed in Sutcliffe 10, Sutcliffe 15.
In this way Skyrmions (and hence baryons and atomic nuclei, see below) appear in the Witten-Sakai-Sugimoto model, which realizes (something close to) non-perturbative QCD as a D4/D8-intersecting D-brane model described by the AdS-QCD correspondence (“holographic QCD”).
This way, via the equivalence between D4-D8-brane intersections with instantons in the D8-brane-worldvolume, the Skyrme model becomes equivalent to a model of baryons by wrapped D4-branes (Sugimoto 16, 15.4.1):
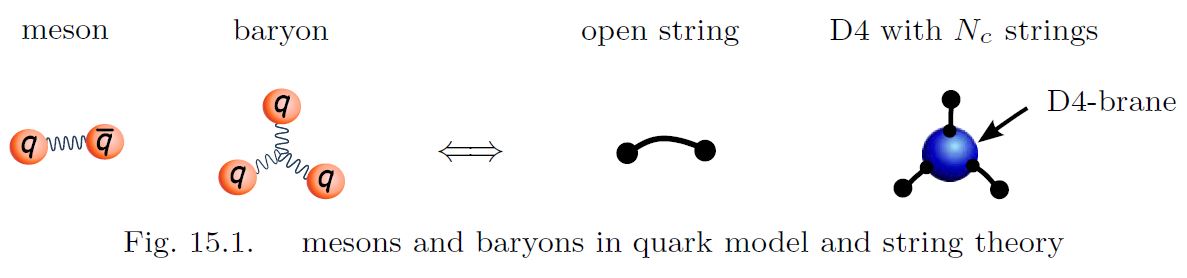
graphics grabbed from Sugimoto 16
As the ultimate bag model
The Skyrmion is the ultimate topological bag model with zero size bag radius, lending further credence to the Cheshire cat principle. (Nielsen-Zahed 09)
Related concepts
effective field theories of nuclear physics, hence for confined-phase quantum chromodynamics:
History
From Rho-Zahed 10, Preface:
Two path-breaking developments took place consecutively in physics in the years 1983 and 1984: First in nuclear physics with the rediscovery of Skyrme’s seminal idea on the structure of baryons and then a “revolution” in string theory in the following year.
at that time the most unconventional idea of Skyrme that fermionic baryons could emerge as topological solitons from π-meson cloud was confirmed in the context of quantum chromodynamics (QCD) in the large number-of-color () limit. It also confirmed how the solitonic structure of baryons, in particular, the nucleons, reconciled nuclear physics — which had been making an impressive progress phenomenologically, aided mostly by experiments — with QCD, the fundamental theory of strong interactions. Immediately after the rediscovery of what is now generically called “skyrmion” came the first string theory revolution which then took most of the principal actors who played the dominant role in reviving the skyrmion picture away from that problem and swept them into the mainstream of string theory reaching out to a much higher energy scale. This was in some sense unfortunate for the skyrmion model per se but fortunate for nuclear physics, for it was then mostly nuclear theorists who picked up what was left behind in the wake of the celebrated string revolution and proceeded to uncover fascinating novel aspects of nuclear structure which otherwise would have eluded physicists, notably concepts such as the ‘Cheshire Cat phenomenon’ in hadronic dynamics.
What has taken place since 1983 is a beautiful story in physics. It has not only profoundly influenced nuclear physics — which was Skyrme’s original aim — but also brought to light hitherto unforseen phenomena in other areas of physics, such as condensed matter physics, astrophysics? and string theory.
References
General
The original articles:
-
Tony Skyrme, A unified field theory of mesons and baryons, Nuclear Physics Volume 31, March–April 1962, Pages 556-569 (doi:10.1016/0029-5582(62)90775-7)
-
Gregory Adkins, Chiara Nappi, Edward Witten, Static Properties of Nucleons in the Skyrme Model, Nucl. Phys. B 228 (1983) 552 [spire:190174, doi:10.1016/0550-3213(83)90559-X]
Monographs:
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific (2016) [doi:10.1142/9710]
-
Nicholas Manton, Skyrmions – A Theory of Nuclei, World Scientific (2022) [doi:10.1142/q0368]
-
Roberto Percacci, section 2.4 of: Non-Perturbative Quantum Field Theory – An Introduction to Topological and Semiclassical Methods, SISSA & ICTP (2024) [doi:10.22323/9788898587056, pdf]
Focus on the underlying topology:
- Aiyalam P. Balachandran, Giuseppe Marmo, Bo-Sture Skagerstam: Classical Topology and Quantum States, World Scientific (1991) [doi:10.1142/1180]
Other review:
- Edward Witten, Skyrmions and QCD, in: Current Algebra and Anomalies, pp. 529-537, World Scientific (1985) (doi:10.1142/9789814503044_0010)
If one assumes confinement, then SU(N)-QCD is equivalent to a theory of mesons (and glueballs) in which the (quartic) meson coupling constant is .
here to stress that QCD is equivalent for any , including , to a meson theory in which is the coupling constant, Large N is special only in that the meson coupling is only moderately weak.
These considerations remove all of the obstacles to interpreting baryons as the solitons of meson physics
There is every evidence that Skyrmions physics with varying couplings reproduces QCD baryons of varying .
The 1/N expansion of QCD, as understood from Feynman diagrams, is the road map which makes the success of Skyrmion physics rationally comprehensible.
-
Eric D'Hoker, Edward Farhi, The Proton as a Topological Twist: A model of elementary particles, without reference to quarks, contains topological structures whose properties match experimental observations remarkably well, American Scientist Vol. 73, No. 6 (November-December 1985), pp. 533-540 (jstor:27853483)
-
Yossef Dothan, L. C. Biedenham, Old models never die: the revival of the Skyrme model, Comments on Nuclear and Particle Physics 17 2 (1987) 63-91 (spire:18567, pdf)
-
Ismail Zahed, Gerald E. Brown The Skyrme model, Physics Reports 142 1–2 (1986) 1-102 [doi:10.1016/0370-1573(86)90142-0]
-
Gerald E. Brown, Mannque Rho, The Chiral Bag, Comments Nucl. Part. Phys. 18 1 (1988) 1-29 [spire:18025]
(in relation to the bag model of quark confinement)
-
Igor Klebanov, Strangeness in the Skyrme model, in: D. Vauthrin, F. Lenz, J. W. Negele, Hadrons and Hadronic Matter, Plenum Press 1989 (doi:10.1007/978-1-4684-1336-6)
(with emphasis on inclusion heavy mesons)
-
Robert E. Marshak, Section 10.5 of: Conceptual Foundations of Modern Particle Physics, World Scientific 1993 (doi:10.1142/1767)
-
Maciej Nowak, Mannque Rho, Ismail Zahed, Chapter 7 of: Chiral Nuclear Dynamics, World Scientific 1996 (doi:10.1142/1681)
-
Herbert Weigel, Baryons as Three Flavor Solitons, Int. J. Mod. Phys. A11:2419-2544, 1996 (arXiv:hep-ph/9509398, cds:288541, doi:10.1142/S0217751X96001218)
-
Ulrich Mosel, Section 17.1 in: Soliton Models of Hadrons (doi:10.1007/978-3-662-03841-3_17), which in turn is Chapter 17 in: Fields, Symmetries, and Quarks, Springer 1999 (doi:10.1007/978-3-662-03841-3)
-
Herbert Weigel, Chiral Soliton Models for Baryons, Lecture Notes in Physics book series, volume 743, Springer 2008 (doi:10.1007/978-3-540-75436-7)
-
Yong-Liang Ma, Masayasu Harada, Lecture notes on the Skyrme model (arXiv:1604.04850, spire:1448311)
-
Nicholas Manton, Skyrmions as Models for Nuclei, Ischia (2022) [pdf]
-
Edward Witten, from 34:05 on in: Some Milestones in the Study of Confinement, talk at Prospects in Theoretical Physics 2023 – Understanding Confinement, IAS (2023) [web, YT]
-
Herbert Weigel: Chiral Solitons [arXiv:2503.20534]
See also
- Wikipedia, Skyrmion
Further development:
-
Nicholas Manton, Classical Skyrmions – Static Solutions and Dynamics, Mathematical Methods in the applied Sciences, Volume35, Issue10, 2012, Pages 1188-1204 (arXiv:1106.1298, doi:10.1002/mma.2512)
-
Atsushi Nakamula, Shin Sasaki, Koki Takesue, Atiyah-Manton Construction of Skyrmions in Eight Dimensions, JHEP 03 (2017) 076 (arXiv:1612.06957)
-
D. T. J. Feist, P. H. C. Lau, Nicholas Manton, Skyrmions up to Baryon Number 108 (arXiv:1210.1712)
-
Nicholas Manton, Lightly Bound Skyrmions, Tetrahedra and Magic Numbers (arXiv:1707.04073)
-
Sven Bjarke Gudnason, Chris Halcrow, Vibrational modes of Skyrmions, Phys. Rev. D 98 125010 (2018) [arXiv:1811.00562, doi:10.1103/PhysRevD.98.125010]
Database of Skyrmion Vibrations [www1.maths.leeds.ac.uk/pure/geometry/SkyrmionVibrations/]
-
Avner Karasik, Skyrmions, Quantum Hall Droplets, and one current to rule them all (arXiv:2003.07893)
-
Carlos Naya, K. Oles, Background fields and self-dual Skyrmions (arXiv:2004.07069)
-
C. Adam, K. Oles, A. Wereszczynski, The Dielectric Skyrme model (arXiv:2005.00018)
-
Sven Bjarke Gudnason, Marco Barsanti, Stefano Bolognesi, Near-BPS baby Skyrmions (arXiv:2006.01726)
-
Sven Bjarke Gudnason, Dielectric Skyrmions (arXiv:2009.03082)
-
Francisco Correa, Andreas Fring, Takanobu Taira, Complex BPS Skyrmions with real energy (arXiv:2102.05781)
-
Chris Halcrow, Thomas Winyard, A consistent two-skyrmion configuration space from instantons (arXiv:2103.15669)
-
Paul Sutcliffe, A Skyrme model with novel chiral symmetry breaking [arXiv:2301.03021]
-
Fabrizio Canfora, Scarlett C. Rebolledo-Caceres, Skyrmions at Finite Density [arXiv:2306.10226]
-
Alberto García Martín-Caro, Chris Halcrow, The charge density and neutron skin thickness of Skyrmions [https://arxiv.org/abs/2312.04335]
-
Sven Bjarke Gudnason, Chris Halcrow, Quantum binding energies in the Skyrme model [arXiv:2307.09272]
-
Josh Cork, Chris Halcrow, Quantisation of skyrmions using instantons [arXiv:2403.17080]
-
Christoph Adam, Alberto Garcia Martin-Caro, Carlos Naya, Andrzej Wereszczynski, Integral identities and universal relations for solitons [arXiv2404.05789]
-
Sven Bjarke Gudnason, Nonlinear rigid-body quantization of Skyrmions [arXiv:2311.11667]
-
Paul Sutcliffe: JNR Skyrmions [arXiv:2409.05058]
-
Josh Cork, Linden Disney-Hogg: Locations of JNR skyrmions [arXiv:2505.00075]
-
L. A. Ferreira, L. R. Livramento: Generalized False Vacuum Skyrme model [arXiv:2506.12235]
Large computer search for Skyrmion solutions:
- Sven Bjarke Gudnason, Chris Halcrow, A Smörgåsbord of Skyrmions [arXiv:2202.01792]
Skyrmion scattering amplitudes:
-
T. Gisiger, M. B. Paranjape, Skyrmion-Skyrmion Scattering (arXiv:hep-th/9310050)
-
David Foster, Steffen Krusch, Scattering of Skyrmions, Nuclear Physics B 897, 697-716, 2015 (arXiv:1412.8719)
-
Chris Halcrow, Derek Harland, An attractive spin-orbit potential from the Skyrme model (arXiv:2007.01304)
-
Derek Harland, Chris Halcrow, Nucleon-nucleon potential from skyrmion dipole interactions (arXiv:2101.02633)
The topic of this paper has a history of mistakes and sign errors in the literature. For both these reasons, we present our calculation in painstaking detail. .
Compared with earlier attempts based on the Skyrme model, we obtain a very good match with the long-range parts of the Paris potential. Overall, these results provide an excellent starting point for describing the nucleon-nucleon interaction from the Skyrme model. Importantly, we can describe many features of the nucleon-nucleon interaction using a purely pionic theory.
our approach could be adapted to any model which treats nuclei as quantised solitons. This includes holographic QCD, where nuclei are described as instantons on a curved spacetime
-
Horatiu Nastase, Jacob Sonnenschein, A -like deformation of the Skyrme model and the Heisenberg model of nucleon-nucleon scattering (arXiv:2101.08232)
(via TT deformation)
Gauged skyrmions with more realistic binding energies (via equivariant de Rham cohomology and maybe some kind of equivariant Hopf degree theorem):
-
Josh Cork, Derek Harland, Thomas Winyard, A model for gauged skyrmions with low binding energies, arXiv:2109.06886]
-
Josh Cork, Derek Harland, Geometry of Gauged Skyrmions, SIGMA 19 o71 (2023) [doi:10.3842/SIGMA.2023.071, arXiv:2303.02623]
-
Nicholas S. Manton: Approach to nuclear cross sections via classical Skyrmion scattering: A proposal [arXiv:2505.12362]
In strong magnetic fields:
- Shi Chen, Zebin Qiu, Kenji Fukushima, Skyrmions in a magnetic field and domain wall formation in dense nuclear matter (arXiv:2104.11482)
Mathematical discussion in differential geometry:
- Christian Gross, Differential Forms on the Skyrmion Bundle, In: Antoine JP., Ali S.T., Lisiecki W., Mladenov I.M., Odzijewicz A. (eds.) Quantization, Coherent States, and Complex Structures, Springer 1995 (doi:10.1007/978-1-4899-1060-8_7)
and in algebraic topology:
- Christian Gross, Topology of the skyrmion bundle, Journal of Mathematical Physics 36, 4406 (1995) (doi:10.1063/1.530899)
Relation to the complex Hopf fibration:
- Sven Bjarke Gudnason, Muneto Nitta, Linking number of vortices as baryon number (arXiv:2002.01762, spire:1778698/)
Generalization to SU(N):
- Pedro D. Alvarez, Sergio L. Cacciatori, Fabrizio Canfora, Bianca Cerchiai, Analytic Skyrmions at finite Baryon density (arXiv:2005.11301)
In higher dimensions:
- Emir Syahreza Fadhilla, Ardian Nata Atmaja, Bobby Eka Gunara, BPS Skyrmions of Generalized Skyrme Model In Higher Dimensions (arXiv:2108.08694)
For the electroweak field:
- Juan Carlos Criado, Valentin V. Khoze, Michael Spannowsky, Electroweak Skyrmions in the HEFT (arXiv:2109.01596)
More in relation to hidden local symmetry:
- Mannque Rho, Skyrmions and Fractional Quantum Hall Droplets Unified by Hidden Symmetries in Dense Matter (arXiv:2109.10059)
Coupling to gravity:
- Vladimir Dzhunushaliev, Vladimir Folomeev, Jutta Kunz, Yakov Shnir: Gravitating Skyrmions with localized fermions [arXiv:2407.17504]
Further resources:
On Skyrmions in relation to chiral effective field theory:
- Nicholas S. Manton, Robustness of the Hedgehog Skyrmion [arXiv:2405.05731]
Skyrmions from rational maps
The following is a list of references on the construction of Skyrmion-solutions of the Yang-Mills field via rational maps from the complex plane, hence holomorphic maps from the Riemann sphere, to itself, akin to the Donaldson-construction of Yang-Mills monopoles.
The original idea:
- Conor J. Houghton, Nicholas Manton, Paul Sutcliffe, Rational Maps, Monopoles and Skyrmions, Nucl. Phys. B510 (1998) 507-537 (arXiv:hep-th/9705151, doi:10.1016/S0550-3213(97)00619-6)
Further discussion:
-
Steffen Krusch, Skyrmions and the Rational Map Ansatz, Nonlinearity 13:2163, 2000 (arXiv:hep-th/0006147)
-
Nicholas S. Manton, Bernard M.A.G. Piette, Understanding Skyrmions using Rational Maps, in: Casacuberta C., Miró-Roig R.M., Verdera J., Xambó-Descamps S. (eds.) European Congress of Mathematics. Progress in Mathematics, vol 201. Birkhäuser, Basel. 2001 (doi:10.1007/978-3-0348-8268-2_27, arXiv:hep-th/0008110)
-
Richard Battye, Paul Sutcliffe, Skyrmions, Fullerenes and Rational Maps, Rev. Math. Phys. 14 (2002) 29-86 (arXiv:hep-th/0103026)
-
W.T. Lin, Bernard M.A.G. Piette, Skyrmion Vibration Modes within the Rational Map Ansatz, Phys. Rev. D77:125028, 2008 (arXiv:0804.4786, doi:10.1103/PhysRevD.77.125028)
-
L. A. Ferreira, L. R. Livramento: Harmonic, Holomorphic and Rational Maps from Self-Duality [arXiv:2412.02636]
On quantization of Skyrmions informed by homotopy of rational maps:
-
Steffen Krusch, Homotopy of rational maps and the quantization of Skyrmions, Annals of Physics Volume 304, Issue 2, April 2003, Pages 103-127 (doi:10.1016/S0003-4916(03)00014-9, arXiv:hep-th/0210310)
-
Steffen Krusch, Skyrmions and Rational Maps, talk at KIAS 2004 (pdf, pdf)
-
Steffen Krusch, Quantization of Skyrmions (arXiv:hep-th/0610176)
the impact of which, on the computation of atomic nuclei, is highlighted in:
- Richard A. Battye, Nicholas Manton, Paul Sutcliffe, p. 23 of: Skyrmions and Nuclei, pp. 3-39 (2010) (doi:10.1142/9789814280709_0001) in: Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
See also:
- Derek Harland, Paul Sutcliffe, Rational Skyrmions arXiv:2307.09355
Skyrme hadrodynamics with vector mesons (---model)
Inclusion of vector mesons (omega-meson and rho-meson/A1-meson) into the Skyrmion model of quantum hadrodynamics, in addition to the pion:
First, on the equivalence between hidden local symmetry- and massive Yang-Mills theory-description of Skyrmion quantum hadrodynamics:
- Atsushi Hosaka, H. Toki, Wolfram Weise, Skyrme Solitons With Vector Mesons: Equivalence of the Massive Yang-Mills and Hidden Local Symmetry Scheme, 1988, Z. Phys. A332 (1989) 97-102 (spire:24079)
See also
- Marcelo Ipinza, Patricio Salgado-Rebolledo, Meron-like topological solitons in massive Yang-Mills theory and the Skyrme model (arXiv:2005.04920)
Inclusion of the -meson
Original proposal for inclusion of the ω-meson in the Skyrme model:
- Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
Relating to nucleon-scattering:
- J. M. Eisenberg, A. Erell, R. R. Silbar, Nucleon-nucleon force in a skyrmion model stabilized by omega exchange, Phys. Rev. C 33, 1531 (1986) (doi:10.1103/PhysRevC.33.1531)
Combination of the omega-meson-stabilized Skyrme model with the bag model for nucleons:
- Atsushi Hosaka, Omega stabilized chiral bag model with a surface coupling, Nuclear Physics A Volume 546, Issue 3, 31 (1992) Pages 493-508 (doi:10.1016/0375-9474(92)90544-T)
Discussion of nucleon phenomenology for the -stabilized Skyrme model:
-
Sven Bjarke Gudnason, James Martin Speight, Realistic classical binding energies in the -Skyrme model (arXiv:2004.12862)
-
Derek Harland, Paul Leask, Martin Speight, Skyrmion crystals stabilized by -mesons [arXiv:2404.11287]
Inclusion of the -meson
Original proposal for inclusion of the ρ-meson:
-
Y. Igarashi, M. Johmura, A. Kobayashi, H. Otsu, T. Sato, S. Sawada, Stabilization of Skyrmions via -Mesons, Nucl.Phys. B259 (1985) 721-729 (spire:213451, doi:10.1016/0550-3213(85)90010-0)
-
Gregory Adkins, Rho mesons in the Skyrme model, Phys. Rev. D 33, 193 (1986) (spire:16895, doi:10.1103/PhysRevD.33.193)
Discussion for phenomenology of light atomic nuclei:
-
Carlos Naya, Paul Sutcliffe, Skyrmions and clustering in light nuclei, Phys. Rev. Lett. 121, 232002 (2018) (arXiv:1811.02064)
-
Carlos Naya, Paul Sutcliffe, Skyrmions in models with pions and rho, JHEP 05 (2018) 174 (arXiv:1803.06098)
APS Synopsis: Revamping the Skyrmion Model, 2018
See also:
- Miguel Huidobro, Paul Leask, Carlos Naya, Andrzej Wereszczynski, Compressibility of dense nuclear matter in the -meson variant of the Skyrme model [arXiv:2405.20757]
Inclusion of the - and -meson
The resulting -- model:
-
Ulf-G. Meissner, Ismail Zahed, Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
(includes also the A1-meson)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, Norbert Kaiser, Andreas Wirzba, Wolfram Weise, Skyrmions with and Mesons as Dynamical Gauge Bosons, Phys. Rev. Lett. 57, 1676 (1986) (doi:10.1103/PhysRevLett.57.1676)
-
Ulf-G. Meissner, Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
L. Zhang, Nimai C. Mukhopadhyay, Baryon physics from mesons: Leading order properties of the nucleon and in the chiral soliton model, Phys. Rev. D 50, 4668 (1994) (doi:10.1103/PhysRevD.50.4668, spire:384906)
-
Yong-Liang Ma, Ghil-Seok Yang, Yongseok Oh, Masayasu Harada, Skyrmions with vector mesons in the hidden local symmetry approach, Phys. Rev. D87:034023, 2013 (arXiv:1209.3554)
-
Ju-Hyun Jung, Ulugbek T. Yakhshiev, Hyun-Chul Kim, In-medium modified -- mesonic Lagrangian and properties of nuclear matter, Physics Letters B Volume 723, Issues 4–5, 25 June 2013, Pages 442-447 (arXiv:1212.4616, doi:10.1016/j.physletb.2013.05.042)
-
Ju-Hyun Jung, Ulugbek Yakhshiev, Hyun-Chul Kim, Peter Schweitzerm, In-medium modified energy-momentum tensor form factors of the nucleon within the framework of a -- soliton model, Phys. Rev. D 89, 114021 (2014) (arXiv:1402.0161)
-
Yongseok Oh, Skyrmions with vector mesons revisited (arXiv:1402.2821)
See also
- Ki-Hoon Hong, Ulugbek Yakhshiev, Hyun-Chul Kim, Modification of hyperon masses in nuclear matter, Phys. Rev. C 99, 035212 (2019) (arXiv:1806.06504)
Review:
-
Roland Kaiser, Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
-
Gottfried Holzwarth, Section 2.3 of: Electromagnetic Form Factors of the Nucleon in Chiral Soliton Models (arXiv:hep-ph/0511194), Chapter 2 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Yongseok Oh, Skyrmions with vector mesons: Single Skyrmion and baryonic matter, 2013 (pdf)
Combination of the omega-rho-Skyrme model with the bag model of quark confinement:
- H. Takashita, S. Yoro, H. Toki, Chiral bag plus skyrmion hybrid model with vector mesons for nucleon, Nuclear Physics A Volume 485, Issues 3–4, August 1988, Pages 589-605 (doi:10.1016/0375-9474(88)90555-6)
Inclusion of the -meson
Inclusion of the sigma-meson:
- Thomas D. Cohen, Explicit meson, topology, and the large- limit of the Skyrmion, Phys. Rev. D 37 (1988) (doi:10.1103/PhysRevD.37.3344)
For analysis of neutron star equation of state:
- David Alvarez-Castillo, Alexander Ayriyan, Gergely Gábor Barnaföldi, Hovik Grigorian, Péter Pósfay, Studying the parameters of the extended - model for neutron star matter (arXiv:2006.03676)
Skyrme hadrodynamics with heavy quarks/mesons
Inclusion of heavy flavors into the Skyrme model for quantum hadrodynamics:
Inclusion of strange quarks/kaons
Inclusion of strange quarks/kaons into the Skyrme model:
-
Curtis Callan, Igor Klebanov, Bound-state approach to strangeness in the Skyrme model, Nuclear Physics B Volume 262, Issue 2, 16 December 1985, Pages 365-382 (doi10.1016/0550-3213(85)90292-5)
-
Curtis Callan, K. Hornbostel, Igor Klebanov, Baryon masses in the bound state approach to strangeness in the skyrme model, Physics Letters B Volume 202, Issue 2, 3 March 1988, Pages 269-275 (doi10.1016/0370-2693(88)90022-6)
-
Norberto Scoccola, D. P. Min, H. Nadeau, Mannque Rho, The strangeness problem: An skyrmion with vector mesons, Nuclear Physics A Volume 505, Issues 3–4, 25 December 1989, Pages 497-524 (doi:10.1016/0375-9474(89)90029-8)
Review:
-
Igor Klebanov, section 6 of: Strangeness in the Skyrme model, in: D. Vauthrin, F. Lenz, J. W. Negele, Hadrons and Hadronic Matter, Plenum Press 1989 (doi:10.1007/978-1-4684-1336-6)
-
Mannque Rho, Section 2.2 of: Cheshire Cat Hadrons, Phys. Rept. 240 (1994) 1-142 (arXiv:hep-ph/9310300, doi:10.1016/0370-1573(94)90002-7)
Inclusion of charm quarks/D-mesons
Inclusion of charm quarks/D-mesons into the Skyrme model:
-
Mannque Rho, D. O. Riska, Norberto Scoccola, Charmed baryons as soliton - D meson bound states, Phys. Lett.B 251 (1990) 597-602 (spire:297771, doi:10.1016/0370-2693(90)90802-D)
-
Yongseok Oh, Dong-Pil Min, Mannque Rho, Norberto Scoccola, Massive-quark baryons as skyrmions: Magnetic moments, Nuclear Physics A Volume 534, Issues 3–4 (1991) Pages 493-512 (doi:10.1016/0375-9474(91)90458-I)
Inclusion of bottom quarks/B-mesons
Inclusion of further heavy flavors beyond strange quark/kaons, namely charm quarks/D-mesons and bottom quarks/B-mesons, into the Skyrme model:
-
Mannque Rho, D. O. Riska, Norberto Scoccola, The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages 343–352 (1992) (doi:10.1007/BF01283544)
-
Arshad Momen, Joseph Schechter, Anand Subbaraman, Heavy Quark Solitons: Strangeness and Symmetry Breaking, Phys. Rev. D49:5970-5978, 1994 (arXiv:hep-ph/9401209)
-
Yongseok Oh, Byung-Yoon Park, Dong-Pil Min, Heavy Baryons as Skyrmion with Corrections, Phys. Rev. D49 (1994) 4649-4658 (arXiv:hep-ph/9402205)
Review:
-
Mannque Rho, Massive-quark baryons as Skyrmions, Modern Physics Letters A, Vol. 06, No. 23 (1991) (doi:10.1142/S0217732391002268)
-
Norberto Scoccola, Heavy quark skyrmions, (arXiv:0905.2722, doi:10.1142/9789814280709_0004), Chapter 4 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
The WZW term of QCD chiral perturbation theory
The gauged WZW term of chiral perturbation theory/quantum hadrodynamics which reproduces the chiral anomaly of QCD in the effective field theory of mesons and Skyrmions:
General
The original articles:
-
Julius Wess, Bruno Zumino, Consequences of anomalous Ward identities, Phys. Lett. B 37 (1971) 95-97 (spire:67330, doi:10.1016/0370-2693(71)90582-X)
-
Edward Witten, Global aspects of current algebra, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 422-432 (doi:10.1016/0550-3213(83)90063-9)
See also:
- O. Kaymakcalan, S. Rajeev, J. Schechter, Nonabelian Anomaly and Vector Meson Decays, Phys. Rev. D 30 (1984) 594 (spire:194756)
Corrections and streamlining of the computations:
-
Chou Kuang-chao, Guo Han-ying, Wu Ke, Song Xing-kang, On the gauge invariance and anomaly-free condition of the Wess-Zumino-Witten effective action, Physics Letters B Volume 134, Issues 1–2, 5 January 1984, Pages 67-69 (doi:10.1016/0370-2693(84)90986-9))
-
H. Kawai, S.-H. H. Tye, Chiral anomalies, effective lagrangians and differential geometry, Physics Letters B Volume 140, Issues 5–6, 14 June 1984, Pages 403-407 (doi:10.1016/0370-2693(84)90780-9)
-
J. L. Mañes, Differential geometric construction of the gauged Wess-Zumino action, Nuclear Physics B Volume 250, Issues 1–4, 1985, Pages 369-384 (doi:10.1016/0550-3213(85)90487-0)
-
Tomáš Brauner, Helena Kolešová, Gauged Wess-Zumino terms for a general coset space, Nuclear Physics B Volume 945, August 2019, 114676 (doi:10.1016/j.nuclphysb.2019.114676)
See also
- Yasunori Lee, Kantaro Ohmori, Yuji Tachikawa, Revisiting Wess-Zumino-Witten terms (arXiv:2009.00033)
Interpretation as Skyrmion/baryon current:
-
Jeffrey Goldstone, Frank Wilczek, Fractional Quantum Numbers on Solitons, Phys. Rev. Lett. 47, 986 (1981) (doi:10.1103/PhysRevLett.47.986)
-
Edward Witten, Current algebra, baryons, and quark confinement, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 433-444 (doi:10.1016/0550-3213(83)90064-0)
-
Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
(beware that the two copies of the text at these two sources differ!)
-
Mannque Rho et al., Introduction, In: Mannque Rho et al. (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Concrete form for -flavor quantum hadrodynamics in 2d:
- C. R. Lee, H. C. Yen, A Derivation of The Wess-Zumino-Witten Action from Chiral Anomaly Using Homotopy Operators, Chinese Journal of Physics, Vol 23 No. 1 (1985) (spire:16389, pdf)
Concrete form for 2 flavors in 4d:
- Masashi Wakamatsu, On the electromagnetic hadron current derived from the gauged Wess-Zumino-Witten action, (arXiv:1108.1236, spire:922302)
Including light vector mesons
Concrete form for 2-flavor quantum hadrodynamics in 4d with light vector mesons included (omega-meson and rho-meson):
-
Ulf-G. Meissner, Ismail Zahed, equation (6) in: Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, equation (2.18) in: Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, equation (2.45) in: Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
Roland Kaiser, equation (12) in: Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
Including heavy scalar mesons
Including heavy scalar mesons:
specifically kaons:
-
Curtis Callan, Igor Klebanov, equation (4.1) in: Bound-state approach to strangeness in the Skyrme model, Nuclear Physics B Volume 262, Issue 2, 16 December 1985, Pages 365-382 (doi10.1016/0550-3213(85)90292-5)
-
Igor Klebanov, equation (99) of: Strangeness in the Skyrme model, in: D. Vauthrin, F. Lenz, J. W. Negele, Hadrons and Hadronic Matter, Plenum Press 1989 (doi:10.1007/978-1-4684-1336-6)
-
N. N. Scoccola, D. P. Min, H. Nadeau, Mannque Rho, equation (2.20) in: The strangeness problem: An skyrmion with vector mesons, Nuclear Physics A Volume 505, Issues 3–4, 25 December 1989, Pages 497-524 (doi:10.1016/0375-9474(89)90029-8)
specifically D-mesons:
(…)
specifically B-mesons:
- Mannque Rho, D. O. Riska, N. N. Scoccola, above (2.1) in: The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages343–352 (1992) (doi:10.1007/BF01283544)
Including heavy vector mesons
Inclusion of heavy vector mesons:
specifically K*-mesons:
- S. Ozaki, H. Nagahiro, Atsushi Hosaka, Equations (3) and (9) in: Magnetic interaction induced by the anomaly in kaon-photoproductions, Physics Letters B Volume 665, Issue 4, 24 July 2008, Pages 178-181 (arXiv:0710.5581, doi:10.1016/j.physletb.2008.06.020)
Including electroweak interactions
Including electroweak fields:
-
J. Bijnens, G. Ecker, A. Picha, The chiral anomaly in non-leptonic weak interactions, Physics Letters B Volume 286, Issues 3–4, 30 July 1992, Pages 341-347 (doi:10.1016/0370-2693(92)91785-8)
-
Gerhard Ecker, Helmut Neufeld, Antonio Pich, Non-leptonic kaon decays and the chiral anomaly, Nuclear Physics B Volume 413, Issues 1–2, 31 January 1994, Pages 321-352 (doi:10.1016/0550-3213(94)90623-8)
Discussion for the full standard model of particle physics:
- Jeffrey Harvey, Christopher T. Hill, Richard J. Hill, Standard Model Gauging of the WZW Term: Anomalies, Global Currents and pseudo-Chern-Simons Interactions, Phys. Rev. D77:085017, 2008 (arXiv:0712.1230)
Hadrons as KK-modes of 5d Yang-Mills theory
The suggestion that the tower of observed vector mesons – when regarded as gauge fields of hidden local symmetries of chiral perturbation theory – is reasonably modeled as a Kaluza-Klein tower of D=5 Yang-Mills theory:
- D. T. Son, M. A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182, doi:10.1103/PhysRevD.69.065020)
That the pure pion-Skyrmion-model of baryons is approximately the KK-reduction of instantons in D=5 Yang-Mills theory is already due to:
- Michael Atiyah, Nicholas Manton, Skyrmions from instantons, Phys. Lett. B, 222(3):438–442, 1989 (doi:10.1016/0370-2693(89)90340-7)
with a hyperbolic space-variant in:
- Michael Atiyah, Paul Sutcliffe, Skyrmions, instantons, mass and curvature, Phys. Lett. B605 (2005) 106-114 (arXiv:hep-th/0411052)
Further discussion of this approximation:
- Josh Cork, Chris Halcrow, ADHM skyrmions (arXiv:2110.15190)
The observation that the result of Atiyah-Manton 89 becomes an exact Kaluza-Klein construction of Skyrmions/baryons from D=5 instantons when the full KK-tower of vector mesons as in Son-Stephanov 03 is included into the Skyrmion model (see also there) is due to:
-
Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
-
Paul Sutcliffe, Holographic Skyrmions, Mod. Phys. Lett. B29 (2015) no. 16, 1540051 (spire:1383608, doi:10.1142/S0217984915400515)
In the Sakai-Sugimoto model of holographic QCD the D=5 Yang-Mills theory of this hadron Kaluza-Klein theory is identified with the worldvolume-theory of D8-flavour branes intersected with D4-branes in an intersecting D-brane model:
-
Tadakatsu Sakai, Shigeki Sugimoto, section 5.2 of Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, section 3.3. of More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)
-
Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, Shinichiro Yamato, Baryons from instantons in holographic QCD, Prog.Theor.Phys.117:1157, 2007 (arXiv:hep-th/0701280)
-
Stefano Bolognesi, Paul Sutcliffe, The Sakai-Sugimoto soliton, JHEP 1401:078, 2014 (arXiv:1309.1396)
-
Lorenzo Bartolini, Stefano Bolognesi, Andrea Proto, From the Sakai-Sugimoto Model to the Generalized Skyrme Model, Phys. Rev. D 97 014024 (2018) [doi:10.1103/PhysRevD.97.014024, arXiv:1711.03873]
-
Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Tommaso Rainaldi, Mass and Isospin Breaking Effects in the Skyrme Model and in Holographic QCD [arXiv:2312.15404]
Extensive review of this holographic/KK-theoretic-realization of quantum hadrodynamics from D=5 Yang-Mills theory is in:
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific, Second edition, 2016 (doi:10.1142/9710)
- Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Via the realization of D4/D8 brane bound states as instantons in the D8-brane worldvolume-theory (see there and there), this relates also to the model of baryons as wrapped D4-branes, originally due to
-
Edward Witten, Baryons And Branes In Anti de Sitter Space, JHEP 9807:006, 1998 (arXiv:hep-th/9805112)
-
David Gross, Hirosi Ooguri, Aspects of Large Gauge Theory Dynamics as Seen by String Theory, Phys. Rev. D58:106002, 1998 (arXiv:hep-th/9805129)
and further developed in the nuclear matrix model:
-
Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
In relation to Yang-Mills monopoles:
- Stefano Bolognesi, Solitons, Large and Holography, 2015 (pdf)
Discussion, in this context, of D-term effects affecting hadron stability:
- Mitsutoshi Fujita, Yoshitaka Hatta, Shigeki Sugimoto, Takahiro Ueda, Nucleon D-term in holographic QCD arXiv:2206.06578
More on baryons in the Sakai-Sugimoto model of holographic QCD:
- Salvatore Baldino, Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Holographic Nuclear Physics with Massive Quarks, Phys. Rev. D 103 126015 (2021) [doi:10.1103/PhysRevD.103.126015, arXiv:2102.00680]
More on mesons in holographic QCD:
-
Johanna Erdmenger, Nick Evans, Ingo Kirsch, Ed Threlfall, Mesons in Gauge/Gravity Duals - A Review, Eur. Phys. J. A 35 (2008) 81-133 [arXiv:0711.4467, doi:10.1140/epja/i2007-10540-1]
-
Daniel Ávila, Leonardo Patiño, Melting holographic mesons by cooling a magnetized quark gluon plasma (arXiv:2002.02470)
-
Xuanmin Cao, Hui Liu, Danning Li, Pion quasiparticles and QCD phase transitions at finite temperature and isospin density from holography, Phys. Rev. D 102, 126014 (2020) (arXiv:2009.00289)
-
Xuanmin Cao, Songyu Qiu, Hui Liu, Danning Li, Thermal properties of light mesons from holography (arXiv:2102.10946)
-
Artur Amorim, Miguel S. Costa, Matti Järvinen, Regge theory in a Holographic dual of QCD in the Veneziano Limit (arXiv:2102.11296)
-
Roldão da Rocha, Information in AdS/QCD: mass spectroscopy of isovector mesons, Phys. Rev. D 103 106027 (2021) [arXiv:2103.03924, doi:10.1103/PhysRevD.103.106027]
-
Shahin Mamedov, Narmin Nasibova, Temperature dependence of meson-nucleon coupling constant from the soft-wall model (arXiv:2103.10494)
An alternative scenario of derivation of 4d Skyrmions by KK-compactification of D=5 Yang-Mills theory, now on a closed interval, motivated by M5-branes instead of by D4/D8-brane intersections as in the Sakai-Sugimoto model, is discussed in:
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Skyrme model from 6d theory, Physics Letters B 783 (2018), 222-226 [doi:10.1016/j.physletb.2018.06.052, arXiv:1805.07241]
with related discussion in:
-
Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Non-Abelian sigma models from Yang-Mills theory compactified on a circle, Physics Letters B 781 (2018) 322-326 [doi:10.1016/j.physletb.2018.04.013arXiv:1803.07322]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme-Faddeev model from 5d super-Yang-Mills, Phys. Lett. B 786 (2018) 39-44 [doi:10.1016/j.physletb.2018.09.028, arXiv:1807.11803]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme and Faddeev models in the low-energy limit of 4d Yang-Mills-Higgs theories, Nuclear Physics B 945 (2019) 114675 [doi:10.1016/j.nuclphysb.2019.114675, arXiv:1808.08972]
See also:
- Y. H. Ahn, Sin Kyu Kang, Hyun Min Lee, Towards a Model of Quarks and Leptons (arXiv:2112.13392)
As a model for atomic nculei
Skyrmions modelling atomic nuclei:
-
D. O. Riska, Baryons and nuclei as skyrmions, Czech J Phys (1993) 43: 449 (doi:10.1007/BF01589856)
-
Richard A. Battye, Nicholas Manton, Paul Sutcliffe, Skyrmions and Nuclei, pp. 3-39 (2010) (doi:10.1142/9789814280709_0001) in: Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Nicholas Manton, Skyrmions and Nuclei, talk at Brookhaven National Lab, November 2016 (pdf)
-
Carlos Naya, Paul Sutcliffe, Skyrmions and clustering in light nuclei, Phys. Rev. Lett. 121, 232002 (2018) (arXiv:1811.02064)
-
Carlos Naya, Paul Sutcliffe, Skyrmions in models with pions and rho, JHEP 05 (2018) 174 (arXiv:1803.06098)
APS Synopsis: Revamping the Skyrmion Model, 2018
For carbon:
-
P.H.C. Lau, Nicholas Manton, States of Carbon-12 in the Skyrme Model, Phys. Rev. Lett. 113, 232503 (2014) (arXiv:1408.6680)
-
Christoph Adam, Carlos Naya, Andrzej Wereszczyński, Carbon-12 in the generalized Skyrme model [arXiv:2401.08778]
As a models for neutron star
Discussion of models of neutron stars by Skyrmions:
-
C. Adam, Carlos Naya, J. Sanchez-Guillen, R. Vazquez, A. Wereszczynski, BPS Skyrmions as neutron stars, Physics Letters B Volume 742, 6 March 2015, Pages 136-142 (arXiv:1407.3799)
-
C. Adam, Carlos Naya, J. Sanchez-Guillen, R. Vazquez, A. Wereszczynski, Neutron stars in the BPS Skyrme model: mean-field limit vs. full field theory, Phys. Rev. C 92, 025802 (2015) (arXiv:1503.03095)
-
Xiang-Hai Liu, Yong-Liang Ma, Mannque Rho, Topology change and nuclear symmetry energy in compact-star matter, Phys. Rev. C 99, 055808 (2019) (arXiv:1811.10012)
-
Carlos Naya, Neutron stars within the Skyrme model, Int. J. Mod. Phys. E 28, 1930006 (2019) (arXiv:1910.01145)
-
C. Adam, J. Sanchez-Guillen, R. Vazquez, A. Wereszczynski, Adding crust to BPS Skyrme neutron stars (arXiv:2004.03610)
-
Christoph Adam, Alberto García Martín-Caro, Miguel Huidobro García, Ricardo Vázquez, Andrzej Wereszczynski, A new consistent Neutron Star Equation of State from a Generalized Skyrme model (arXiv:2006.07983)
-
Christoph Adam, Alberto García Martín-Caro, Miguel Huidobro, Ricardo Vázquez, Andrzej Wereszczynski, Quasi-universal relations for generalized Skyrme stars (arXiv:2011.08573)
With higher curvature corrections included (Starobinsky model):
- C. Adam, M. Huidobro, R. Vazquez, A. Wereszczynski, BPS Skyrme neutron s tars in generalized gravity (arXiv:2005.10834)
See also:
-
Mannque Rho, Fractionalized Quasiparticles and the Hadron-Quark Duality in Dense Baryonic Matter (arXiv:2004.09082)
-
Christoph Adam, Alberto García Martín-Caro, Miguel Huidobro, Ricardo Vázquez, Andrzej Wereszczynski, Kaon condensation in skyrmion matter and compact stars [arXiv:2212.00385]
Relation to instantons, calorons, solitons, monopoles
The construction of Skyrmions from instantons is due to
- Michael Atiyah, Nicholas Manton, Skyrmions from instantons, Phys. Lett. B, 222(3):438–442, 1989 (doi:10.1016/0370-2693(89)90340-7)
The relation between skyrmions, instantons, calorons, solitons and monopoles is usefully reviewed and further developed in
-
Josh Cork, Calorons, symmetry, and the soliton trinity, PhD thesis, University of Leeds 2018 (web)
-
Josh Cork, Skyrmions from calorons, J. High Energ. Phys. (2018) 2018: 137 (arXiv:1810.04143)
based on
- Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
which in turn relates to a Minkowski spacetime-version of the holographic realization of Skyrmions in the Sakai-Sugimoto model (AdS/QCD correspondence).
In solid state physics
In solid state physics skyrmions in the magnetization of thin atomic layers are known as magnetic skyrmions.
See also:
- Wikipedia, Magnetic skyrmions
Realizations in experiment and application to computing:
- Andrew Kent et al. Skyrmionics – Computing and memory technologies based on topological excitations in magnets, Journal of Applied Physics 130 (2021) 070908 [arXiv:2101.09947, doi:10.1063/5.0046950]
Review and exposition:
- Andrew Kent, A new spin on magnetism with applications in information processing, talk at CQTS (Nov 2022) [pdf, video]
Last revised on June 17, 2025 at 05:39:43. See the history of this page for a list of all contributions to it.