nLab meson
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
- Idea
- Examples
- Properties
- Related concepts
- References
- General
- In chiral perturbation theory
- Walecka hadrodynamics with nucleon fields
- Hadrodynamics via Light-front QCD
- Skyrme hadrodynamics with vector mesons (---model)
- Inclusion of the -meson
- Inclusion of the -meson
- Inclusion of the - and -meson
- Inclusion of the -meson
- Skyrme hadrodynamics with heavy quarks/mesons
- Inclusion of strange quarks/kaons
- Inclusion of charm quarks/D-mesons
- Inclusion of bottom quarks/B-mesons
- The WZW term of QCD chiral perturbation theory
- General
- Including light vector mesons
- Including heavy scalar mesons
- Including heavy vector mesons
- Including electroweak interactions
- Hadrons as KK-modes of 5d Yang-Mills theory
- In the large limit
Idea
In QCD a meson is a bound state of two quarks via the strong nuclear force.
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
Examples
First-generation mesons
The mesons in the first generation of fermions, being bound states of up quarks and down quarks are
As linear representations of the Lorentz group (or rather of thePin group) and isospin flavour group (under Wigner classification) these first-generation meson fields are given as in the first of the following two tables:
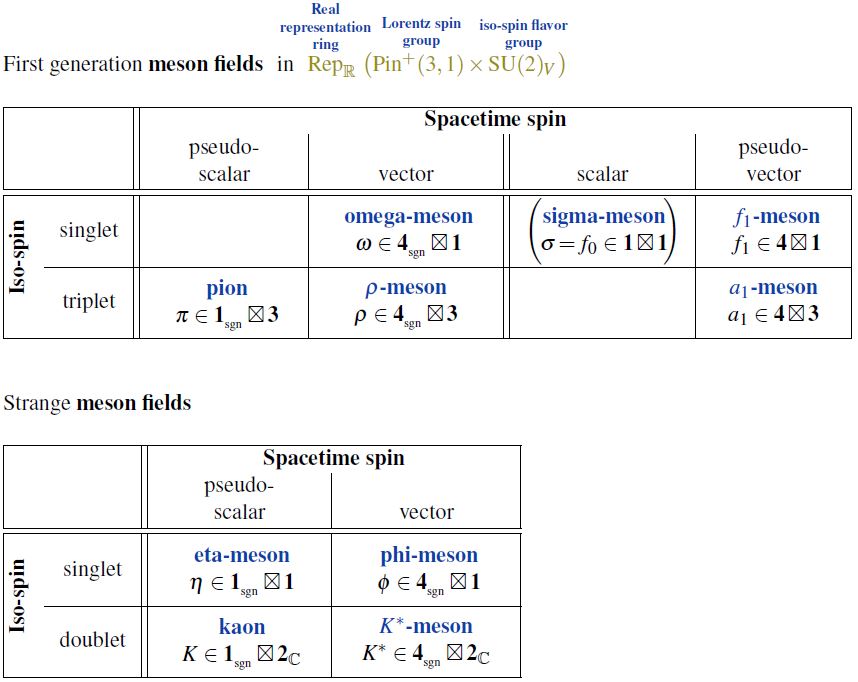
Here denotes an irreducible representation of dimension , and the subscript indicates the one of the two irreps of that dimension which pick up an extra sign under orientation-reversal ( for the sign representation).
So the pion is a Lorentz-pseudoscalar, and the omega-meson and rho-meson are Lorentz pseudovector fields.
As bilinears in the up-quark Weyl spinor field and down-quark Weyl spinor field these meson fields are given as follows (with the Pauli matrices):
Second-generation mesons
Mesons containing strange quarks (the first heavy mesons with respect to 2-flavor chiral perturbation theory) from the second generation of fermions:
Third-generation mesons
Heavy mesons containing bottom quarks from the second generation of fermions:
See also
Properties
Conceptualization and computation in AdS/QCD
In the Witten-Sakai-Sugimoto model for strongly coupled QCD via an intersecting D-brane model, the hadrons in QCD correspond to string-theoretic-phenomena in an ambient bulk field theory on an approximately anti de Sitter spacetime:
-
the mesons (bound states of 2 quarks) correspond to open strings in the bulk, whose two endpoints on the asymptotic boundary correspond to the two quarks;
-
baryons (bound states of quarks) appear in two different but equivalent (Sugimoto 16, 15.4.1) guises:
-
as wrapped D4-branes with open strings connecting them to the D8-brane
-
as skyrmions
(Sakai-Sugimoto 04, section 5.2, Sakai-Sugimoto 05, section 3.3, see Bartolini 17).
-
For review see Sugimoto 16, also Rebhan 14, around (18).
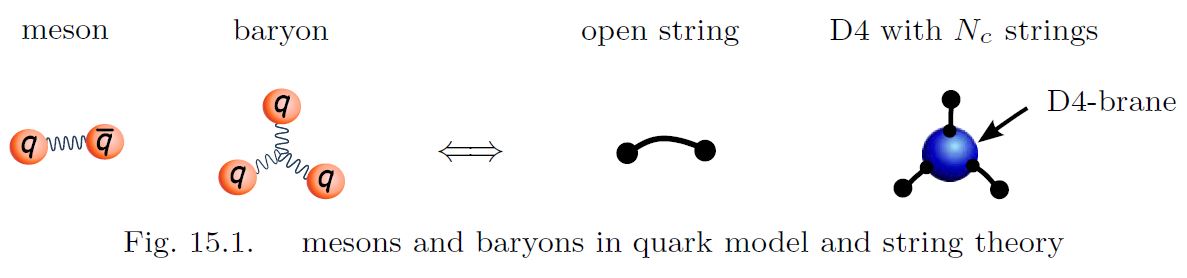
graphics grabbed from Sugimoto 16
This produces baryon mass spectra with moderate quantitative agreement with experiment (HSSY 07):
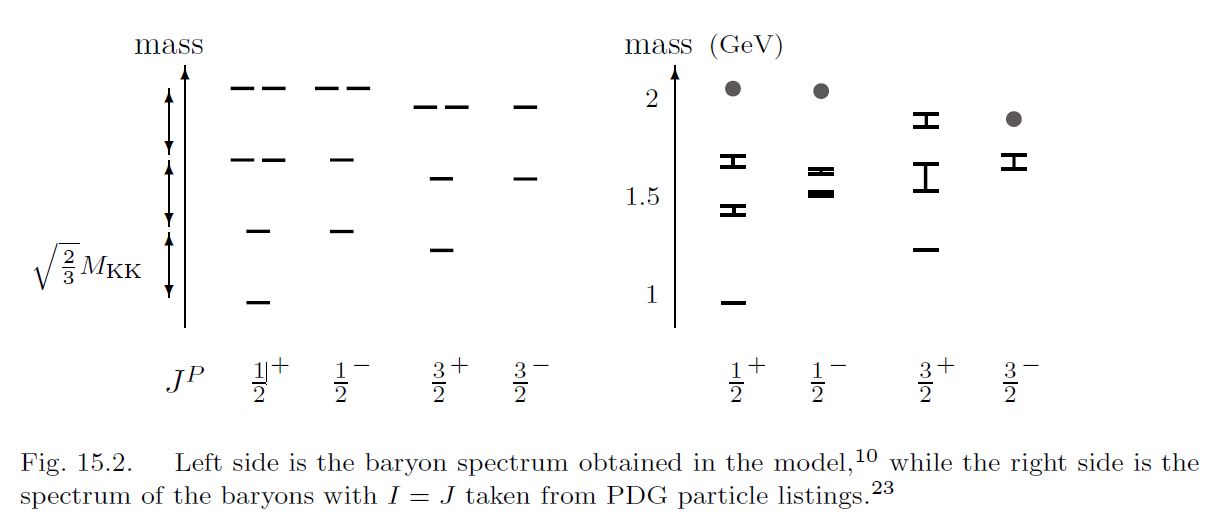
graphics grabbed from Sugimoto 16
Related concepts
References
General
-
Eef van Beveren, George Rupp, Scalar and axial-vector mesons, Eur. Phys. J. A31:468-473, 2007 (arXiv:hep-ph/0610199)
-
Horst Lenske, Igor Strakovsky: Hadron Production Processes [arXiv:2507.21144]
Origin of effective field theory of mesons in nuclear physics, via hidden local gauge symmetry:
- Jun John Sakurai, Theory of strong interactions, Annals Phys. 11 (1960) 1-48 (spire:3218, doi:10.1016/0003-4916(60)90126-3)
Introduction and survey:
-
Jun John Sakurai, Currents and Mesons, Chicago Lectures in Physics, based on notes by George Barry, University of Chicago Press (1969) (ISBN: 9780226733838)
-
Rupert Machleidt, The Meson Theory of Nuclear Forces and Nuclear Structure, In: Negele J.W., Vogt E. (eds.) Advances in Nuclear Physics Advances in Nuclear Physics, vol 19. Springer 1989 (doi:10.1007/978-1-4613-9907-0_2)
-
Rupert Machleidt, David Rodríguez Entem, Chiral effective field theory and nuclear forces, Phys. Rept. 503:1-75, 2011 (arXiv:1105.2919, doi:10.1016/j.physrep.2011.02.001)
-
Francesco Giacosa, Conventional mesons below 2 GeV [arXiv:2211.10092]
-
Franz Gross, Eberhard Klempt et al., Section 8 of: 50 Years of Quantum Chromodynamics, EJPC [arXiv:2212.11107]
See also
The pole approximation?:
- Murray Gell-Mann and Fredrik Zachariasen, Form Factors and Vector Mesons, Phys. Rev. 124, 953 (1961) (doi:10.1103/PhysRev.124.953)
In chiral perturbation theory
See the references at chiral perturbation theory.
Walecka hadrodynamics with nucleon fields
On quantum hadrodynamics (relativivist effective field theory of nuclear physics, coupling mesons and nucleons) in the sense of the Walecka model, hence with nucleons appearing as explicit fields (as opposed to being solitonic Skyrmions in the pion field as in chiral perturbation theory).
Precursor:
- Hans-Peter Duerr, Relativistic Effects in Nuclear Forces, Phys. Rev. 103, 469 (1956) (doi:10.1103/PhysRev.103.469)
The original Walecka model (QHD-I model), with nucleons coupled to sigma-mesons and omega-mesons:
- John Dirk Walecka, A Theory of highly condensed matter, Annals Phys. 83 (1974) 491 (spire:91609, dpi:10.1016/0003-4916(74)90208-5)
Inclusion into the Walecka model also of the pion and the rho-meson (the QHD-II model):
-
Brian Serot, A relativistic nuclear field theory with and mesons, Physics Letters B Volume 86, Issue 2, 24 (1979), Pages 146-150 (doi:10.1016/0370-2693(79)90804-9)
-
T Matsui, Brian Serot, The pion propagator in relativistic quantum field theories of the nuclear many-body problem, Annals of Physics Volume 144, Issue 1, November 1982, Pages 107-167 (doi:10.1016/0003-4916(82)90106-3)
Further discussion of these models:
-
S. A. Chin, A relativistic many-body theory of high density matter, Annals of Physics Volume 108, Issue 2, October 1977, Pages 301-367 (doi:10.1016/0003-4916(77)90016-1)
-
Brian Serot, John Dirk Walecka, The Relativistic Nuclear Many Body Problem, Adv. Nucl. Phys. 16 (1986) 1-327 (spire:207866)
-
Brian Serot, Quantum hadrodynamics, Reports on Progress in Physics, Volume 55, Number 11 (1992) (doi:10.1088/0034-4885/55/11/001)
-
Brian Serot, John Dirk Walecka, Chiral QHD with vector mesons, Acta Phys. Polon. B 23 (1992) 655-679 (spire:343513)
-
Maciej Nowak, Mannque Rho, Ismail Zahed, Chiral Nuclear Dynamics, World Scientific 1996 (doi:10.1142/1681)
-
Brian Serot, John Dirk Walecka, Recent Progress in Quantum Hadrodynamics, Int. J. Mod. Phys. E6:515-631, 1997 (arXiv:nucl-th/9701058)
-
R. V. Poberezhnyuk, V. Vovchenko, D. V. Anchishkin, M. I. Gorenstein, Quantum van der Waals and Walecka models of nuclear matter (arXiv:1708.05605)
Further inclusion of electromagnetism (photon field):
- A. Yu. Korchin, D. Van Neck, M. Waroquier, Electromagnetic interaction in chiral quantum hadrodynamics and decay of vector and axial-vector mesons, Phys. Rev. C67 (2003) 015207 (arXiv:nucl-th/0302042)
Relation to quark-meson coupling model:
- Koichi Saito, Relationship between Quark-Meson Coupling Model and Quantum Hadrodynamics, Prog. Theor. Phys. 108 (2002) 609-614 (arXiv:nucl-th/0207053)
Hadrodynamics via Light-front QCD
On light-front QCD for quantum hadrodynamics:
-
International Light Cone Advisory Committee, Light-Front Quantum Chromodynamics: A framework for the analysis of hadron physics, Nuclear Physics B - Proceedings Supplements Volumes 251–252, June–July 2014, Pages 165-174 (arXiv:1309.6333, doi:10.1016/j.nuclphysbps.2014.05.004)
-
Edward Shuryak, Ismail Zahed, Hadronic structure on the light-front I: Instanton effects and quark-antiquark effective potentials (arXiv:2110.15927)
-
Edward Shuryak, Ismail Zahed, Hadronic structure on the light-front II: QCD strings, Wilson lines and potentials (arXiv:2111.01775)
Skyrme hadrodynamics with vector mesons (---model)
Inclusion of vector mesons (omega-meson and rho-meson/A1-meson) into the Skyrmion model of quantum hadrodynamics, in addition to the pion:
First, on the equivalence between hidden local symmetry- and massive Yang-Mills theory-description of Skyrmion quantum hadrodynamics:
- Atsushi Hosaka, H. Toki, Wolfram Weise, Skyrme Solitons With Vector Mesons: Equivalence of the Massive Yang-Mills and Hidden Local Symmetry Scheme, 1988, Z. Phys. A332 (1989) 97-102 (spire:24079)
See also
- Marcelo Ipinza, Patricio Salgado-Rebolledo, Meron-like topological solitons in massive Yang-Mills theory and the Skyrme model (arXiv:2005.04920)
Inclusion of the -meson
Original proposal for inclusion of the ω-meson in the Skyrme model:
- Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
Relating to nucleon-scattering:
- J. M. Eisenberg, A. Erell, R. R. Silbar, Nucleon-nucleon force in a skyrmion model stabilized by omega exchange, Phys. Rev. C 33, 1531 (1986) (doi:10.1103/PhysRevC.33.1531)
Combination of the omega-meson-stabilized Skyrme model with the bag model for nucleons:
- Atsushi Hosaka, Omega stabilized chiral bag model with a surface coupling, Nuclear Physics A Volume 546, Issue 3, 31 (1992) Pages 493-508 (doi:10.1016/0375-9474(92)90544-T)
Discussion of nucleon phenomenology for the -stabilized Skyrme model:
-
Sven Bjarke Gudnason, James Martin Speight, Realistic classical binding energies in the -Skyrme model (arXiv:2004.12862)
-
Derek Harland, Paul Leask, Martin Speight, Skyrmion crystals stabilized by -mesons [arXiv:2404.11287]
Inclusion of the -meson
Original proposal for inclusion of the ρ-meson:
-
Y. Igarashi, M. Johmura, A. Kobayashi, H. Otsu, T. Sato, S. Sawada, Stabilization of Skyrmions via -Mesons, Nucl.Phys. B259 (1985) 721-729 (spire:213451, doi:10.1016/0550-3213(85)90010-0)
-
Gregory Adkins, Rho mesons in the Skyrme model, Phys. Rev. D 33, 193 (1986) (spire:16895, doi:10.1103/PhysRevD.33.193)
Discussion for phenomenology of light atomic nuclei:
-
Carlos Naya, Paul Sutcliffe, Skyrmions and clustering in light nuclei, Phys. Rev. Lett. 121, 232002 (2018) (arXiv:1811.02064)
-
Carlos Naya, Paul Sutcliffe, Skyrmions in models with pions and rho, JHEP 05 (2018) 174 (arXiv:1803.06098)
APS Synopsis: Revamping the Skyrmion Model, 2018
See also:
- Miguel Huidobro, Paul Leask, Carlos Naya, Andrzej Wereszczynski, Compressibility of dense nuclear matter in the -meson variant of the Skyrme model [arXiv:2405.20757]
Inclusion of the - and -meson
The resulting -- model:
-
Ulf-G. Meissner, Ismail Zahed, Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
(includes also the A1-meson)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, Norbert Kaiser, Andreas Wirzba, Wolfram Weise, Skyrmions with and Mesons as Dynamical Gauge Bosons, Phys. Rev. Lett. 57, 1676 (1986) (doi:10.1103/PhysRevLett.57.1676)
-
Ulf-G. Meissner, Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
L. Zhang, Nimai C. Mukhopadhyay, Baryon physics from mesons: Leading order properties of the nucleon and in the chiral soliton model, Phys. Rev. D 50, 4668 (1994) (doi:10.1103/PhysRevD.50.4668, spire:384906)
-
Yong-Liang Ma, Ghil-Seok Yang, Yongseok Oh, Masayasu Harada, Skyrmions with vector mesons in the hidden local symmetry approach, Phys. Rev. D87:034023, 2013 (arXiv:1209.3554)
-
Ju-Hyun Jung, Ulugbek T. Yakhshiev, Hyun-Chul Kim, In-medium modified -- mesonic Lagrangian and properties of nuclear matter, Physics Letters B Volume 723, Issues 4–5, 25 June 2013, Pages 442-447 (arXiv:1212.4616, doi:10.1016/j.physletb.2013.05.042)
-
Ju-Hyun Jung, Ulugbek Yakhshiev, Hyun-Chul Kim, Peter Schweitzerm, In-medium modified energy-momentum tensor form factors of the nucleon within the framework of a -- soliton model, Phys. Rev. D 89, 114021 (2014) (arXiv:1402.0161)
-
Yongseok Oh, Skyrmions with vector mesons revisited (arXiv:1402.2821)
See also
- Ki-Hoon Hong, Ulugbek Yakhshiev, Hyun-Chul Kim, Modification of hyperon masses in nuclear matter, Phys. Rev. C 99, 035212 (2019) (arXiv:1806.06504)
Review:
-
Roland Kaiser, Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
-
Gottfried Holzwarth, Section 2.3 of: Electromagnetic Form Factors of the Nucleon in Chiral Soliton Models (arXiv:hep-ph/0511194), Chapter 2 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Yongseok Oh, Skyrmions with vector mesons: Single Skyrmion and baryonic matter, 2013 (pdf)
Combination of the omega-rho-Skyrme model with the bag model of quark confinement:
- H. Takashita, S. Yoro, H. Toki, Chiral bag plus skyrmion hybrid model with vector mesons for nucleon, Nuclear Physics A Volume 485, Issues 3–4, August 1988, Pages 589-605 (doi:10.1016/0375-9474(88)90555-6)
Inclusion of the -meson
Inclusion of the sigma-meson:
- Thomas D. Cohen, Explicit meson, topology, and the large- limit of the Skyrmion, Phys. Rev. D 37 (1988) (doi:10.1103/PhysRevD.37.3344)
For analysis of neutron star equation of state:
- David Alvarez-Castillo, Alexander Ayriyan, Gergely Gábor Barnaföldi, Hovik Grigorian, Péter Pósfay, Studying the parameters of the extended - model for neutron star matter (arXiv:2006.03676)
Skyrme hadrodynamics with heavy quarks/mesons
Inclusion of heavy flavors into the Skyrme model for quantum hadrodynamics:
Inclusion of strange quarks/kaons
Inclusion of strange quarks/kaons into the Skyrme model:
-
Curtis Callan, Igor Klebanov, Bound-state approach to strangeness in the Skyrme model, Nuclear Physics B Volume 262, Issue 2, 16 December 1985, Pages 365-382 (doi10.1016/0550-3213(85)90292-5)
-
Curtis Callan, K. Hornbostel, Igor Klebanov, Baryon masses in the bound state approach to strangeness in the skyrme model, Physics Letters B Volume 202, Issue 2, 3 March 1988, Pages 269-275 (doi10.1016/0370-2693(88)90022-6)
-
Norberto Scoccola, D. P. Min, H. Nadeau, Mannque Rho, The strangeness problem: An skyrmion with vector mesons, Nuclear Physics A Volume 505, Issues 3–4, 25 December 1989, Pages 497-524 (doi:10.1016/0375-9474(89)90029-8)
Review:
-
Igor Klebanov, section 6 of: Strangeness in the Skyrme model, in: D. Vauthrin, F. Lenz, J. W. Negele, Hadrons and Hadronic Matter, Plenum Press 1989 (doi:10.1007/978-1-4684-1336-6)
-
Mannque Rho, Section 2.2 of: Cheshire Cat Hadrons, Phys. Rept. 240 (1994) 1-142 (arXiv:hep-ph/9310300, doi:10.1016/0370-1573(94)90002-7)
Inclusion of charm quarks/D-mesons
Inclusion of charm quarks/D-mesons into the Skyrme model:
-
Mannque Rho, D. O. Riska, Norberto Scoccola, Charmed baryons as soliton - D meson bound states, Phys. Lett.B 251 (1990) 597-602 (spire:297771, doi:10.1016/0370-2693(90)90802-D)
-
Yongseok Oh, Dong-Pil Min, Mannque Rho, Norberto Scoccola, Massive-quark baryons as skyrmions: Magnetic moments, Nuclear Physics A Volume 534, Issues 3–4 (1991) Pages 493-512 (doi:10.1016/0375-9474(91)90458-I)
Inclusion of bottom quarks/B-mesons
Inclusion of further heavy flavors beyond strange quark/kaons, namely charm quarks/D-mesons and bottom quarks/B-mesons, into the Skyrme model:
-
Mannque Rho, D. O. Riska, Norberto Scoccola, The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages 343–352 (1992) (doi:10.1007/BF01283544)
-
Arshad Momen, Joseph Schechter, Anand Subbaraman, Heavy Quark Solitons: Strangeness and Symmetry Breaking, Phys. Rev. D49:5970-5978, 1994 (arXiv:hep-ph/9401209)
-
Yongseok Oh, Byung-Yoon Park, Dong-Pil Min, Heavy Baryons as Skyrmion with Corrections, Phys. Rev. D49 (1994) 4649-4658 (arXiv:hep-ph/9402205)
Review:
-
Mannque Rho, Massive-quark baryons as Skyrmions, Modern Physics Letters A, Vol. 06, No. 23 (1991) (doi:10.1142/S0217732391002268)
-
Norberto Scoccola, Heavy quark skyrmions, (arXiv:0905.2722, doi:10.1142/9789814280709_0004), Chapter 4 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
The WZW term of QCD chiral perturbation theory
The gauged WZW term of chiral perturbation theory/quantum hadrodynamics which reproduces the chiral anomaly of QCD in the effective field theory of mesons and Skyrmions:
General
The original articles:
-
Julius Wess, Bruno Zumino, Consequences of anomalous Ward identities, Phys. Lett. B 37 (1971) 95-97 (spire:67330, doi:10.1016/0370-2693(71)90582-X)
-
Edward Witten, Global aspects of current algebra, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 422-432 (doi:10.1016/0550-3213(83)90063-9)
See also:
- O. Kaymakcalan, S. Rajeev, J. Schechter, Nonabelian Anomaly and Vector Meson Decays, Phys. Rev. D 30 (1984) 594 (spire:194756)
Corrections and streamlining of the computations:
-
Chou Kuang-chao, Guo Han-ying, Wu Ke, Song Xing-kang, On the gauge invariance and anomaly-free condition of the Wess-Zumino-Witten effective action, Physics Letters B Volume 134, Issues 1–2, 5 January 1984, Pages 67-69 (doi:10.1016/0370-2693(84)90986-9))
-
H. Kawai, S.-H. H. Tye, Chiral anomalies, effective lagrangians and differential geometry, Physics Letters B Volume 140, Issues 5–6, 14 June 1984, Pages 403-407 (doi:10.1016/0370-2693(84)90780-9)
-
J. L. Mañes, Differential geometric construction of the gauged Wess-Zumino action, Nuclear Physics B Volume 250, Issues 1–4, 1985, Pages 369-384 (doi:10.1016/0550-3213(85)90487-0)
-
Tomáš Brauner, Helena Kolešová, Gauged Wess-Zumino terms for a general coset space, Nuclear Physics B Volume 945, August 2019, 114676 (doi:10.1016/j.nuclphysb.2019.114676)
See also
- Yasunori Lee, Kantaro Ohmori, Yuji Tachikawa, Revisiting Wess-Zumino-Witten terms (arXiv:2009.00033)
Interpretation as Skyrmion/baryon current:
-
Jeffrey Goldstone, Frank Wilczek, Fractional Quantum Numbers on Solitons, Phys. Rev. Lett. 47, 986 (1981) (doi:10.1103/PhysRevLett.47.986)
-
Edward Witten, Current algebra, baryons, and quark confinement, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 433-444 (doi:10.1016/0550-3213(83)90064-0)
-
Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
(beware that the two copies of the text at these two sources differ!)
-
Mannque Rho et al., Introduction, In: Mannque Rho et al. (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Concrete form for -flavor quantum hadrodynamics in 2d:
- C. R. Lee, H. C. Yen, A Derivation of The Wess-Zumino-Witten Action from Chiral Anomaly Using Homotopy Operators, Chinese Journal of Physics, Vol 23 No. 1 (1985) (spire:16389, pdf)
Concrete form for 2 flavors in 4d:
- Masashi Wakamatsu, On the electromagnetic hadron current derived from the gauged Wess-Zumino-Witten action, (arXiv:1108.1236, spire:922302)
Including light vector mesons
Concrete form for 2-flavor quantum hadrodynamics in 4d with light vector mesons included (omega-meson and rho-meson):
-
Ulf-G. Meissner, Ismail Zahed, equation (6) in: Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, equation (2.18) in: Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, equation (2.45) in: Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
Roland Kaiser, equation (12) in: Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
Including heavy scalar mesons
Including heavy scalar mesons:
specifically kaons:
-
Curtis Callan, Igor Klebanov, equation (4.1) in: Bound-state approach to strangeness in the Skyrme model, Nuclear Physics B Volume 262, Issue 2, 16 December 1985, Pages 365-382 (doi10.1016/0550-3213(85)90292-5)
-
Igor Klebanov, equation (99) of: Strangeness in the Skyrme model, in: D. Vauthrin, F. Lenz, J. W. Negele, Hadrons and Hadronic Matter, Plenum Press 1989 (doi:10.1007/978-1-4684-1336-6)
-
N. N. Scoccola, D. P. Min, H. Nadeau, Mannque Rho, equation (2.20) in: The strangeness problem: An skyrmion with vector mesons, Nuclear Physics A Volume 505, Issues 3–4, 25 December 1989, Pages 497-524 (doi:10.1016/0375-9474(89)90029-8)
specifically D-mesons:
(…)
specifically B-mesons:
- Mannque Rho, D. O. Riska, N. N. Scoccola, above (2.1) in: The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages343–352 (1992) (doi:10.1007/BF01283544)
Including heavy vector mesons
Inclusion of heavy vector mesons:
specifically K*-mesons:
- S. Ozaki, H. Nagahiro, Atsushi Hosaka, Equations (3) and (9) in: Magnetic interaction induced by the anomaly in kaon-photoproductions, Physics Letters B Volume 665, Issue 4, 24 July 2008, Pages 178-181 (arXiv:0710.5581, doi:10.1016/j.physletb.2008.06.020)
Including electroweak interactions
Including electroweak fields:
-
J. Bijnens, G. Ecker, A. Picha, The chiral anomaly in non-leptonic weak interactions, Physics Letters B Volume 286, Issues 3–4, 30 July 1992, Pages 341-347 (doi:10.1016/0370-2693(92)91785-8)
-
Gerhard Ecker, Helmut Neufeld, Antonio Pich, Non-leptonic kaon decays and the chiral anomaly, Nuclear Physics B Volume 413, Issues 1–2, 31 January 1994, Pages 321-352 (doi:10.1016/0550-3213(94)90623-8)
Discussion for the full standard model of particle physics:
- Jeffrey Harvey, Christopher T. Hill, Richard J. Hill, Standard Model Gauging of the WZW Term: Anomalies, Global Currents and pseudo-Chern-Simons Interactions, Phys. Rev. D77:085017, 2008 (arXiv:0712.1230)
Hadrons as KK-modes of 5d Yang-Mills theory
The suggestion that the tower of observed vector mesons – when regarded as gauge fields of hidden local symmetries of chiral perturbation theory – is reasonably modeled as a Kaluza-Klein tower of D=5 Yang-Mills theory:
- D. T. Son, M. A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182, doi:10.1103/PhysRevD.69.065020)
That the pure pion-Skyrmion-model of baryons is approximately the KK-reduction of instantons in D=5 Yang-Mills theory is already due to:
- Michael Atiyah, Nicholas Manton, Skyrmions from instantons, Phys. Lett. B, 222(3):438–442, 1989 (doi:10.1016/0370-2693(89)90340-7)
with a hyperbolic space-variant in:
- Michael Atiyah, Paul Sutcliffe, Skyrmions, instantons, mass and curvature, Phys. Lett. B605 (2005) 106-114 (arXiv:hep-th/0411052)
Further discussion of this approximation:
- Josh Cork, Chris Halcrow, ADHM skyrmions (arXiv:2110.15190)
The observation that the result of Atiyah-Manton 89 becomes an exact Kaluza-Klein construction of Skyrmions/baryons from D=5 instantons when the full KK-tower of vector mesons as in Son-Stephanov 03 is included into the Skyrmion model (see also there) is due to:
-
Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
-
Paul Sutcliffe, Holographic Skyrmions, Mod. Phys. Lett. B29 (2015) no. 16, 1540051 (spire:1383608, doi:10.1142/S0217984915400515)
In the Sakai-Sugimoto model of holographic QCD the D=5 Yang-Mills theory of this hadron Kaluza-Klein theory is identified with the worldvolume-theory of D8-flavour branes intersected with D4-branes in an intersecting D-brane model:
-
Tadakatsu Sakai, Shigeki Sugimoto, section 5.2 of Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, section 3.3. of More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)
-
Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, Shinichiro Yamato, Baryons from instantons in holographic QCD, Prog.Theor.Phys.117:1157, 2007 (arXiv:hep-th/0701280)
-
Stefano Bolognesi, Paul Sutcliffe, The Sakai-Sugimoto soliton, JHEP 1401:078, 2014 (arXiv:1309.1396)
-
Lorenzo Bartolini, Stefano Bolognesi, Andrea Proto, From the Sakai-Sugimoto Model to the Generalized Skyrme Model, Phys. Rev. D 97 014024 (2018) [doi:10.1103/PhysRevD.97.014024, arXiv:1711.03873]
-
Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Tommaso Rainaldi, Mass and Isospin Breaking Effects in the Skyrme Model and in Holographic QCD [arXiv:2312.15404]
Extensive review of this holographic/KK-theoretic-realization of quantum hadrodynamics from D=5 Yang-Mills theory is in:
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific, Second edition, 2016 (doi:10.1142/9710)
- Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Via the realization of D4/D8 brane bound states as instantons in the D8-brane worldvolume-theory (see there and there), this relates also to the model of baryons as wrapped D4-branes, originally due to
-
Edward Witten, Baryons And Branes In Anti de Sitter Space, JHEP 9807:006, 1998 (arXiv:hep-th/9805112)
-
David Gross, Hirosi Ooguri, Aspects of Large Gauge Theory Dynamics as Seen by String Theory, Phys. Rev. D58:106002, 1998 (arXiv:hep-th/9805129)
and further developed in the nuclear matrix model:
-
Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
In relation to Yang-Mills monopoles:
- Stefano Bolognesi, Solitons, Large and Holography, 2015 (pdf)
Discussion, in this context, of D-term effects affecting hadron stability:
- Mitsutoshi Fujita, Yoshitaka Hatta, Shigeki Sugimoto, Takahiro Ueda, Nucleon D-term in holographic QCD arXiv:2206.06578
More on baryons in the Sakai-Sugimoto model of holographic QCD:
- Salvatore Baldino, Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Holographic Nuclear Physics with Massive Quarks, Phys. Rev. D 103 126015 (2021) [doi:10.1103/PhysRevD.103.126015, arXiv:2102.00680]
More on mesons in holographic QCD:
-
Johanna Erdmenger, Nick Evans, Ingo Kirsch, Ed Threlfall, Mesons in Gauge/Gravity Duals - A Review, Eur. Phys. J. A 35 (2008) 81-133 [arXiv:0711.4467, doi:10.1140/epja/i2007-10540-1]
-
Daniel Ávila, Leonardo Patiño, Melting holographic mesons by cooling a magnetized quark gluon plasma (arXiv:2002.02470)
-
Xuanmin Cao, Hui Liu, Danning Li, Pion quasiparticles and QCD phase transitions at finite temperature and isospin density from holography, Phys. Rev. D 102, 126014 (2020) (arXiv:2009.00289)
-
Xuanmin Cao, Songyu Qiu, Hui Liu, Danning Li, Thermal properties of light mesons from holography (arXiv:2102.10946)
-
Artur Amorim, Miguel S. Costa, Matti Järvinen, Regge theory in a Holographic dual of QCD in the Veneziano Limit (arXiv:2102.11296)
-
Roldão da Rocha, Information in AdS/QCD: mass spectroscopy of isovector mesons, Phys. Rev. D 103 106027 (2021) [arXiv:2103.03924, doi:10.1103/PhysRevD.103.106027]
-
Shahin Mamedov, Narmin Nasibova, Temperature dependence of meson-nucleon coupling constant from the soft-wall model (arXiv:2103.10494)
An alternative scenario of derivation of 4d Skyrmions by KK-compactification of D=5 Yang-Mills theory, now on a closed interval, motivated by M5-branes instead of by D4/D8-brane intersections as in the Sakai-Sugimoto model, is discussed in:
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Skyrme model from 6d theory, Physics Letters B 783 (2018), 222-226 [doi:10.1016/j.physletb.2018.06.052, arXiv:1805.07241]
with related discussion in:
-
Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Non-Abelian sigma models from Yang-Mills theory compactified on a circle, Physics Letters B 781 (2018) 322-326 [doi:10.1016/j.physletb.2018.04.013arXiv:1803.07322]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme-Faddeev model from 5d super-Yang-Mills, Phys. Lett. B 786 (2018) 39-44 [doi:10.1016/j.physletb.2018.09.028, arXiv:1807.11803]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme and Faddeev models in the low-energy limit of 4d Yang-Mills-Higgs theories, Nuclear Physics B 945 (2019) 114675 [doi:10.1016/j.nuclphysb.2019.114675, arXiv:1808.08972]
See also:
- Y. H. Ahn, Sin Kyu Kang, Hyun Min Lee, Towards a Model of Quarks and Leptons (arXiv:2112.13392)
In the large limit
In the large N limit:
-
Edward Witten, Baryons in the Expansion, Nucl. Phys. B160 (1979) 57-115 (spire:140391, doi:10.1016/0550-3213(79)90232-3)
-
Jan Albert, Johan Henriksson, Leonardo Rastelli, Alessandro Vichi, Bootstrapping mesons at large : Regge trajectory from spin-two maximization [arXiv:2312.15013]
Last revised on August 1, 2025 at 15:33:39. See the history of this page for a list of all contributions to it.