nLab ω-meson
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
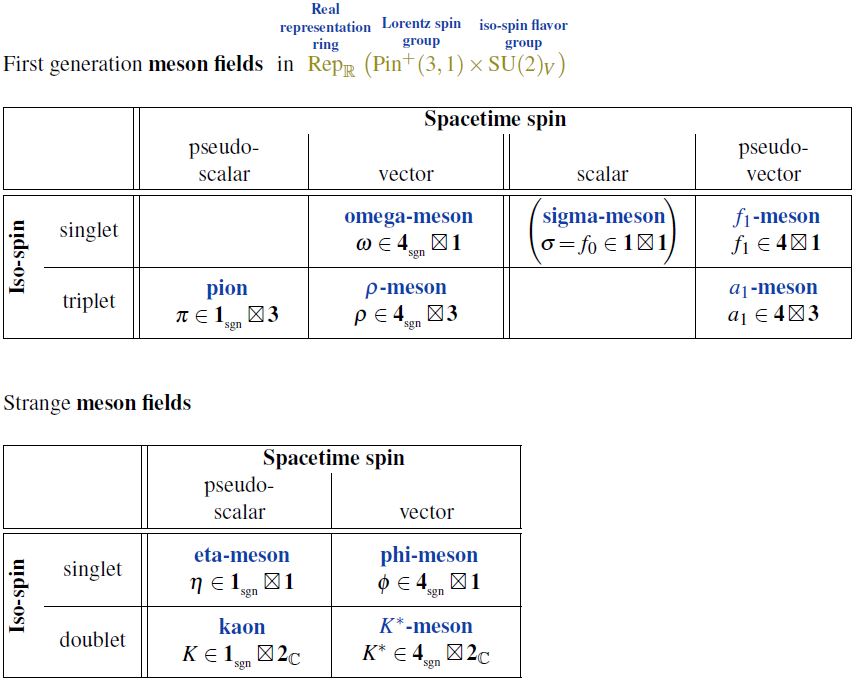
In nuclear physics, specifically in the chiral perturbation theory of quantum chromodynamics, the omega-meson is the isospin-singlet vector meson field in the first-generation of fermions, i.e. a bound state of an up quark and a down quark (a light meson), the chiral partner of the f1-meson:
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
Properties
Nuclear binding
Together with the sigma-meson the omega is responsible for most of the long-range interaction between baryons, exhibiting the residual strong nuclear force between them (as modeled by Walecka model and quantum hadrodynamics).
Couplings
The --coupling
The interaction term of the omega-meson three pions is, in the Lagrangian density, given by contraction
with the chirally anomalous baryon current , with is the exponential of the pion-field (Adkins-Nappi 84, (1) and (2), Park-Vento 09, (5.5.43) and above (5.5.50)).
This gives a decay mode
(the “charged decay”, e.g. Rudaz 84, (2)).
Or rather, this is the direct (contact term) decay. The net process is dominated by the successive decay
The ---coupling
Then there is an ω-ρ-π-coupling given by the anomalous part of the chiral WZW-term:
(e.g. Renard 69, Meissner-Kaiser-Weise 87, (2.18) Volkov-Ebert-Nagy 97, p. 12, Guetta-Singer 00, (1), Kaiser 00, (12), GKSY 03, (1) Gudino-Sanchez 12, (1))
The radiative decays
Then there is the “neutral decay”
seen in experiment as
(Nambu 57, (a), FFHNR 67, Dolinsky et al. 89, (5))
Related concepts
References
General
The -meson was first postulated by
- Yoichiro Nambu, Possible Existence of a Heavy Neutral Meson, Phys. Rev. 106, 1366 (1957) (doi:10.1103/PhysRev.106.1366)
as reviewed in
-
Jun John Sakurai, p. 48-49 of: Currents and Mesons, Chicago Lectures in Physics, based on notes by George Barry, University of Chicago Press (1969) (ISBN: 9780226733838)
(in the context of vector meson dominance)
See also:
- Wikipedia, Omega meson
See also
- Reinhard Alkofer, H. Reinhardt, H. Weigel, U. Zuckert, The Isoscalar vector meson omega in the Nambu-Jona-Lasinio soliton, Phys. Lett. B298 (1992) 132-140 (spire:343052, doi:10.1016/0370-2693(93)91719-4)
Phenomenology:
-
Cheng-Qun Pang, Ya-Rong Wang, Jing-Fu Hu, Tian-Jie Zhang, Xiang Liu, Study of the meson family and newly observed -like state (arXiv:1910.12408)
-
M. K. Volkov, A. A. Pivovarov, K. Nurlan, On the mixing angle of the vector mesons and (arXiv:2005.00763)
Decays
The direct decay :
-
S. Rudaz, Anomalies, vector mesons and the contact term, Phys. Lett. B 145 (1984) 281-284 (spire:208193, doi:10.1016/0370-2693(84)90355-1)
-
E. A. Kuraev, Z. K. Silagadze, Once more about the contact term, Phys. Atom. Nucl. 58:1589-1596, 1995 (arXiv:hep-ph/9502406)
-
M. Albaladejo, I. Danilkin, S. Gonzalez-Solis, D. Winney, C. Fernandez-Ramirez, A. N. Hiller Blin, V. Mathieu, M. Mikhasenko, A. Pilloni, A. Szczepaniak, and transition form factor revisited (arXiv:2006.01058)
The -coupling
- D. Garcia Gudino, G. Toledo Sanchez, The coupling in the VMD model revisited, Int. J. Mod. Phys. A 27, 1250101 (2012) (arXiv:1106.1467)
On Dalitz decays of omega-mesons:
-
Mirko Wachs, Die Selbstenergie des Omega-Mesons, 2000 (epda:000050)
-
Henning Berghäuser, Investigation of the Dalitz decays and the electromagnetic form factors of the and -meson, 2010 (spire:1358057)
Skyrme hadrodynamics with vector mesons (---model)
Inclusion of vector mesons (omega-meson and rho-meson/A1-meson) into the Skyrmion model of quantum hadrodynamics, in addition to the pion:
First, on the equivalence between hidden local symmetry- and massive Yang-Mills theory-description of Skyrmion quantum hadrodynamics:
- Atsushi Hosaka, H. Toki, Wolfram Weise, Skyrme Solitons With Vector Mesons: Equivalence of the Massive Yang-Mills and Hidden Local Symmetry Scheme, 1988, Z. Phys. A332 (1989) 97-102 (spire:24079)
See also
- Marcelo Ipinza, Patricio Salgado-Rebolledo, Meron-like topological solitons in massive Yang-Mills theory and the Skyrme model (arXiv:2005.04920)
Inclusion of the -meson
Original proposal for inclusion of the ω-meson in the Skyrme model:
- Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
Relating to nucleon-scattering:
- J. M. Eisenberg, A. Erell, R. R. Silbar, Nucleon-nucleon force in a skyrmion model stabilized by omega exchange, Phys. Rev. C 33, 1531 (1986) (doi:10.1103/PhysRevC.33.1531)
Combination of the omega-meson-stabilized Skyrme model with the bag model for nucleons:
- Atsushi Hosaka, Omega stabilized chiral bag model with a surface coupling, Nuclear Physics A Volume 546, Issue 3, 31 (1992) Pages 493-508 (doi:10.1016/0375-9474(92)90544-T)
Discussion of nucleon phenomenology for the -stabilized Skyrme model:
-
Sven Bjarke Gudnason, James Martin Speight, Realistic classical binding energies in the -Skyrme model (arXiv:2004.12862)
-
Derek Harland, Paul Leask, Martin Speight, Skyrmion crystals stabilized by -mesons [arXiv:2404.11287]
Inclusion of the -meson
Original proposal for inclusion of the ρ-meson:
-
Y. Igarashi, M. Johmura, A. Kobayashi, H. Otsu, T. Sato, S. Sawada, Stabilization of Skyrmions via -Mesons, Nucl.Phys. B259 (1985) 721-729 (spire:213451, doi:10.1016/0550-3213(85)90010-0)
-
Gregory Adkins, Rho mesons in the Skyrme model, Phys. Rev. D 33, 193 (1986) (spire:16895, doi:10.1103/PhysRevD.33.193)
Discussion for phenomenology of light atomic nuclei:
-
Carlos Naya, Paul Sutcliffe, Skyrmions and clustering in light nuclei, Phys. Rev. Lett. 121, 232002 (2018) (arXiv:1811.02064)
-
Carlos Naya, Paul Sutcliffe, Skyrmions in models with pions and rho, JHEP 05 (2018) 174 (arXiv:1803.06098)
APS Synopsis: Revamping the Skyrmion Model, 2018
See also:
- Miguel Huidobro, Paul Leask, Carlos Naya, Andrzej Wereszczynski, Compressibility of dense nuclear matter in the -meson variant of the Skyrme model [arXiv:2405.20757]
Inclusion of the - and -meson
The resulting -- model:
-
Ulf-G. Meissner, Ismail Zahed, Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
(includes also the A1-meson)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, Norbert Kaiser, Andreas Wirzba, Wolfram Weise, Skyrmions with and Mesons as Dynamical Gauge Bosons, Phys. Rev. Lett. 57, 1676 (1986) (doi:10.1103/PhysRevLett.57.1676)
-
Ulf-G. Meissner, Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
L. Zhang, Nimai C. Mukhopadhyay, Baryon physics from mesons: Leading order properties of the nucleon and in the chiral soliton model, Phys. Rev. D 50, 4668 (1994) (doi:10.1103/PhysRevD.50.4668, spire:384906)
-
Yong-Liang Ma, Ghil-Seok Yang, Yongseok Oh, Masayasu Harada, Skyrmions with vector mesons in the hidden local symmetry approach, Phys. Rev. D87:034023, 2013 (arXiv:1209.3554)
-
Ju-Hyun Jung, Ulugbek T. Yakhshiev, Hyun-Chul Kim, In-medium modified -- mesonic Lagrangian and properties of nuclear matter, Physics Letters B Volume 723, Issues 4–5, 25 June 2013, Pages 442-447 (arXiv:1212.4616, doi:10.1016/j.physletb.2013.05.042)
-
Ju-Hyun Jung, Ulugbek Yakhshiev, Hyun-Chul Kim, Peter Schweitzerm, In-medium modified energy-momentum tensor form factors of the nucleon within the framework of a -- soliton model, Phys. Rev. D 89, 114021 (2014) (arXiv:1402.0161)
-
Yongseok Oh, Skyrmions with vector mesons revisited (arXiv:1402.2821)
See also
- Ki-Hoon Hong, Ulugbek Yakhshiev, Hyun-Chul Kim, Modification of hyperon masses in nuclear matter, Phys. Rev. C 99, 035212 (2019) (arXiv:1806.06504)
Review:
-
Roland Kaiser, Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
-
Gottfried Holzwarth, Section 2.3 of: Electromagnetic Form Factors of the Nucleon in Chiral Soliton Models (arXiv:hep-ph/0511194), Chapter 2 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Yongseok Oh, Skyrmions with vector mesons: Single Skyrmion and baryonic matter, 2013 (pdf)
Combination of the omega-rho-Skyrme model with the bag model of quark confinement:
- H. Takashita, S. Yoro, H. Toki, Chiral bag plus skyrmion hybrid model with vector mesons for nucleon, Nuclear Physics A Volume 485, Issues 3–4, August 1988, Pages 589-605 (doi:10.1016/0375-9474(88)90555-6)
Inclusion of the -meson
Inclusion of the sigma-meson:
- Thomas D. Cohen, Explicit meson, topology, and the large- limit of the Skyrmion, Phys. Rev. D 37 (1988) (doi:10.1103/PhysRevD.37.3344)
For analysis of neutron star equation of state:
- David Alvarez-Castillo, Alexander Ayriyan, Gergely Gábor Barnaföldi, Hovik Grigorian, Péter Pósfay, Studying the parameters of the extended - model for neutron star matter (arXiv:2006.03676)
Couplings
On omega-meson interactions and decay modes:
-
Stanley M. Flatté, Darrell O. Huwe, Joseph J. Murray, Janice Button-Shafer, Frank T. Solmitz, M. Lynn Stevenson, and Charles Wohl, Decay Properties of the Meson, Phys. Rev. 145, 1050 – Published 27 May 1966 (doi:10.1103/PhysRev.145.1050)
-
M. Feldman, W. Frati, R. Gleeson, J. Halpern, M. Nussbaum, S. Richert, Neutral Decay of the Meson, Phys. Rev. 159, 1219 (1967) (doi10.1103/PhysRev.159.1219, spire:52556)
-
W. Deinet A. Menzione H.Müller, H. M.Staudenmaier, S.Buniatov, D.Schmitt, Neutral decay modes of the -meson, Physics Letters B Volume 30, Issue 6, 10 November 1969, Pages 426-429 (doi:10.1016/0370-2693(69)90479-1)
-
F. M. Renard, The reaction and the -- coupling, Nuovo Cimento A (1965-1970) 64, 979–984 (1969) (doi:10.1007/BF02758844)
-
M. K. Volkov, D. Ebert, M. Nagy, Excited pions, - and -mesons and their decays in a chiral Lagrangian, Int. J. Mod. Phys. A13 (1998) 5443-5458 (arXiv:hep-ph/9705334)
-
S. I. Dolinsky, et al., Radiative Decays of and Mesons, Z. Phys. C42 (1989) 511 (spire:264694, doi:10.1007/BF01557655)
-
J. T. Dakin, M. G. Hauser, M. N. Kreisler, R. E. Mischke, Measurement of the Branching Ratios for ω Neutral Decays, Phys. Rev. D 6, 2321 (1972) (doi:10.1103/PhysRevD.6.2321)
-
Dafne Guetta, Paul Singer, - Mixing and the Decay, Phys. Rev. D63 (2001) 017502 (arXiv:hep-ph/0005059)
-
Roland Kaiser, equation (12) of: Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377)
-
A. Gokalp, A. Kucukarslan, S. Solmaz, O. Yilmaz, -Meson and - mixing effects in decay, Acta Phys.Polon. B34 (2003) 4095-4104 (arXiv:hep-ph/0306044)
-
Jeffrey Harvey, Christopher T. Hill, Richard J. Hill, Section II.B of: Standard Model Gauging of the WZW Term: Anomalies, Global Currents and pseudo-Chern-Simons Interactions, Phys. Rev. D77:085017, 2008 (arXiv:0712.1230)
-
S. Leupold, M. F. M. Lutz, Hadronic three-body decays of light vector mesons, Eur. Phys. J. A39:205-212, 2009 (arXiv:0807.4686)
-
Florian Jonas, Measurement of and mesons via their three pion decay with ALICE in pp collisions at , 2018 (cds:2653176)
In holographic QCD
The omega-meson in holographic QCD (Witten-Sakai-Sugimoto model):
- Tadakatsu Sakai, Shigeki Sugimoto, Section 4.3 of: More on a holographic dual of QCD, Progr. Theor. Phys. 114: 1083-1118, 2005 (arXiv:hep-th/0507073)
Mediating baryon interaction
On sigma-mesons and omega-mesons mediating baryon interaction, discussed in holographic QCD via D3-D7 brane intersections:
- Anatoly Dymarsky, Dmitry Melnikov, Jacob Sonnenschein, Attractive Holographic Baryons, JHEP 06 (2011) 145 (arXiv:1012.1616)
Last revised on June 2, 2020 at 18:20:50. See the history of this page for a list of all contributions to it.