nLab chiral perturbation theory
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
- Idea
- Properties
- Relation to the Skyrme model
- Baryon Chiral Perturbation Theory
- Partially Quenched Chiral Perturbation Theory
- Random Matrix Theory and Chiral Symmetry
- Related concepts
- References
- Introduction and review
- Original articles
- Skyrme hadrodynamics with vector mesons (---model)
- Inclusion of the -meson
- Inclusion of the -meson
- Inclusion of the - and -meson
- Inclusion of the -meson
- Skyrme hadrodynamics with heavy quarks/mesons
- Inclusion of strange quarks/kaons
- Inclusion of charm quarks/D-mesons
- Inclusion of bottom quarks/B-mesons
- The WZW term of QCD chiral perturbation theory
- General
- Including light vector mesons
- Including heavy scalar mesons
- Including heavy vector mesons
- Including electroweak interactions
- Baryon chiral perturbation theory
- Applications to lattice QCD
- Inclusion of leptons
- Antisymmetric tensor representation for vector mesons
Idea
What is called chiral perturbation theory in quantum field theory of nuclear physics is the effective field theory of quantum chromodynamics in the confined sector, where the effective fields are hadrons:
-
lightscalar mesons appear as the Goldstone bosons of the spontaneously broken chiral symmetry (see below),
-
vector mesons appear as gauge fields of a hidden local symmetry,
-
baryons (specifically nuclei) appear as solitons in the meson-fields (called Skyrmions),
-
heavy mesons appear as further fields.
Hence some authors also speak of quantum hadrodynamics.
More concretely, chiral perturbation theory is perturbation theory not in the coupling constant of QCD, but in the masses of the light quarks, which in practice means: of the up quark and the down quark and possibly also of the strange quark, with masses , and , respectively.
As such, the point about which perturbations are considered in chiral perturbation theory of QCD is that of vanishing quark masses, hence the limit .
Notice that the proton mass (the characteristic scale of QCD witnessing its confinement/mass gap-property, see e.g. Roberts 21) is much larger than the sum of its constituent quarks
suggesting that is a good limit around which to inspect the hadronic bound states of QCD.
But since only the quark mass term in the Lagrangian density of QCD mixes the two chiralities of quarks, its Lagrangian density in this massless limit is the sum of a term that only contains the left-chiral quark spinors, and an analogous summand that only contains the right-chiral quark spinors (e.g. Ecker 95, (2.1)):
(here denotes the quark Dirac field with left and right chiral Weyl spinor components and , denotes the Dirac operator, the gluon field (in Feynman slash notation), and the field strength of the gluon field – see at Yang-Mills theory for more).
Moreover, all two (up and down) or even all three (if including strange) flavours of quarks enter each of these two spinor-chiral summands symmetrically, such that each of them has SU(2) or respectively SU(3) global symmetry, acting by mixing the quark flavours. This yields a total direct product symmetry group
where is the number of flavours of light quarks that are being considered, and where the subscripts indicate the left/right-handed chiral spinor-components of quarks whose flavours are being mixed by these group actions. This symmetry group is hence also called chiral symmetry. Accordingly, its symmetry breaking to the diagonal subgroup
(the subscript “” is for “vector”) either explicitly by positive quark masses or spontaneously by a vacuum expectation value , is called chiral symmetry breaking. This is the origin of the termchiral perturbation theory_.
Additionally, the application of noether's theorem? to the classical global symmetry of the lagrangian density in the chiral limit yields conserved currents, via the method of Gell-Mann? and Levy?. Namely, the promotion of the global symmetry inherent in the lagrangian density to a local symmetry allows us to identify these conserved noether currents?
(…)
Properties
Relation to the Skyrme model
Relation to Skyrmions:
- Dmitri Diakonov, Victor Petrov, Exotic baryon resonances in the Skyrme model (arXiv:0812.1212, doi:10.1142/9789814704410_0004), Chapter 3 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
It is astounding that Skyrme had suggested his model as early as in 1961 before it has been generally accepted that pions are (pseudo) Goldstone bosons associated with the spontaneous breaking of chiral symmetry, and of course long before Quantum Chromodynamics (QCD) has been put forward as the microscopic theory of strong interactions.
The revival of the Skyrme idea in 1983 is due to Witten who explained the raison d’ˆetre of the Skyrme model from the viewpoint of QCD. In the chiral limit when the light quark masses , , tend to zero, such that the octet of the pseudoscalar mesons π, K , η become nearly massless (pseudo) Goldstone bosons, they are the lightest degrees of freedom of QCD. The effective chiral Lagrangian (EχL) for pseudoscalar mesons, understood as an infinite expansion in the derivatives of the pseudoscalar (or chiral) fields, encodes, in principle, full information about QCD. The famous two-term Skyrme Lagrangian can be understood as a low-energy truncation of this infinite series. Witten has added an important four-derivative Wess–Zumino term to the original Skyrme Lagrangian and pointed out that the overall coefficient in front of the EχL is proportional to the number of quark colours .
Soon after Witten’s work it has been realized that it is possible to bring the Skyrme model and the Skyrmion even closer to QCD and to the more customary language of constituent quarks. It has been first noticed 6, 7a, 7b, 8 that a simple chiral invariant Lagrangian for massive (constituent) quarks interacting with the octet chiral field ,
induces, via a quark loop in the external pseudoscalar fields (see Fig. 3.1), the EχL whose lowest-derivative terms coincide with the Skyrme Lagrangian, including automatically the Wess–Zumino term, with the correct coefficient!
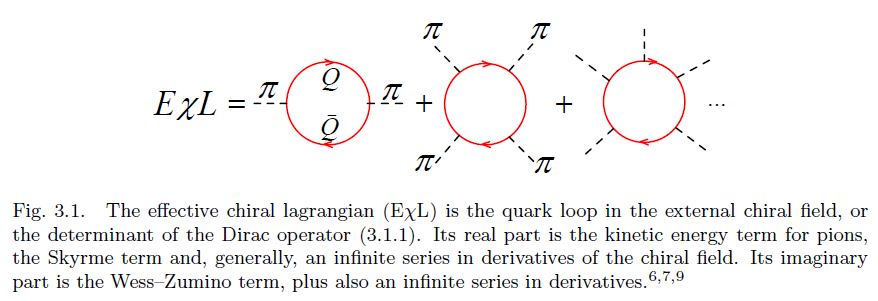
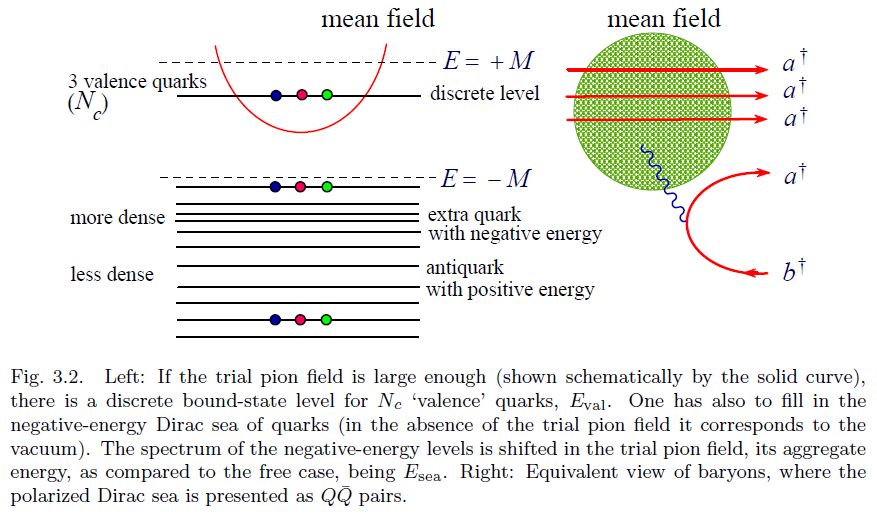
The condition that the winding number of the trial field is unity needs to be imposed to get a deeply bound state, that is to guarantee that the baryon number is unity. 9 The Skyrmion is, thus, nothing but the mean chiral field binding quarks in a baryon.
-
Dmitri Diakonov, Michael I. Eides, Chiral Lagrangian from a functional integral over quarks, JETP Letters 38.7 (1983): 433-436 (pdf, pdf)
-
A. Dhar, Spenta R. Wadia, Nambu—Jona-Lasinio Model: An Effective Lagrangian for Quantum Chromodynamics at Intermediate Length Scales, Phys. Rev. Lett. 52, 959 (1984) (doi:10.1103/PhysRevLett.52.959)
-
Avinash Dhar, R. Shankar, Spenta R. Wadia, Nambu–Jona-Lasinio–type effective Lagrangian: Anomalies and nonlinear Lagrangian of low-energy, large-N QCD, Phys. Rev. D 31, 3256 (1985) (doi:10.1103/PhysRevD.31.3256)
-
Dmitri Diakonov, Victor Petrov, A theory of light quarks in the instanton vacuum, Nuclear Physics B Volume 272, Issue 2, 21 July 1986, Pages 457-489 (doi:10.1016/0550-3213(86)90011-8)
-
Dmitri Diakonov, Victor Petrov, P.V. Pobylitsa, A Chiral Theory of Nucleons, Nucl. Phys. B306 (1988) 809 (spire:247700, doi:10.1016/0550-3213(88)90443-9)
-
Nicholas S. Manton, Robustness of the Hedgehog Skyrmion [arXiv:2405.05731]
Baryon Chiral Perturbation Theory
The QCD vacuum breaks chiral symmetry down to the diagonal subgroup of SU(3), , whereby 8 massless goldstone bosons appear, each of which are coupled via to the conserved axial-vector current. The physics of these goldstone bosons, which are themselves the pion fields, describe the low energry effective field theory known as chiral perturbation theory. In this low energy structure of QCD, heavy quarks do not play a role since their degrees of freedom are frozen at low energies. However, when the baryon fields are treated as heavy static fermions in the expansion of the physical vacuum state of QCD, one can write the effective theory in terms of baryon fields with a definite velocity, . In the heavy baryon limit, the most general Lagrangian at leading-order is
Partially Quenched Chiral Perturbation Theory
In Lattice QCD?, it is notoriously difficult to include the loops of light quarks. One remedy to this problem is to approximate the fermion determinant of a Dirac operator , which is proportional to the summation of external sources interacting with one internal fermion loop?. The partially quenched prescription includes the determinant but with sea quark? masses those of the valence quarks. The simulation of partially quenched QCD (PQQCD) on the lattice can yield information about QCD itself by utilizing chiral perturbation theory. The formulation of XPT in PQQCD is difficult compared to the unquenched case (standard formulation) due to the lack of a physical hilbert space?.
-
S.R.Sharpe and N.Shoresh, Partially quenched chiral perturbation theory without Phi0, Phys. Rev. D 64, 114510 (2001), doi:10.1103/PhysRevD.64.114510, (arXiv:hep-lat/0108003)
-
Claude W. Bernard and Maarten F. L. Golterman, Partially quenched gauge theories and an application to staggered fermions, Phys. Rev. D 49, 486 – Published 1 January 1994, (doi:10.1103/486)
Random Matrix Theory and Chiral Symmetry
It has been posited that the statistics of the low-lying eigenvalues of the QCD Dirac operator can be described by a random matrix theory with the global symmetries of the QCD partition function.
-
J.J.M. Verbaarschot and T.Wettig, Random matrix theory and chiral symmetry in QCD, Ann. Rev. Nucl. Part. Sci. 50, 343-410 (2000), doi:10.1146/annurev.nucl.50.1.343, (arXiv:hep-ph/0003017 [hep-ph]).
-
J.C. Osborn, D.Toublan and J.J.M.Verbaarschot, From chiral random matrix theory to chiral perturbation theory, Nucl. Phys. B 540, 317-344 (1999), doi:10.1016/S0550-3213(98)00716-0 (arXiv:hep-th/9806110).
Related concepts
effective field theories of nuclear physics, hence for confined-phase quantum chromodynamics:
References
-
Luca Ciambriello, Roberto Contino, Andrea Luzio, Marcello Romano, Ling-Xiao Xu, A novel strategy to prove chiral symmetry breaking in QCD-like theories [arXiv:2404.02967]
-
Luca Ciambriello, Roberto Contino, Ling-Xiao Xu, On the Proof of Chiral Symmetry Breaking through Anomaly Matching in QCD-like Theories: An Exemplification [arXiv:2404.02971]
Introduction and review
-
Jürg Gasser, The QCD Vacuum and Chiral Symmetry, In: Vautherin D., Lenz F., Negele J.W. (eds.) Hadrons and Hadronic Matter, NATO ASI Series (Series B: Physics), vol 228. Springer 1990 (doi:10.1007/978-1-4684-1336-6_4)
-
Gerhard Ecker, The standard model at low energies, Czech. J. Phys. 44:405-430, 1995 (arXiv:hep-ph/9309268)
-
Gerhard Ecker, Chiral Perturbation Theory, Prog. Part. Nucl. Phys. 35:1-80, 1995 (arXiv:hep-ph/9501357)
-
Antonio Pich, Chiral Perturbation Theory (arXiv:hep-ph/9502366)
-
Maciej Nowak, Mannque Rho, Ismail Zahed, Chiral Nuclear Dynamics, World Scientific 1996 (doi:10.1142/1681)
-
Volker Koch, Aspects of Chiral Symmetry, Int. J. Mod. Phys. E6 (1997) 203-250 (arXiv:nucl-th/9706075)
-
Barry R. Holstein, A Brief Introduction to Chiral Perturbation Theory, Czech. J. Phys. 50S4:9-23, 2000 (arXiv:hep-ph/9911449)
-
Stefan Scherer, Introduction to Chiral Perturbation Theory, Adv. Nucl. Phys. 27 (2003) 277 (arXiv:hep-ph/0210398)
-
Stefan Scherer, Matthias R. Schindler, A Chiral Perturbation Theory Primer (arXiv:hep-ph/0505265)
-
Véronique Bernard, Ulf-G. Meissner, Chiral perturbation theory, Ann. Rev. Nucl. Part. Sci.57:33-60, 2007 (arXiv:hep-ph/0611231)
-
Gerhard Ecker, Status of chiral perturbation theory, PoS Confinement 8:025, 2008 (arXiv:0812.4196)
-
Johan Bijnens, Chiral perturbation theory in the meson sector, PoS CD09:031, 2009 (arXiv:0909.4635)
-
Johan Bijnens, Status of Strong ChPT, PoS EFT09 (2009) 022 (spire:818610)
-
Rupert Machleidt, David Rodríguez Entem, Chiral effective field theory and nuclear forces, Phys. Rept. 503:1-75, 2011 (arXiv:1105.2919, doi:10.1016/j.physrep.2011.02.001)
-
Franco Strocchi, §8 of: An Introduction to Non-Perturbative Foundations of Quantum Field Theory, Oxford University Press (2013) [doi:10.1093/acprof:oso/9780199671571.001.0001]
(in a context of non-perturbative quantum field theory)
-
Brambilla et al., Sections 3-4 in: QCD and strongly coupled gauge theories - challenges and perspectives, Eur Phys J C Part Fields. 2014; 74(10): 2981 (arXiv:1404.3723, doi:10.1140/epjc/s10052-014-2981-5)
-
Yong-Liang Ma, Masayasu Harada, Section II.B of: Lecture notes on the Skyrme model (arXiv:1604.04850, spire:1448311)
-
Franz Gross, Eberhard Klempt et al., Section 6.2 of: 50 Years of Quantum Chromodynamics, EJPC [arXiv:2212.11107]
-
Ulf-G. Meissner: Chiral perturbation theory, Encyclopedia of Particle Physics [arXiv:2410.21912]
-
Ulf-G. Meißner: Chiral dynamics: Quo vadis? [arXiv:2501.03014]
See also:
- Wikipedia, Chiral perturbation theory
-
Brian D. Serot, Quantum hadrodynamics, Rept.Prog.Phys. 55 (1992) 1855-1946, (spire:333292, doi:10.1088/0034-4885/55/11/001)
-
Brian D. Serot, John Dirk Walecka, Recent Progress in Quantum Hadrodynamics, Int. J. Mod. Phys. E6:515-631, 1997 (arXiv:nucl-th/9701058)
Via the S-matrix/scattering amplitudes of mesons:
-
Andrea Guerrieri, Joao Penedones, Pedro Vieira, S-matrix Bootstrap for Effective Field Theories: Massless Pions (arXiv:2011.02802)
-
Eef van Beveren, George Rupp, Modern meson spectroscopy: the fundamental role of unitarity (arXiv:2012.03693)
Original articles
-
Sidney Coleman, Julius Wess, Bruno Zumino, Structure of Phenomenological Lagrangians. I, Phys. Rev. 177, 2239 (1969) (doi:10.1103/PhysRev.177.2239)
-
Curtis Callan, Jr., Sidney Coleman, Julius Wess, Bruno Zumino, Structure of Phenomenological Lagrangians. II, Phys. Rev. 177, 2247 (1969) (doi:10.1103/PhysRev.177.2247)
-
Steven Weinberg, Phenomenological Lagrangians, Physica A: Statistical Mechanics and its Applications Volume 96, Issues 1–2, April 1979, Pages 327-340 (doi:10.1016/0378-4371(79)90223-1)
-
Gerard 't Hooft, Naturalness, Chiral Symmetry, and Spontaneous Chiral Symmetry Breaking In: G. ‘Hooft et al., Recent Developments in Gauge Theories, NATO Advanced Study Institutes Series 59, Springer (1980) [doi:10.1007/978-1-4684-7571-5_9]
-
Jürg Gasser, Heinrich Leutwyler, Quark masses, Physics Reports Volume 87, Issue 3, July 1982, Pages 77-169 (doi:10.1016/0370-1573(82)90035-7)
-
Jürg Gasser, Heinrich Leutwyler, Chiral Perturbation Theory: Expansions in the Mass of the Strange Quark, Nucl. Phys. B 250 (1985) 465-516, (spire:200027, doi:10.1016/0550-3213(85)90492-4))
-
Jürg Gasser, Heinrich Leutwyler, Chiral perturbation theory to one loop, Annals of Physics Volume 158, Issue 1, November 1984, Pages 142-210 (doi:10.1016/0003-4916(84)90242-2)
-
Gerard 't Hooft, How instantons solve the problem, Physics Reports Volume 142, Issue 6, September 1986, Pages 357-387 (doi:10.1016/0370-1573(86)90117-1)
-
Heinrich Leutwyler, On the Foundations of Chiral Perturbation Theory, Annals Phys. 235 (1994) 165-203 (arXiv:hep-ph/9311274)
At higher order:
- Nils Hermansson-Truedsson, Chiral Perturbation Theory at NNNLO (arXiv:2006.01430)
In relation to the theta vacuum (Yang-Mills instanton vacuum):
- Giovanni Morchio, Franco Strocchi, Chiral symmetry breaking and theta vacuum structure in QCD, Annals Phys. 324 (2009) 2236-2254 [arXiv:0907.2522, doi:10.1016/j.aop.2009.07.005]
Specifically for kaon decay:
- V. Cirigliano, Gerhard Ecker, Helmut Neufeld, Antonio Pich, J. Portoles, Kaon Decays in the Standard Model, Rev. Mod. Phys. 84 (2012) 399 (arXiv:1107.6001)
Further discussion of phenomenology:
-
Prabal Adhikari, Jens O. Andersen, Quark and pion condensates at finite isospin density in chiral perturbation theory (arXiv:2003.12567)
-
Bryan W. Lynn, Brian J. Coffey, Kellen E. McGee, Glenn D. Starkman, Nuclear matter as a liquid phase of spontaneously broken semi-classical chiral perturbation theory: Static chiral nucleon liquids (arXiv:2004.01706)
See also
-
Yu-Jia Wang, Feng-Kun Guo, Cen Zhang, Shuang-Yong Zhou, Generalized positivity bounds on chiral perturbation theory (arXiv:2004.03992)
-
Lukas Graf, Brian Henning, Xiaochuan Lu, Tom Melia, Hitoshi Murayama, 2, 12, 117, 1959, 45171, 1170086, …: A Hilbert series for the QCD chiral Lagrangian (arXiv:2009.01239)
Skyrme hadrodynamics with vector mesons (---model)
Inclusion of vector mesons (omega-meson and rho-meson/A1-meson) into the Skyrmion model of quantum hadrodynamics, in addition to the pion:
First, on the equivalence between hidden local symmetry- and massive Yang-Mills theory-description of Skyrmion quantum hadrodynamics:
- Atsushi Hosaka, H. Toki, Wolfram Weise, Skyrme Solitons With Vector Mesons: Equivalence of the Massive Yang-Mills and Hidden Local Symmetry Scheme, 1988, Z. Phys. A332 (1989) 97-102 (spire:24079)
See also
- Marcelo Ipinza, Patricio Salgado-Rebolledo, Meron-like topological solitons in massive Yang-Mills theory and the Skyrme model (arXiv:2005.04920)
Inclusion of the -meson
Original proposal for inclusion of the ω-meson in the Skyrme model:
- Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
Relating to nucleon-scattering:
- J. M. Eisenberg, A. Erell, R. R. Silbar, Nucleon-nucleon force in a skyrmion model stabilized by omega exchange, Phys. Rev. C 33, 1531 (1986) (doi:10.1103/PhysRevC.33.1531)
Combination of the omega-meson-stabilized Skyrme model with the bag model for nucleons:
- Atsushi Hosaka, Omega stabilized chiral bag model with a surface coupling, Nuclear Physics A Volume 546, Issue 3, 31 (1992) Pages 493-508 (doi:10.1016/0375-9474(92)90544-T)
Discussion of nucleon phenomenology for the -stabilized Skyrme model:
-
Sven Bjarke Gudnason, James Martin Speight, Realistic classical binding energies in the -Skyrme model (arXiv:2004.12862)
-
Derek Harland, Paul Leask, Martin Speight, Skyrmion crystals stabilized by -mesons [arXiv:2404.11287]
Inclusion of the -meson
Original proposal for inclusion of the ρ-meson:
-
Y. Igarashi, M. Johmura, A. Kobayashi, H. Otsu, T. Sato, S. Sawada, Stabilization of Skyrmions via -Mesons, Nucl.Phys. B259 (1985) 721-729 (spire:213451, doi:10.1016/0550-3213(85)90010-0)
-
Gregory Adkins, Rho mesons in the Skyrme model, Phys. Rev. D 33, 193 (1986) (spire:16895, doi:10.1103/PhysRevD.33.193)
Discussion for phenomenology of light atomic nuclei:
-
Carlos Naya, Paul Sutcliffe, Skyrmions and clustering in light nuclei, Phys. Rev. Lett. 121, 232002 (2018) (arXiv:1811.02064)
-
Carlos Naya, Paul Sutcliffe, Skyrmions in models with pions and rho, JHEP 05 (2018) 174 (arXiv:1803.06098)
APS Synopsis: Revamping the Skyrmion Model, 2018
See also:
- Miguel Huidobro, Paul Leask, Carlos Naya, Andrzej Wereszczynski, Compressibility of dense nuclear matter in the -meson variant of the Skyrme model [arXiv:2405.20757]
Inclusion of the - and -meson
The resulting -- model:
-
Ulf-G. Meissner, Ismail Zahed, Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
(includes also the A1-meson)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, Norbert Kaiser, Andreas Wirzba, Wolfram Weise, Skyrmions with and Mesons as Dynamical Gauge Bosons, Phys. Rev. Lett. 57, 1676 (1986) (doi:10.1103/PhysRevLett.57.1676)
-
Ulf-G. Meissner, Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
L. Zhang, Nimai C. Mukhopadhyay, Baryon physics from mesons: Leading order properties of the nucleon and in the chiral soliton model, Phys. Rev. D 50, 4668 (1994) (doi:10.1103/PhysRevD.50.4668, spire:384906)
-
Yong-Liang Ma, Ghil-Seok Yang, Yongseok Oh, Masayasu Harada, Skyrmions with vector mesons in the hidden local symmetry approach, Phys. Rev. D87:034023, 2013 (arXiv:1209.3554)
-
Ju-Hyun Jung, Ulugbek T. Yakhshiev, Hyun-Chul Kim, In-medium modified -- mesonic Lagrangian and properties of nuclear matter, Physics Letters B Volume 723, Issues 4–5, 25 June 2013, Pages 442-447 (arXiv:1212.4616, doi:10.1016/j.physletb.2013.05.042)
-
Ju-Hyun Jung, Ulugbek Yakhshiev, Hyun-Chul Kim, Peter Schweitzerm, In-medium modified energy-momentum tensor form factors of the nucleon within the framework of a -- soliton model, Phys. Rev. D 89, 114021 (2014) (arXiv:1402.0161)
-
Yongseok Oh, Skyrmions with vector mesons revisited (arXiv:1402.2821)
See also
- Ki-Hoon Hong, Ulugbek Yakhshiev, Hyun-Chul Kim, Modification of hyperon masses in nuclear matter, Phys. Rev. C 99, 035212 (2019) (arXiv:1806.06504)
Review:
-
Roland Kaiser, Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
-
Gottfried Holzwarth, Section 2.3 of: Electromagnetic Form Factors of the Nucleon in Chiral Soliton Models (arXiv:hep-ph/0511194), Chapter 2 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
-
Yongseok Oh, Skyrmions with vector mesons: Single Skyrmion and baryonic matter, 2013 (pdf)
Combination of the omega-rho-Skyrme model with the bag model of quark confinement:
- H. Takashita, S. Yoro, H. Toki, Chiral bag plus skyrmion hybrid model with vector mesons for nucleon, Nuclear Physics A Volume 485, Issues 3–4, August 1988, Pages 589-605 (doi:10.1016/0375-9474(88)90555-6)
Inclusion of the -meson
Inclusion of the sigma-meson:
- Thomas D. Cohen, Explicit meson, topology, and the large- limit of the Skyrmion, Phys. Rev. D 37 (1988) (doi:10.1103/PhysRevD.37.3344)
For analysis of neutron star equation of state:
- David Alvarez-Castillo, Alexander Ayriyan, Gergely Gábor Barnaföldi, Hovik Grigorian, Péter Pósfay, Studying the parameters of the extended - model for neutron star matter (arXiv:2006.03676)
Skyrme hadrodynamics with heavy quarks/mesons
Inclusion of heavy flavors into the Skyrme model for quantum hadrodynamics:
Inclusion of strange quarks/kaons
Inclusion of strange quarks/kaons into the Skyrme model:
-
Curtis Callan, Igor Klebanov, Bound-state approach to strangeness in the Skyrme model, Nuclear Physics B Volume 262, Issue 2, 16 December 1985, Pages 365-382 (doi10.1016/0550-3213(85)90292-5)
-
Curtis Callan, K. Hornbostel, Igor Klebanov, Baryon masses in the bound state approach to strangeness in the skyrme model, Physics Letters B Volume 202, Issue 2, 3 March 1988, Pages 269-275 (doi10.1016/0370-2693(88)90022-6)
-
Norberto Scoccola, D. P. Min, H. Nadeau, Mannque Rho, The strangeness problem: An skyrmion with vector mesons, Nuclear Physics A Volume 505, Issues 3–4, 25 December 1989, Pages 497-524 (doi:10.1016/0375-9474(89)90029-8)
Review:
-
Igor Klebanov, section 6 of: Strangeness in the Skyrme model, in: D. Vauthrin, F. Lenz, J. W. Negele, Hadrons and Hadronic Matter, Plenum Press 1989 (doi:10.1007/978-1-4684-1336-6)
-
Mannque Rho, Section 2.2 of: Cheshire Cat Hadrons, Phys. Rept. 240 (1994) 1-142 (arXiv:hep-ph/9310300, doi:10.1016/0370-1573(94)90002-7)
Inclusion of charm quarks/D-mesons
Inclusion of charm quarks/D-mesons into the Skyrme model:
-
Mannque Rho, D. O. Riska, Norberto Scoccola, Charmed baryons as soliton - D meson bound states, Phys. Lett.B 251 (1990) 597-602 (spire:297771, doi:10.1016/0370-2693(90)90802-D)
-
Yongseok Oh, Dong-Pil Min, Mannque Rho, Norberto Scoccola, Massive-quark baryons as skyrmions: Magnetic moments, Nuclear Physics A Volume 534, Issues 3–4 (1991) Pages 493-512 (doi:10.1016/0375-9474(91)90458-I)
Inclusion of bottom quarks/B-mesons
Inclusion of further heavy flavors beyond strange quark/kaons, namely charm quarks/D-mesons and bottom quarks/B-mesons, into the Skyrme model:
-
Mannque Rho, D. O. Riska, Norberto Scoccola, The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages 343–352 (1992) (doi:10.1007/BF01283544)
-
Arshad Momen, Joseph Schechter, Anand Subbaraman, Heavy Quark Solitons: Strangeness and Symmetry Breaking, Phys. Rev. D49:5970-5978, 1994 (arXiv:hep-ph/9401209)
-
Yongseok Oh, Byung-Yoon Park, Dong-Pil Min, Heavy Baryons as Skyrmion with Corrections, Phys. Rev. D49 (1994) 4649-4658 (arXiv:hep-ph/9402205)
Review:
-
Mannque Rho, Massive-quark baryons as Skyrmions, Modern Physics Letters A, Vol. 06, No. 23 (1991) (doi:10.1142/S0217732391002268)
-
Norberto Scoccola, Heavy quark skyrmions, (arXiv:0905.2722, doi:10.1142/9789814280709_0004), Chapter 4 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
The WZW term of QCD chiral perturbation theory
The gauged WZW term of chiral perturbation theory/quantum hadrodynamics which reproduces the chiral anomaly of QCD in the effective field theory of mesons and Skyrmions:
General
The original articles:
-
Julius Wess, Bruno Zumino, Consequences of anomalous Ward identities, Phys. Lett. B 37 (1971) 95-97 (spire:67330, doi:10.1016/0370-2693(71)90582-X)
-
Edward Witten, Global aspects of current algebra, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 422-432 (doi:10.1016/0550-3213(83)90063-9)
See also:
- O. Kaymakcalan, S. Rajeev, J. Schechter, Nonabelian Anomaly and Vector Meson Decays, Phys. Rev. D 30 (1984) 594 (spire:194756)
Corrections and streamlining of the computations:
-
Chou Kuang-chao, Guo Han-ying, Wu Ke, Song Xing-kang, On the gauge invariance and anomaly-free condition of the Wess-Zumino-Witten effective action, Physics Letters B Volume 134, Issues 1–2, 5 January 1984, Pages 67-69 (doi:10.1016/0370-2693(84)90986-9))
-
H. Kawai, S.-H. H. Tye, Chiral anomalies, effective lagrangians and differential geometry, Physics Letters B Volume 140, Issues 5–6, 14 June 1984, Pages 403-407 (doi:10.1016/0370-2693(84)90780-9)
-
J. L. Mañes, Differential geometric construction of the gauged Wess-Zumino action, Nuclear Physics B Volume 250, Issues 1–4, 1985, Pages 369-384 (doi:10.1016/0550-3213(85)90487-0)
-
Tomáš Brauner, Helena Kolešová, Gauged Wess-Zumino terms for a general coset space, Nuclear Physics B Volume 945, August 2019, 114676 (doi:10.1016/j.nuclphysb.2019.114676)
See also
- Yasunori Lee, Kantaro Ohmori, Yuji Tachikawa, Revisiting Wess-Zumino-Witten terms (arXiv:2009.00033)
Interpretation as Skyrmion/baryon current:
-
Jeffrey Goldstone, Frank Wilczek, Fractional Quantum Numbers on Solitons, Phys. Rev. Lett. 47, 986 (1981) (doi:10.1103/PhysRevLett.47.986)
-
Edward Witten, Current algebra, baryons, and quark confinement, Nuclear Physics B Volume 223, Issue 2, 22 August 1983, Pages 433-444 (doi:10.1016/0550-3213(83)90064-0)
-
Gregory Adkins, Chiara Nappi, Stabilization of Chiral Solitons via Vector Mesons, Phys. Lett. 137B (1984) 251-256 (spire:194727, doi:10.1016/0370-2693(84)90239-9)
(beware that the two copies of the text at these two sources differ!)
-
Mannque Rho et al., Introduction, In: Mannque Rho et al. (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Concrete form for -flavor quantum hadrodynamics in 2d:
- C. R. Lee, H. C. Yen, A Derivation of The Wess-Zumino-Witten Action from Chiral Anomaly Using Homotopy Operators, Chinese Journal of Physics, Vol 23 No. 1 (1985) (spire:16389, pdf)
Concrete form for 2 flavors in 4d:
- Masashi Wakamatsu, On the electromagnetic hadron current derived from the gauged Wess-Zumino-Witten action, (arXiv:1108.1236, spire:922302)
Including light vector mesons
Concrete form for 2-flavor quantum hadrodynamics in 4d with light vector mesons included (omega-meson and rho-meson):
-
Ulf-G. Meissner, Ismail Zahed, equation (6) in: Skyrmions in the Presence of Vector Mesons, Phys. Rev. Lett. 56, 1035 (1986) (doi:10.1103/PhysRevLett.56.1035)
-
Ulf-G. Meissner, Norbert Kaiser, Wolfram Weise, equation (2.18) in: Nucleons as skyrme solitons with vector mesons: Electromagnetic and axial properties, Nuclear Physics A Volume 466, Issues 3–4, 11–18 May 1987, Pages 685-723 (doi:10.1016/0375-9474(87)90463-5)
-
Ulf-G. Meissner, equation (2.45) in: Low-energy hadron physics from effective chiral Lagrangians with vector mesons, Physics Reports Volume 161, Issues 5–6, May 1988, Pages 213-361 (doi:10.1016/0370-1573(88)90090-7)
-
Roland Kaiser, equation (12) in: Anomalies and WZW-term of two-flavour QCD, Phys. Rev. D63:076010, 2001 (arXiv:hep-ph/0011377, spire:537600)
Including heavy scalar mesons
Including heavy scalar mesons:
specifically kaons:
-
Curtis Callan, Igor Klebanov, equation (4.1) in: Bound-state approach to strangeness in the Skyrme model, Nuclear Physics B Volume 262, Issue 2, 16 December 1985, Pages 365-382 (doi10.1016/0550-3213(85)90292-5)
-
Igor Klebanov, equation (99) of: Strangeness in the Skyrme model, in: D. Vauthrin, F. Lenz, J. W. Negele, Hadrons and Hadronic Matter, Plenum Press 1989 (doi:10.1007/978-1-4684-1336-6)
-
N. N. Scoccola, D. P. Min, H. Nadeau, Mannque Rho, equation (2.20) in: The strangeness problem: An skyrmion with vector mesons, Nuclear Physics A Volume 505, Issues 3–4, 25 December 1989, Pages 497-524 (doi:10.1016/0375-9474(89)90029-8)
specifically D-mesons:
(…)
specifically B-mesons:
- Mannque Rho, D. O. Riska, N. N. Scoccola, above (2.1) in: The energy levels of the heavy flavour baryons in the topological soliton model, Zeitschrift für Physik A Hadrons and Nuclei volume 341, pages343–352 (1992) (doi:10.1007/BF01283544)
Including heavy vector mesons
Inclusion of heavy vector mesons:
specifically K*-mesons:
- S. Ozaki, H. Nagahiro, Atsushi Hosaka, Equations (3) and (9) in: Magnetic interaction induced by the anomaly in kaon-photoproductions, Physics Letters B Volume 665, Issue 4, 24 July 2008, Pages 178-181 (arXiv:0710.5581, doi:10.1016/j.physletb.2008.06.020)
Including electroweak interactions
Including electroweak fields:
-
J. Bijnens, G. Ecker, A. Picha, The chiral anomaly in non-leptonic weak interactions, Physics Letters B Volume 286, Issues 3–4, 30 July 1992, Pages 341-347 (doi:10.1016/0370-2693(92)91785-8)
-
Gerhard Ecker, Helmut Neufeld, Antonio Pich, Non-leptonic kaon decays and the chiral anomaly, Nuclear Physics B Volume 413, Issues 1–2, 31 January 1994, Pages 321-352 (doi:10.1016/0550-3213(94)90623-8)
Discussion for the full standard model of particle physics:
- Jeffrey Harvey, Christopher T. Hill, Richard J. Hill, Standard Model Gauging of the WZW Term: Anomalies, Global Currents and pseudo-Chern-Simons Interactions, Phys. Rev. D77:085017, 2008 (arXiv:0712.1230)
Baryon chiral perturbation theory
Discussion of baryon chiral perturbation theory, i.e of chiral perturbation theory with explicit effective (as opposed to or in addition to implicit skyrmionic) baryon fields included (see also Walecka model and quantum hadrodynamics):
Review:
-
Ulf-G. Meissner, Chiral QCD: Baryon dynamics, in: At The Frontier of Particle Physics, pp. 417-505 (2001) (arxiv:hep-ph/0007092)
-
Véronique Bernard, Chiral Perturbation Theory and Baryon Properties, Prog. Part. Nucl. Phys. 60:82-160, 2008 (arXiv:0706.0312)
-
Stefan Scherer, Baryon chiral perturbation theory, PoS CD09:075, 2009 (arXiv:0910.0331)
Original articles:
-
Elizabeth Jenkins, Aneesh V. Manohar, Baryon chiral perturbation theory using a heavy fermion lagrangian, Physics Letters B Volume 255, Issue 4, 21 February 1991, Pages 558-562 (doi:10.1016/0370-2693(91)90266-S)
-
Robert Baur, Joachim Kambor, Generalized Heavy Baryon Chiral Perturbation Theory, Eur. Phys. J. C7:507-524, 1999 (arXiv:hep-ph/9803311)
Higher order terms:
-
José Antonio Oller, Michela Verbeni, Joaquim Prades, Meson-baryon effective chiral Lagrangians to , Journal of High Energy Physics, Volume 2006, JHEP09(2006) (arXiv:hep-ph/0608204, doi:10.1088/1126-6708/2006/09/079)
-
Matthias Frink, Ulf-G. Meissner, On the chiral effective meson-baryon Lagrangian at third order, Eur. Phys. J. A29:255-260, 2006 (arXiv:hep-ph/0609256)
-
Jose Antonio Oller, Joaquim Prades, Michela Verbeni, Meson-Baryon Effective Chiral Lagrangians at Revisited (arXiv:hep-ph/0701096, spire:742291)
See also:
- Lisheng Geng, Recent developments in covariant baryon chiral perturbation theory, Front. Phys., 2013, 8(3): 328-348 (arXiv:1301.6815)
Applications to lattice QCD
Application to lattice QCD:
- S.R.Sharpe, Applications of Chiral Perturbation theory to lattice QCD, ILFTN Workshop on “Perspectives in Lattice QCD”, Nara, Japan, Oct 31-Nov 11 2005, 2006 (arXiv:hep-lat/0607016)
Inclusion of leptons
On chiral perturbation theory including leptons:
-
M. Knecht, Helmut Neufeld, H. Rupertsberger, P. Talavera, Chiral Perturbation Theory with Virtual Photons and Leptons, Eur. Phys. J. C12:469-478, 2000 (arXiv:hep-ph/9909284)
-
Helmut Neufeld, Chiral Perturbation Theory with Photons and Leptons, PiN Newslett. 15:189-192, 1999 (arXiv:hep-ph/9912462)
Specifically in relation to the Skyrme model:
- Eric D'Hoker, Edward Farhi, The decay of the skyrmion, Physics Letters B Volume 134, Issues 1–2, 5 January 1984, Pages 86-90 (doi:10.1016/0370-2693(84)90991-2)
Antisymmetric tensor representation for vector mesons
The formulation of vector mesons in “antisymmetric tensor representation”:
Original articles:
-
Jürg Gasser, Heinrich Leutwyler, Appendix C of: Chiral perturbation theory to one loop, Annals of Physics Volume 158, Issue 1, November 1984, Pages 142-210 (doi:10.1016/0003-4916(84)90242-2)
-
Gerhard Ecker, Jürg Gasser, Antonio Pich, E. DeRafael, Sec 3 and Appendix A in: The role of resonances in chiral perturbation theory, Nuclear Physics B
Volume 321, Issue 2, 24 July 1989, Pages 311-342 (doi:10.1016/0550-3213(89)90346-5)
Relation between the vector- and the antisymmetric tensor-representation of vector mesons:
- Karol Kampf, Jiri Novotny, Jaroslav Trnka, On different lagrangian formalisms for vector resonances within chiral perturbation theory, Eur. Phys. J. C50:385-403, 2007 (arXiv:hep-ph/0608051)
See also
- V. Dmitrašinović, around (11) in: Axial baryon number nonconserving antisymmetric tensor four-quark effective interaction, Phys. Rev. D 62, 096010 (2000) (doi:10.1103/PhysRevD.62.096010)
Further application of the antisymmetric tensor representation of vector mesons to quantum hadrodynamics:
-
Stefan Leupold, Carla Terschlusen, Towards an effective field theory for vector mesons, Talk presented at the 50th International Winter Meeting on Nuclear Physics, 23-27 January 2012, Bormio (arXiv:1206.2253)
-
Carla Terschlusen, Stefan Leupold, M. F. M. Lutz, Electromagnetic transitions in an effective chiral Lagrangian with the eta-prime and light vector mesons, Eur. Phys. J. A 48, 190 (2012) (arXiv:1204.4125)
Last revised on August 12, 2025 at 21:33:19. See the history of this page for a list of all contributions to it.