nLab hidden local symmetry
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
In the effective field theory sigma-models for Goldstone bosons (such as mesons in chiral perturbation theory of QCD) the global symmetry (e.g. chiral symmetry) may typically be enhanced to a “hidden” local gauge symmetry that exhibits the source vector fields (notably: vector mesons) as gauge fields of a (flavour) gauge theory.
In chiral perturbation theory, the gauge bosons of the hidden local chiral symmetry are identified with the vector mesons. The minimal coupling of these two the baryons yields the vector meson dominance-model of quantum hadrodynamics.
In intersecting D-brane models, such as in holographic QCD, this is geometrically brought out by open strings ending on “flavor branes” instead of “color branes”.
| color charge | flavor charge | |
|---|---|---|
| gauge bosons | gluons (gauge group-local symmetry) | mesons (flavor-hidden local symmetry) |
| fermions | quarks | baryons |
Properties
Relation to Skyrmions
- Dmitri Diakonov, Victor Petrov, Exotic baryon resonances in the Skyrme model (arXiv:0812.1212, doi:10.1142/9789814704410_0004), Chapter 3 in: The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
It is astounding that Skyrme had suggested his model as early as in 1961 before it has been generally accepted that pions are (pseudo) Goldstone bosons associated with the spontaneous breaking of chiral symmetry, and of course long before Quantum Chromodynamics (QCD) has been put forward as the microscopic theory of strong interactions.
The revival of the Skyrme idea in 1983 is due to Witten who explained the raison d’ˆetre of the Skyrme model from the viewpoint of QCD. In the chiral limit when the light quark masses , , tend to zero, such that the octet of the pseudoscalar mesons π, K , η become nearly massless (pseudo) Goldstone bosons, they are the lightest degrees of freedom of QCD. The effective chiral Lagrangian (EχL) for pseudoscalar mesons, understood as an infinite expansion in the derivatives of the pseudoscalar (or chiral) fields, encodes, in principle, full information about QCD. The famous two-term Skyrme Lagrangian can be understood as a low-energy truncation of this infinite series. Witten has added an important four-derivative Wess–Zumino term to the original Skyrme Lagrangian and pointed out that the overall coefficient in front of the EχL is proportional to the number of quark colours .
Soon after Witten’s work it has been realized that it is possible to bring the Skyrme model and the Skyrmion even closer to QCD and to the more customary language of constituent quarks. It has been first noticed 6, 7a, 7b, 8 that a simple chiral invariant Lagrangian for massive (constituent) quarks interacting with the octet chiral field ,
induces, via a quark loop in the external pseudoscalar fields (see Fig. 3.1), the EχL whose lowest-derivative terms coincide with the Skyrme Lagrangian, including automatically the Wess–Zumino term, with the correct coefficient!
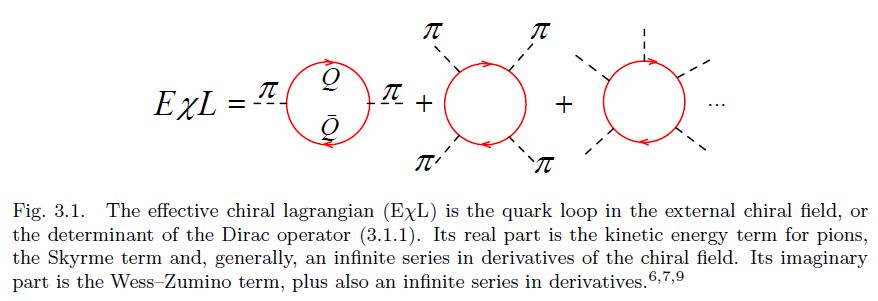
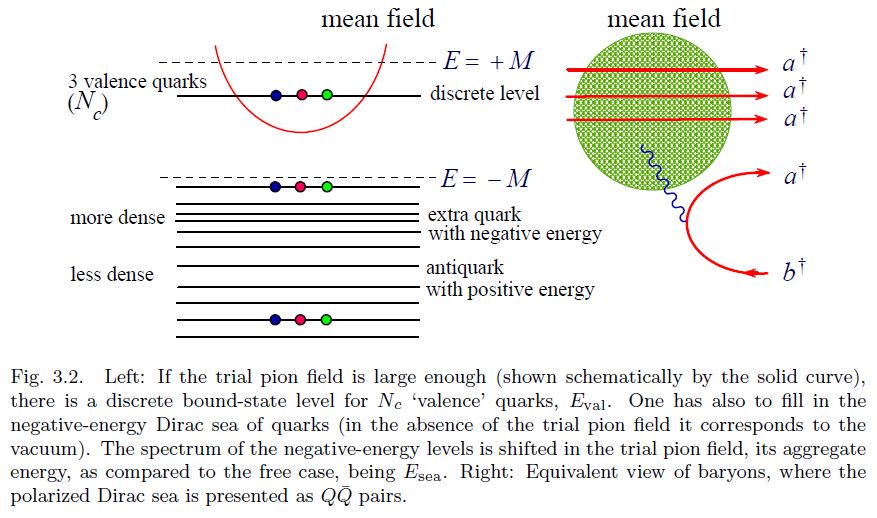
The condition that the winding number of the trial field is unity needs to be imposed to get a deeply bound state, that is to guarantee that the baryon number is unity. 9 The Skyrmion is, thus, nothing but the mean chiral field binding quarks in a baryon.
-
Dmitri Diakonov, Michael I. Eides, Chiral Lagrangian from a functional integral over quarks, JETP Letters 38.7 (1983): 433-436 (pdf, pdf)
-
A. Dhar, Spenta R. Wadia, Nambu—Jona-Lasinio Model: An Effective Lagrangian for Quantum Chromodynamics at Intermediate Length Scales, Phys. Rev. Lett. 52, 959 (1984) (doi:10.1103/PhysRevLett.52.959)
-
Avinash Dhar, R. Shankar, Spenta R. Wadia, Nambu–Jona-Lasinio–type effective Lagrangian: Anomalies and nonlinear Lagrangian of low-energy, large-N QCD, Phys. Rev. D 31, 3256 (1985) (doi:10.1103/PhysRevD.31.3256)
-
Dmitri Diakonov, Victor Petrov, A theory of light quarks in the instanton vacuum, Nuclear Physics B Volume 272, Issue 2, 21 July 1986, Pages 457-489 (doi:10.1016/0550-3213(86)90011-8)
-
Dmitri Diakonov, Victor Petrov, P.V. Pobylitsa, A Chiral Theory of Nucleons, Nucl. Phys. B306 (1988) 809 (spire:247700, doi:10.1016/0550-3213(88)90443-9)
Related concepts
effective field theories of nuclear physics, hence for confined-phase quantum chromodynamics:
References
General
Origin of effective field theory of mesons in nuclear physics, via hidden local gauge symmetry:
- Jun John Sakurai, Theory of strong interactions, Annals Phys. 11 (1960) 1-48 (spire:3218, doi:10.1016/0003-4916(60)90126-3)
Review:
-
Masako Bando, Taichiro Kugo, Koichi Yamawaki, Nonlinear realization and hidden local symmetries, Physics Reports Volume 164, Issues 4–5, July 1988, Pages 217-314 (doi:10.1016/0370-1573(88)90019-1)
-
Yong-Liang Ma, Masayasu Harada, Section 6 of: Lecture notes on the Skyrme model (arXiv:1604.04850, spire:1448311)
(in relation to Skyrmions)
Further original articles:
-
Masako Bando, Taichiro Kugo, S. Uehara, Koichi Yamawaki, and T. Yanagida, Is the Meson a Dynamical Gauge Boson of Hidden Local Symmetry?, Phys. Rev. Lett. 54, 1215 (1985) (doi:10.1103/PhysRevLett.54.1215)
-
Masako Bando, Takanori Fujiwara, Koichi Yamawaki, Generalized Hidden Local Symmetry and the Meson, Progress of Theoretical Physics, Volume 79, Issue 5, May 1988, Pages 1140–1166 (doi:10.1143/PTP.79.1140)
-
Howard Georgi, Vector realization of chiral symmetry, Nuclear Physics B Volume 331, Issue 2, 12 February 1990, Pages 311-330 (doi:10.1016/0550-3213(90)90210-5)
Equivalence between hidden local symmetry- and massive Yang-Mills theory-description of Skyrmion quantum hadrodynamics:
- Atsushi Hosaka, H. Toki, W. Weise, Skyrme Solitons With Vector Mesons: Equivalence of the Massive Yang-Mills and Hidden Local Symmetry Scheme, 1988, Z. Phys. A332 (1989) 97-102 (spire:24079)
In view of the chiral anomaly WZW term:
- Michio Hashimoto, Hidden Local Symmetry for Anomalous Processes with Isospin/ Breaking Effects, Phys. Rev. D54 (1996) 5611-5619 (arXiv:hep-ph/9605422)
With emphasis on Skyrmions involving vector mesons:
-
Yong-Liang Ma, Ghil-Seok Yang, Yongseok Oh, Masayasu Harada, Skyrmions with vector mesons in the hidden local symmetry approach, Phys. Rev. D87:034023, 2013 (arXiv:1209.3554)
-
Mannque Rho, Skyrmions and Fractional Quantum Hall Droplets Unified by Hidden Symmetries in Dense Matter (arXiv:2109.10059)
Hadrons as KK-modes of 5d Yang-Mills theory
The suggestion that the tower of observed vector mesons – when regarded as gauge fields of hidden local symmetries of chiral perturbation theory – is reasonably modeled as a Kaluza-Klein tower of D=5 Yang-Mills theory:
- D. T. Son, M. A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182, doi:10.1103/PhysRevD.69.065020)
That the pure pion-Skyrmion-model of baryons is approximately the KK-reduction of instantons in D=5 Yang-Mills theory is already due to:
- Michael Atiyah, Nicholas Manton, Skyrmions from instantons, Phys. Lett. B, 222(3):438–442, 1989 (doi:10.1016/0370-2693(89)90340-7)
with a hyperbolic space-variant in:
- Michael Atiyah, Paul Sutcliffe, Skyrmions, instantons, mass and curvature, Phys. Lett. B605 (2005) 106-114 (arXiv:hep-th/0411052)
Further discussion of this approximation:
- Josh Cork, Chris Halcrow, ADHM skyrmions (arXiv:2110.15190)
The observation that the result of Atiyah-Manton 89 becomes an exact Kaluza-Klein construction of Skyrmions/baryons from D=5 instantons when the full KK-tower of vector mesons as in Son-Stephanov 03 is included into the Skyrmion model (see also there) is due to:
-
Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
-
Paul Sutcliffe, Holographic Skyrmions, Mod. Phys. Lett. B29 (2015) no. 16, 1540051 (spire:1383608, doi:10.1142/S0217984915400515)
In the Sakai-Sugimoto model of holographic QCD the D=5 Yang-Mills theory of this hadron Kaluza-Klein theory is identified with the worldvolume-theory of D8-flavour branes intersected with D4-branes in an intersecting D-brane model:
-
Tadakatsu Sakai, Shigeki Sugimoto, section 5.2 of Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, section 3.3. of More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)
-
Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, Shinichiro Yamato, Baryons from instantons in holographic QCD, Prog.Theor.Phys.117:1157, 2007 (arXiv:hep-th/0701280)
-
Stefano Bolognesi, Paul Sutcliffe, The Sakai-Sugimoto soliton, JHEP 1401:078, 2014 (arXiv:1309.1396)
-
Lorenzo Bartolini, Stefano Bolognesi, Andrea Proto, From the Sakai-Sugimoto Model to the Generalized Skyrme Model, Phys. Rev. D 97 014024 (2018) [doi:10.1103/PhysRevD.97.014024, arXiv:1711.03873]
-
Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Tommaso Rainaldi, Mass and Isospin Breaking Effects in the Skyrme Model and in Holographic QCD [arXiv:2312.15404]
Extensive review of this holographic/KK-theoretic-realization of quantum hadrodynamics from D=5 Yang-Mills theory is in:
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific, Second edition, 2016 (doi:10.1142/9710)
- Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Via the realization of D4/D8 brane bound states as instantons in the D8-brane worldvolume-theory (see there and there), this relates also to the model of baryons as wrapped D4-branes, originally due to
-
Edward Witten, Baryons And Branes In Anti de Sitter Space, JHEP 9807:006, 1998 (arXiv:hep-th/9805112)
-
David Gross, Hirosi Ooguri, Aspects of Large Gauge Theory Dynamics as Seen by String Theory, Phys. Rev. D58:106002, 1998 (arXiv:hep-th/9805129)
and further developed in the nuclear matrix model:
-
Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
In relation to Yang-Mills monopoles:
- Stefano Bolognesi, Solitons, Large and Holography, 2015 (pdf)
Discussion, in this context, of D-term effects affecting hadron stability:
- Mitsutoshi Fujita, Yoshitaka Hatta, Shigeki Sugimoto, Takahiro Ueda, Nucleon D-term in holographic QCD arXiv:2206.06578
More on baryons in the Sakai-Sugimoto model of holographic QCD:
- Salvatore Baldino, Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Holographic Nuclear Physics with Massive Quarks, Phys. Rev. D 103 126015 (2021) [doi:10.1103/PhysRevD.103.126015, arXiv:2102.00680]
More on mesons in holographic QCD:
-
Johanna Erdmenger, Nick Evans, Ingo Kirsch, Ed Threlfall, Mesons in Gauge/Gravity Duals - A Review, Eur. Phys. J. A 35 (2008) 81-133 [arXiv:0711.4467, doi:10.1140/epja/i2007-10540-1]
-
Daniel Ávila, Leonardo Patiño, Melting holographic mesons by cooling a magnetized quark gluon plasma (arXiv:2002.02470)
-
Xuanmin Cao, Hui Liu, Danning Li, Pion quasiparticles and QCD phase transitions at finite temperature and isospin density from holography, Phys. Rev. D 102, 126014 (2020) (arXiv:2009.00289)
-
Xuanmin Cao, Songyu Qiu, Hui Liu, Danning Li, Thermal properties of light mesons from holography (arXiv:2102.10946)
-
Artur Amorim, Miguel S. Costa, Matti Järvinen, Regge theory in a Holographic dual of QCD in the Veneziano Limit (arXiv:2102.11296)
-
Roldão da Rocha, Information in AdS/QCD: mass spectroscopy of isovector mesons, Phys. Rev. D 103 106027 (2021) [arXiv:2103.03924, doi:10.1103/PhysRevD.103.106027]
-
Shahin Mamedov, Narmin Nasibova, Temperature dependence of meson-nucleon coupling constant from the soft-wall model (arXiv:2103.10494)
An alternative scenario of derivation of 4d Skyrmions by KK-compactification of D=5 Yang-Mills theory, now on a closed interval, motivated by M5-branes instead of by D4/D8-brane intersections as in the Sakai-Sugimoto model, is discussed in:
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Skyrme model from 6d theory, Physics Letters B 783 (2018), 222-226 [doi:10.1016/j.physletb.2018.06.052, arXiv:1805.07241]
with related discussion in:
-
Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Non-Abelian sigma models from Yang-Mills theory compactified on a circle, Physics Letters B 781 (2018) 322-326 [doi:10.1016/j.physletb.2018.04.013arXiv:1803.07322]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme-Faddeev model from 5d super-Yang-Mills, Phys. Lett. B 786 (2018) 39-44 [doi:10.1016/j.physletb.2018.09.028, arXiv:1807.11803]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme and Faddeev models in the low-energy limit of 4d Yang-Mills-Higgs theories, Nuclear Physics B 945 (2019) 114675 [doi:10.1016/j.nuclphysb.2019.114675, arXiv:1808.08972]
See also:
- Y. H. Ahn, Sin Kyu Kang, Hyun Min Lee, Towards a Model of Quarks and Leptons (arXiv:2112.13392)
In D-brane models
Further interpretation/derivation of hidden local symmetry in holographic QCD:
-
D. T. Son, M. A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182, doi:10.1103/PhysRevD.69.065020)
(also derivation of vector meson dominance)
-
Masayasu Harada, Shinya Matsuzaki, and Koichi Yamawaki, Implications of holographic QCD in chiral perturbation theory with hidden local symmetry, Phys. Rev. D 74, 076004 (2006) (doi:10.1103/PhysRevD.74.076004)
(on small N corrections to holographic QCD)
-
Hyun Kyu Lee, Mannque Rho, Section 6.2.1 of: Half-Skyrmion Hadronic Matter at High Density (doi:10.1142/9789814280709_0006), Chapter 6 in: Mannque Rho et al., The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Last revised on October 6, 2021 at 12:28:38. See the history of this page for a list of all contributions to it.