nLab baryon
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
In the standard model of particle physics (specifically in QCD), a baryon is bound state of three quarks via the strong nuclear force. Baryons are the “heavy” types of hadrons, the other being the mesons.
Examples of baryons are the nucleons: protons and neutrons. Other examples are Lambda baryons.
Also pentaquarks are counted as baryons.
Properties
Conceptualization and computation in AdS/QCD
In the Witten-Sakai-Sugimoto model for strongly coupled QCD via an intersecting D-brane model, the hadrons in QCD correspond to string-theoretic-phenomena in an ambient bulk field theory on an approximately anti de Sitter spacetime:
-
the mesons (bound states of 2 quarks) correspond to open strings in the bulk, whose two endpoints on the asymptotic boundary correspond to the two quarks;
-
baryons (bound states of quarks) appear in two different but equivalent (Sugimoto 16, 15.4.1) guises:
-
as wrapped D4-branes with open strings connecting them to the D8-brane
-
as skyrmions
(Sakai-Sugimoto 04, section 5.2, Sakai-Sugimoto 05, section 3.3, see Bartolini 17).
-
For review see Sugimoto 16, also Rebhan 14, around (18).
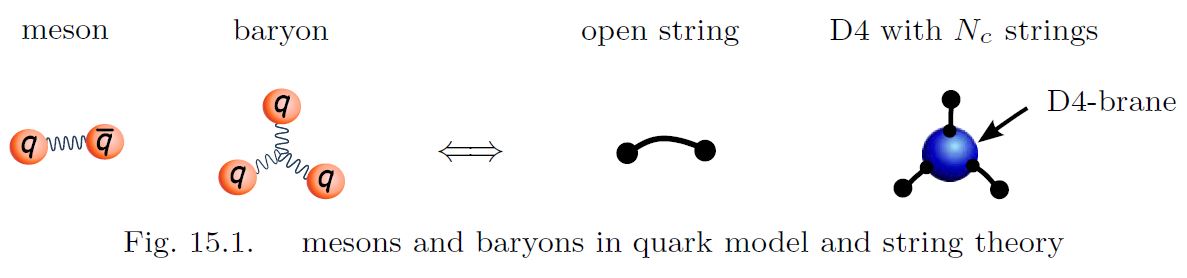
graphics grabbed from Sugimoto 16
This produces baryon mass spectra with moderate quantitative agreement with experiment (HSSY 07):
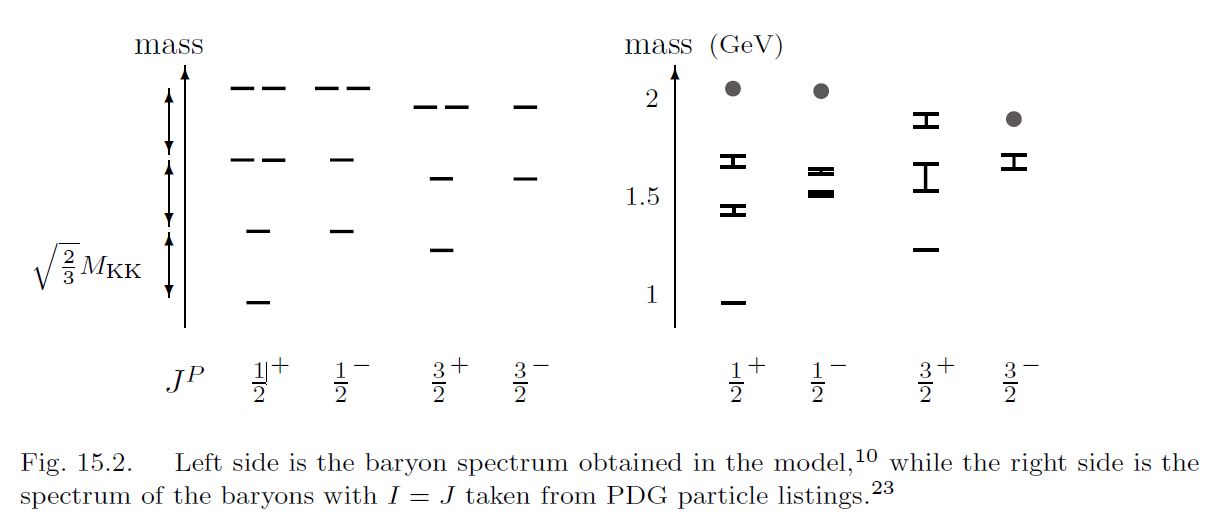
graphics grabbed from Sugimoto 16
Related concepts
References
General
Introduction and review:
- Franz Gross, Eberhard Klempt et al., Chapter 9 of: 50 Years of Quantum Chromodynamics, EJPC [arXiv:2212.11107]
Baryons as 3-constituent quark bound states:
- Gernot Eichmann, Helios Sanchis-Alepuz, Richard Williams, Reinhard Alkofer, Christian S. Fischer, Baryons as relativistic three-quark bound states, Progress in Particle and Nuclear Physics Volume 91, November 2016, Pages 1-100 (arXiv:1606.09602, doi:10.1016/j.ppnp.2016.07.001)
Baryons as quark/diquark bound states:
- Martin Oettel, Baryons as Relativistic Bound States of Quark and Diquark (arXiv:nucl-th/0012067, spire:538966)
Experiment:
- Eberhard Klempt, Jean-Marc Richard, Baryon spectroscopy, Rev. Mod. Phys. 82:1095-1153, 2010 (arXiv:0901.2055
See also
Baryon chiral perturbation theory
Discussion of baryon chiral perturbation theory, i.e of chiral perturbation theory with explicit effective (as opposed to or in addition to implicit skyrmionic) baryon fields included (see also Walecka model and quantum hadrodynamics):
Review:
-
Ulf-G. Meissner, Chiral QCD: Baryon dynamics, in: At The Frontier of Particle Physics, pp. 417-505 (2001) (arxiv:hep-ph/0007092)
-
Véronique Bernard, Chiral Perturbation Theory and Baryon Properties, Prog. Part. Nucl. Phys. 60:82-160, 2008 (arXiv:0706.0312)
-
Stefan Scherer, Baryon chiral perturbation theory, PoS CD09:075, 2009 (arXiv:0910.0331)
Original articles:
-
Elizabeth Jenkins, Aneesh V. Manohar, Baryon chiral perturbation theory using a heavy fermion lagrangian, Physics Letters B Volume 255, Issue 4, 21 February 1991, Pages 558-562 (doi:10.1016/0370-2693(91)90266-S)
-
Robert Baur, Joachim Kambor, Generalized Heavy Baryon Chiral Perturbation Theory, Eur. Phys. J. C7:507-524, 1999 (arXiv:hep-ph/9803311)
Higher order terms:
-
José Antonio Oller, Michela Verbeni, Joaquim Prades, Meson-baryon effective chiral Lagrangians to , Journal of High Energy Physics, Volume 2006, JHEP09(2006) (arXiv:hep-ph/0608204, doi:10.1088/1126-6708/2006/09/079)
-
Matthias Frink, Ulf-G. Meissner, On the chiral effective meson-baryon Lagrangian at third order, Eur. Phys. J. A29:255-260, 2006 (arXiv:hep-ph/0609256)
-
Jose Antonio Oller, Joaquim Prades, Michela Verbeni, Meson-Baryon Effective Chiral Lagrangians at Revisited (arXiv:hep-ph/0701096, spire:742291)
See also:
- Lisheng Geng, Recent developments in covariant baryon chiral perturbation theory, Front. Phys., 2013, 8(3): 328-348 (arXiv:1301.6815)
Baryons as Skyrmions
The Skyrmion-model for baryons (see there for more references):
-
Herbert Weigel, Baryons as Three Flavor Solitons, Int. J. Mod. Phys. A11:2419-2544, 1996 (arXiv:hep-ph/9509398, cds:288541, doi:10.1142/S0217751X96001218)
-
Herbert Weigel, Chiral Soliton Models for Baryons, Lecture Notes in Physics book series, volume 743, Springer 2008 (doi:10.1007/978-3-540-75436-7)
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Hadrons as KK-modes of 5d Yang-Mills theory
The suggestion that the tower of observed vector mesons – when regarded as gauge fields of hidden local symmetries of chiral perturbation theory – is reasonably modeled as a Kaluza-Klein tower of D=5 Yang-Mills theory:
- D. T. Son, M. A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182, doi:10.1103/PhysRevD.69.065020)
That the pure pion-Skyrmion-model of baryons is approximately the KK-reduction of instantons in D=5 Yang-Mills theory is already due to:
- Michael Atiyah, Nicholas Manton, Skyrmions from instantons, Phys. Lett. B, 222(3):438–442, 1989 (doi:10.1016/0370-2693(89)90340-7)
with a hyperbolic space-variant in:
- Michael Atiyah, Paul Sutcliffe, Skyrmions, instantons, mass and curvature, Phys. Lett. B605 (2005) 106-114 (arXiv:hep-th/0411052)
Further discussion of this approximation:
- Josh Cork, Chris Halcrow, ADHM skyrmions (arXiv:2110.15190)
The observation that the result of Atiyah-Manton 89 becomes an exact Kaluza-Klein construction of Skyrmions/baryons from D=5 instantons when the full KK-tower of vector mesons as in Son-Stephanov 03 is included into the Skyrmion model (see also there) is due to:
-
Paul Sutcliffe, Skyrmions, instantons and holography, JHEP 1008:019, 2010 (arXiv:1003.0023)
-
Paul Sutcliffe, Holographic Skyrmions, Mod. Phys. Lett. B29 (2015) no. 16, 1540051 (spire:1383608, doi:10.1142/S0217984915400515)
In the Sakai-Sugimoto model of holographic QCD the D=5 Yang-Mills theory of this hadron Kaluza-Klein theory is identified with the worldvolume-theory of D8-flavour branes intersected with D4-branes in an intersecting D-brane model:
-
Tadakatsu Sakai, Shigeki Sugimoto, section 5.2 of Low energy hadron physics in holographic QCD, Prog.Theor.Phys.113:843-882, 2005 (arXiv:hep-th/0412141)
-
Tadakatsu Sakai, Shigeki Sugimoto, section 3.3. of More on a holographic dual of QCD, Prog.Theor.Phys.114:1083-1118, 2005 (arXiv:hep-th/0507073)
-
Hiroyuki Hata, Tadakatsu Sakai, Shigeki Sugimoto, Shinichiro Yamato, Baryons from instantons in holographic QCD, Prog.Theor.Phys.117:1157, 2007 (arXiv:hep-th/0701280)
-
Stefano Bolognesi, Paul Sutcliffe, The Sakai-Sugimoto soliton, JHEP 1401:078, 2014 (arXiv:1309.1396)
-
Lorenzo Bartolini, Stefano Bolognesi, Andrea Proto, From the Sakai-Sugimoto Model to the Generalized Skyrme Model, Phys. Rev. D 97 014024 (2018) [doi:10.1103/PhysRevD.97.014024, arXiv:1711.03873]
-
Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Tommaso Rainaldi, Mass and Isospin Breaking Effects in the Skyrme Model and in Holographic QCD [arXiv:2312.15404]
Extensive review of this holographic/KK-theoretic-realization of quantum hadrodynamics from D=5 Yang-Mills theory is in:
-
Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific, Second edition, 2016 (doi:10.1142/9710)
- Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
Via the realization of D4/D8 brane bound states as instantons in the D8-brane worldvolume-theory (see there and there), this relates also to the model of baryons as wrapped D4-branes, originally due to
-
Edward Witten, Baryons And Branes In Anti de Sitter Space, JHEP 9807:006, 1998 (arXiv:hep-th/9805112)
-
David Gross, Hirosi Ooguri, Aspects of Large Gauge Theory Dynamics as Seen by String Theory, Phys. Rev. D58:106002, 1998 (arXiv:hep-th/9805129)
and further developed in the nuclear matrix model:
-
Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
In relation to Yang-Mills monopoles:
- Stefano Bolognesi, Solitons, Large and Holography, 2015 (pdf)
Discussion, in this context, of D-term effects affecting hadron stability:
- Mitsutoshi Fujita, Yoshitaka Hatta, Shigeki Sugimoto, Takahiro Ueda, Nucleon D-term in holographic QCD arXiv:2206.06578
More on baryons in the Sakai-Sugimoto model of holographic QCD:
- Salvatore Baldino, Lorenzo Bartolini, Stefano Bolognesi, Sven Bjarke Gudnason, Holographic Nuclear Physics with Massive Quarks, Phys. Rev. D 103 126015 (2021) [doi:10.1103/PhysRevD.103.126015, arXiv:2102.00680]
More on mesons in holographic QCD:
-
Johanna Erdmenger, Nick Evans, Ingo Kirsch, Ed Threlfall, Mesons in Gauge/Gravity Duals - A Review, Eur. Phys. J. A 35 (2008) 81-133 [arXiv:0711.4467, doi:10.1140/epja/i2007-10540-1]
-
Daniel Ávila, Leonardo Patiño, Melting holographic mesons by cooling a magnetized quark gluon plasma (arXiv:2002.02470)
-
Xuanmin Cao, Hui Liu, Danning Li, Pion quasiparticles and QCD phase transitions at finite temperature and isospin density from holography, Phys. Rev. D 102, 126014 (2020) (arXiv:2009.00289)
-
Xuanmin Cao, Songyu Qiu, Hui Liu, Danning Li, Thermal properties of light mesons from holography (arXiv:2102.10946)
-
Artur Amorim, Miguel S. Costa, Matti Järvinen, Regge theory in a Holographic dual of QCD in the Veneziano Limit (arXiv:2102.11296)
-
Roldão da Rocha, Information in AdS/QCD: mass spectroscopy of isovector mesons, Phys. Rev. D 103 106027 (2021) [arXiv:2103.03924, doi:10.1103/PhysRevD.103.106027]
-
Shahin Mamedov, Narmin Nasibova, Temperature dependence of meson-nucleon coupling constant from the soft-wall model (arXiv:2103.10494)
An alternative scenario of derivation of 4d Skyrmions by KK-compactification of D=5 Yang-Mills theory, now on a closed interval, motivated by M5-branes instead of by D4/D8-brane intersections as in the Sakai-Sugimoto model, is discussed in:
- Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Skyrme model from 6d theory, Physics Letters B 783 (2018), 222-226 [doi:10.1016/j.physletb.2018.06.052, arXiv:1805.07241]
with related discussion in:
-
Tatiana Ivanova, Olaf Lechtenfeld, Alexander Popov, Non-Abelian sigma models from Yang-Mills theory compactified on a circle, Physics Letters B 781 (2018) 322-326 [doi:10.1016/j.physletb.2018.04.013arXiv:1803.07322]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme-Faddeev model from 5d super-Yang-Mills, Phys. Lett. B 786 (2018) 39-44 [doi:10.1016/j.physletb.2018.09.028, arXiv:1807.11803]
-
Olaf Lechtenfeld, Alexander D. Popov, Skyrme and Faddeev models in the low-energy limit of 4d Yang-Mills-Higgs theories, Nuclear Physics B 945 (2019) 114675 [doi:10.1016/j.nuclphysb.2019.114675, arXiv:1808.08972]
See also:
- Y. H. Ahn, Sin Kyu Kang, Hyun Min Lee, Towards a Model of Quarks and Leptons (arXiv:2112.13392)
In the large limit
In the large N limit:
- Edward Witten, Baryons in the Expansion, Nucl. Phys. B160 (1979) 57-115 (spire:140391, doi:10.1016/0550-3213(79)90232-3)
Last revised on December 22, 2022 at 03:25:54. See the history of this page for a list of all contributions to it.