nLab confinement
Context
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Differential cohomology
Ingredients
Connections on bundles
Higher abelian differential cohomology
Higher nonabelian differential cohomology
Fiber integration
Application to gauge theory
Contents
Idea
Confinement (e.g Espiru 94) is the (expected) phenomenon in Yang-Mills theory generally and especially in quantum chromodynamics that the fundamental quarks, which the YM/QCD-Lagrangian density actually describes, must form baryonic bound states which are neutral under the color charge – the mesons and hadrons (protons, neutrons). Hence confinement in particular concerns the emergence and existence of atomic nuclei, hence of ordinary matter, which is not manifest at all in the quark-model. In order to prove, via QCD itself, that the potential energy of a colorless package of quarks tends to infinity as the distance between them grows, one must probe the long-range regime of the quark-quark interaction, in which the methods of Feynman perturbation theory fail.
Part of the issue is that confinement is a non-perturbative effect (e.g Espiru 94) outside the range of validity of perturbative quantum field theory.
The open problem of confinement
While experiment as well as lattice gauge theory-computer simulation clearly show that confinement takes place, a real theoretical understanding has been missing (though AdS-QCD is now on a good track). This is the confinement problem. The same problem from the point of view of mathematics is called the Yang-Mills mass gap Millennium Problem. A related problem is the flavor problem.
The following is a list of quotes highlighting the open problem of confinement:
- Edward Witten, Baryons in the Expansion, Nucl. Phys. B160 (1979) 57-115 (spire:140391, doi:10.1016/0550-3213(79)90232-3)
many of the essential properties that the theory QCD is presumed to have, including confinement, dynamical mass generation, and chiral symmetry breaking, are only poorly understood. And apart from the low-lying bound states of heavy quarks, which we believe can be described by a nonrelativistic Schroedinger equation, we are unable to derive from the basic theory even the grossest features of the particle spectrum, or of traditional strong interaction phenomenology
- Rupert Machleidt, The Meson Theory of Nuclear Forces and Nuclear Structure, In: Negele J.W., Vogt E. (eds.) Advances in Nuclear Physics Advances in Nuclear Physics, vol 19. Springer 1989 (doi:10.1007/978-1-4613-9907-0_2)
There are theoretical attempts to connect the fundamental theory of QCD with the very successful meson picture at low energy. The Skyrme model is an example. In other attempts, one tries to derive the NN interaction more or less directly from QCD. At present, the predictions are more of a qualitative kind. For quantitative results, the one-pion and two-pion contributions have to be added by hand, as they do not emerge naturally out of QCD-inspired models. Knowing that and are the most important parts of the nuclear force, this defect of present quark model calculations is serious.
- Robert Kutschke, section 3.1 Heavy flavour spectroscopy, in D. Bugg (ed.), Hadron Spectroscopy and the Confinement Problem, Proceedings of a NATO Advanced Study Institute, Plenum Press 1996 (doi:10.1007/978-1-4613-0375-6)
While it is generally believed that QCD is the correct fundamental theory of the strong interactions there are, as yet, no practical means to produce full QCD calculations of hadron masses and their decay widths.
- Barry R. Holstein, A Brief Introduction to Chiral Perturbation Theory, Czech. J. Phys. 50S4:9-23, 2000 (arXiv:hep-ph/9911449)
the holy grail sought by particle/nuclear knights has been to verify the correctness of the “ultimate” theory of strong interactions – quantum chromodynamics (QCD).
The theory is, of course, deceptively simple on the surface. So why are we still not satisfied? While at the very largest energies, asymptotic freedom allows the use of perturbative techniques, for those who are interested in making contact with low energy experimental findings there exist at least three fundamental difficulties:
i) QCD is written in terms of the “wrong” degrees of freedom – quarks and gluons – while low energy experiments are performed with hadronic bound states;
ii) the theory is non-linear due to gluon self-interactions;
iii) the theory is one of strong coupling so that perturbative methods are not practical
- Igor Klebanov, Oyvind Tafjord, “Can we quantitatively understand quark and gluon confinement in Quantum Chromodynamics and the existence of a mass gap?”, 10th of 10 Physics Problems for the Next Millennium selected at Strings 2000
-
Yakov Shnir, Magnetic Monopoles, Springer 2005 (ISBN:978-3-540-29082-7)
Section 9.1:
confinement still remains one of the very few Big Unsolved Problems of the theoretical physics of the XXI-st century. Moreover, this is the “classic question that has resisted solution over the years”, which was included by the Clay Mathematics Institute in the list of seven Millennium Prize Problems . The award will amount to USD 1,000,000, thus, it is worth-while to account for more information about the matter.
-
Csaba Csaki, Matthew Reece, Toward a Systematic Holographic QCD: A Braneless Approach, JHEP 0705:062, 2007 (arxiv:hep-ph/0608266)
(in motivation of AdS/QCD)
QCD is a perennially problematic theory. Despite its decades of experimental support, the detailed low-energy physics remains beyond our calculational reach. The lattice provides a technique for answering nonperturbative questions, but to date there remain open questions that have not been answered.
-
Mike Guidry, Gauge Field Theories: An Introduction with Applications, Wiley 2008 (ISBN:978-3-527-61736-4)
Section 13.1.9:
The holy grail of QCD is the proof that a color SU(3) gauge theory confines in the non-perturbative regime.
This is not difficult to show for lattices with large spacing; unfortunately, such a demonstration does not constitute a proof of QCD confinement: to do that we must also demonstrate that the same theory that confines at large lattice spacing (strong coupling) has a continuum limit (weak coupling) that is consistent with the asymptotically free short distance behavior of QCD.
- Piljin Yi, Holographic Baryons (arXiv:0902.4515, doi:10.1142/9789814280709_0016), Chapter 16 in: Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)
QCD is a challenging theory. Its most interesting aspects, namely the confinement of color and the chiral symmetry breaking, have defied all analytical approaches. While there are now many data accumulated from the lattice gauge theory, the methodology falls well short of giving us insights on how one may understand these phenomena analytically, nor does it give us a systematic way of obtaining a low energy theory of QCD below the confinement scale.
- Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
Nuclear physics is one of the oldest branches of high energy physics, yet remains one of more difficult. Despite the fact that we know the underlying fundamental theory, i.e. QCD, we are still unable to predict, reliably and analytically, behavior of nuclei or even a single proton. The problem is of course that one must understand the strong-coupling regime of QCD, which by and large remains inaccessible except by large-scale lattice simulations. Traditionally, this sets nuclear physics apart from the rest of high energy physics in many aspects. However, recent developments in the so-called gauge/gravity duality began to solve certain strongly coupled field theories,possibly including QCD or its close relatives, allowing the two communities to merge with each other.
- Jeff Greensite, An Introduction to the Confinement Problem, Lecture Notes in Physics, Volume 821, 2011 (doi:10.1007/978-3-642-14382-3)
Because of the great importance of the standard model, and the central role it plays in our understanding of particle physics, it is unfortunate that, in one very important respect, we don’t really understand how it works. The problem lies in the sector dealing with the interactions of quarks and gluons, the sector known as Quantum Chromodynamics or QCD. We simply do not know for sure why quarks and gluons, which are the fundamental fields of the theory, don’t show up in the actual spectrum of the theory, as asymptotic particle states. There is wide agreement about what must be happening in high energy particle collisions: the formation of color electric flux tubes among quarks and antiquarks, and the eventual fragmentation of those flux tubes into mesons and baryons, rather than free quarks and gluons. But there is no general agreement about why this is happening, and that limitation exposes our general ignorance about the workings of non-abelian gauge theories in general, and QCD in particular, at large distance scales.
- Rupert Machleidt, David Rodríguez Entem, Chiral effective field theory and nuclear forces, Phys. Rept. 503:1-75, 2011 (arXiv:1105.2919, doi:10.1016/j.physrep.2011.02.001)
The problem with a derivation of nuclear forces from QCD is that this theory is non-perturbative in the low-energy regime characteristic of nuclear physics, which makes direct solutions very difficult. Therefore, during the first round of new attempts, QCD-inspired quark models became popular. The positive aspect of these models is that they try to explain hadron structure and hadron-hadron interactions on an equal footing and, indeed, some of the gross features of the nucleon-nucleon interaction are explained successfully.
However, on a critical note, it must be pointed out that these quark-based approaches are nothing but another set of models and, thus, do not represent fundamental progress. For the purpose of describing hadron-hadron interactions, one may equally well stay with the simpler and much more quantitative meson models.
- Koji Hashimoto, D-Brane – Superstrings and New Perspective of Our World, Springer (2012) doi:10.1007/978-3-642-23574-0, spire:1188897
pp 126: Heuristically, one may speculate that, since the coupling constant of QCD is too large, quarks bind together so that any single quark may not be able to exist alone. However, it has never been proved theoretically. After all, at present we have not understood yet QCD, the theory with a large coupling constant in which quantum theoretical effects (many loops in Feynman graphs as in Fig. 2.18) are essential. This is really a serious problem. Actually, one of big seven mathematical millennium problems proposed by Clay mathematical institute in the United States is concerning this QCD, and one million dollars will be awarded for a solution of the problem related with this.
D-branes give us quite an innovative idea, as an approach to this problem. It is called “holography” which is introduced in this chapter.
- Brambilla et al.: QCD and strongly coupled gauge theories - challenges and perspectives, Eur Phys J C Part Fields. 74 10 (2014) 2981 [doi:10.1140/epjc/s10052-014-2981-5, arXiv:1404.3723]
The success of the technique does not remove the challenge of understanding the non-perturbative aspects of the theory. The two aspects are deeply intertwined. The Lagrangian of QCD is written in terms of quark and gluon degrees of freedom which become apparent at large energy but remain hidden inside hadrons in the low-energy regime. This confinement property is related to the increase of at low energy, but it has never been demonstrated analytically.
We have clear indications of the confinement of quarks into hadrons from both experiments and lattice QCD. Computations of the heavy quark–antiquark potential, for example, display a linear behavior in the quark–antiquark distance, which cannot be obtained in pure perturbation theory. Indeed the two main characteristics of QCD: confinement and the appearance of nearly massless pseudoscalar mesons, emergent from the spontaneous breaking of chiral symmetry, are non-perturbative phenomena whose precise understanding continues to be a target of research.
Even in the simpler case of gluodynamics in the absence of quarks, we do not have a precise understanding of how a gap in the spectrum is formed and the glueball spectrum is generated.
- Istituto Nazionale di Fisica Nucleare, What Next: White Paper of the INFN-CSN1 Proposal for a long term strategy for accelerator based experiments, Frascati Phys.Ser. 60 (2015) 1-302 (2015-05-29) (spire:1374543, pdf ) chapter 7: Hadron Physics and non-perturbative QCD (pdf)
Experimentally, there is a large number of facts that lack a detailed qualitative and quantitative explanation. The most spectacular manifestation of our lack of theoretical understanding of QCD is the failure to observe the elementary degrees of freedom, quarks and gluons, as free asymptotic states (color con- finement) and the occurrence, instead, of families of massive mesons and baryons (hadrons) that form approximately linear Regge trajectories in the mass squared. The internal, partonic structure of hadrons, and nucleons in particular, is still largely mysterious. Since protons and neutrons form almost all the visible matter of the Universe, it is of basic importance to explore their static and dynamical properties in terms of quarks and gluons interacting according to QCD dynamics.
- J J Cobos-Martínez, Non-perturbative QCD and hadron physics 2016 J. Phys.: Conf. Ser. 761 012036 (doi:10.1088/1742-6596/761/1/012036)
the QCD Lagrangian does not by itself explain the data on strongly interacting matter, and it is not clear how the observed bound states, the hadrons, and their properties arise from QCD. Neither confinement nor dynamical chiral symmetry breaking (DCSB) is apparent in QCD’s lagrangian, yet they play a dominant role in determining the observable characteristics of QCD. The physics of strongly interacting matter is governed by emergent phenomena such as these, which can only be elucidated through the use of non-perturbative methods in QCD [4, 5, 6, 7]
- Hideo Suganuma, Yuya Nakagawa, Kohei Matsumoto, 1+1 Large QCD and its Holographic Dual -Soliton Picture of Baryons in Single-Flavor World, Proceedings of the 14th International Conference on Meson-Nucleon Physics and the Structure of the Nucleon (MENU2016) (arxiv:1610.02074)
Since 1973, quantum chromodynamics (QCD) has been established as the fundamental theory of the strong interaction. Nevertheless, it is very difficult to solve QCD directly in an analytical manner, and many effective models of QCD have been used instead of QCD, but most models cannot be derived from QCD and its connection to QCD is unclear. To analyze nonperturbative QCD, the lattice QCD Monte Carlo simulation has been also used as a first-principle calculation of the strong interaction. However, it has several weak points. For example, the state information (e.g. the wave function) is severely limited, because lattice QCD is based on the path-integral formalism. Also, it is difficult to take the chiral limit, because zero-mass pions require infinite volume lattices. There appears a notorious “sign problem” at finite density.
On the other hand, holographic QCD has a direct connection to QCD, and can be derived from QCD in some limit. In fact, holographic QCD is equivalent to infrared QCD in large and strong ‘t Hooft coupling , via gauge/gravity correspondence. Remarkably, holographic QCD is successful to reproduce many hadron phenomenology such as vector meson dominance, the KSRF relation, hidden local symmetry, the GSW model and the Skyrme soliton picture. Unlike lattice QCD simulations, holographic QCD is usually formulated in the chiral limit, and does not have the sign problem at finite density.
- V. A. Petrov, Asymptotic Regimes of Hadron Scattering in QCD (arXiv:1901.02628)
This is a commonplace that so far we do not have a full-fledged theory of interaction of hadrons, derived from the first principles of QCD and having a regular way of calculating of hadronic amplitudes, especially at high energies and small momentum transfers. The problem is related to a more general problem that QCD Lagrangian would yield colour confinement with massive colourless physical states (hadrons).
- Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
One of the long-standing problems in QCD is to reproduce profound nuclear physics. The strong coupling nature of QCD prevents us from solving it analytically, and even numerical simulations have a limitation such as the volume of the atomic nucleus versus the lattice size. It is quite important to bridge the particle physics and the nuclear physics, by solving QCD to derive typical fundamental notions of the nuclear physics, such as the magic numbers, the nuclear binding energy and the nuclear shell model.
Holographic QCD is an analytic method to approach these problems in the strong coupling limit and at a large . The nuclear matrix model is a many-body quantum effective mechanics for multiple baryons, derived by the AdS/CFT correspondence applied to QCD.
- Gergely Gábor Barnaföldi, Vakhtang Gogokhia, The Mass Gap Approach to QCD (arXiv:1904.07748)
QCD as a fundamental quantum field gauge theory still suffers from a few important conceptual problems. We focus on some of them as follows: (A) The dynamical generation of a mass squared at the fundamental quark-gluon level, since the QCD Lagrangianforbids such kind of terms apart from the current quark mass. (D) The non-observation of the colored objects as physical states which does not follow from the QCD Lagrangian,i.e., it cannot explain confinement of gluons and quarks.
- Yonggoo Heo, C. Kobdaj, M.F.M. Lutz, Constraints from a large- analysis on meson-baryon interactions at chiral order , Phys. Rev. D 100, 094035 (2019) (arXiv:1908.11816)
Still after many decades of vigorous studies the outstanding challenge of modern physics is to establish a rigorous link of QCD to low-energy hadron physics as it is observed in the many experimental cross section measurements.
- Christian Drischler, Wick Haxton, Kenneth McElvain, Emanuele Mereghetti, Amy Nicholson, Pavlos Vranas, André Walker-Loud, Towards grounding nuclear physics in QCD (arxiv:1910.07961)
the entirety of the rich field of nuclear physics emerges from QCD: from the forces binding protons and neutrons into the nuclear landscape, to the fusion and fission reactions between nuclei, to the prospective interactions of nuclei with BSM physics, and to the unknown state of matter at the cores of neutron stars.
How does this emergence take place exactly? How is the clustering of quarks into nucleons and alpha particles realized? What are the mechanisms behind collective phenomena in nuclei as strongly correlated many-body systems? How does the extreme fine-tuning required to reproduce nuclear binding energies proceed? – are big open questions in nuclear physics.
- Craig Roberts, Sebastian M. Schmidt, Reflections upon the Emergence of Hadronic Mass, The European Physical Journal Special Topics 229 (2020) 3319–3340 [doi:10.1140/epjst/e2020-000064-6, arXiv:2006.08782]
More than 98% of visible mass is contained within nuclei. In first approximation, their atomic weights are simply the sum of the masses of all the neutrons and protons (nucleons) they contain. Each nucleon has a mass GeV, i.e. approximately 2000-times the electron mass. The Higgs boson produces the latter, but what produces the masses of the neutron and proton? This is the question posed above, which is pivotal to the development of modern physics: how can science explain the emergence of hadronic mass (EHM)?
Modern science is thus encumbered with the fundamental problem of gluon and quark confinement; and confinement is crucial because it ensures absolute stability of the proton. Without confinement,our Universe cannot exist.
As the 21st Century began, the Clay Mathematics Institute established seven Millennium Prize Problems. Each represents one of the toughest challenges in mathematics. The set contains the problem of confinement; and presenting a sound solution will win its discoverer 1,000,000 bucks. Even with such motivation, today, almost fifty years after the discovery of quarks, no rigorous solution has been found. Confinement and EHM are inextricably linked. Consequently, as science plans for the next thirty years, solving the problem of EHM has become a grand challenge.
In trying to match QCD with Nature, one confronts the many complexities of strong, nonlinear dynamics in relativistic quantum field theory, e.g. the loss of particle number conservation, the frame and scale dependence of the explanations and interpretations of observable processes, and the evolving character of the relevant degrees-of-freedom. Electroweak theory and phenomena are essentially perturbative; hence, possess little of this complexity. Science has never before encountered an interaction such as that at work in QCD. Understanding this interaction, explaining everything of which it is capable, can potentially change the way we look at the Universe.
- Sourav Chatterjee: A probabilistic mechanism for quark confinement, Comm. Math. Phys. 385 (2021) 1007–1039 [doi:10.1007/s00220-021-04086-y, arXiv:2006.16229]
The confinement of quarks is one of the enduring mysteries ofmodern physics. [\ldots] In spite of many decades of research, physically relevant quantum gauge theories have not yet been constructed in a rigorous mathematical sense. non-perturbatively, that is] [] Perhaps the most important example is four-dimensional SU(3)-lattice gauge theory. If one can show that this theory has a mass gap at all values of the coupling strength, that would explain why particles known as glue-balls in the theory of strong interactions have mass. All such questions remain open.
The second big open question is the problem of quark confinement. Quarks are the constituents of various elementary particles, such as protons and neutrons. It is an enduring mystery why quarks are never observed freely in nature. The problem of quark confinement has received enormous attention in the physics literature, but the current consensus seems to be that a satisfactory theoretical explanation does not exist.
- Michael Creutz, QCD beyond diagrams (arXiv:2010.04774)
QCD, the theory of the strong interactions, involves quarks interacting with non-Abelian gluon fields. This theory has many features that are difficult to impossible to see in conventional diagrammatic perturbation theory. This includes quark confinement, mass generation, and chiral symmetry breaking.
- Craig Roberts, On Mass and Matter, AAPPS Bulletin 31 6 (2021) [doi:10.1007/s43673-021-00005-4, arXiv:2101.08340]
The origin of the proton mass, and with it the basic mass-scale for all nuclear physics, is one of the most profound puzzles in Nature.
Although QCD is defined by a seemingly simple Lagrangian, it specifies a problem that has defied solution for more than forty years. The key challenges in modern nuclear and high-energy physics are to reveal the observable content of strong QCD and, ultimately, therefrom derive the properties of nuclei.
- Guy de Teramond, Stanley Brodsky, Longitudinal dynamics and chiral symmetry breaking in holographic light-front QCD (arXiv:2103.10950)
In spite of the important progress of Euclidean lattice gauge theory, a basic understanding of the mechanism of color confinement and its relation to chiral symmetry breaking in QCD has remained an unsolved problem.
Recent developments based on superconformal quantum mechanics in light-front quantization and its holographic embedding on a higher dimensional gravity theory (gauge/gravity correspondence) have led to new analytic insights into the structure of hadrons and their dynamics.
- Igor Klebanov, Remarks on Color Confinement, talk at Strings 2021 (pdf, video)
Perhaps the gauge/string duality has provided us with a “physicist’s proof of confinement” in some exotic gauge theories like the one described by the warped deformed conifold. Yet, we still don’t have a quantitative handle on the Asymptotically Free theories in 3+1 dimensions. Don’t take confinement for granted, even in 1+1 dimensions where it seems obvious. Proof of Color Confinement in 2+1 and 3+1 dimensions would be very important.
-
Sergei Dubovsky, Comments on (mostly long) QCD strings, talk at Strings 2021 (pdf, pdf, video)
concludes in view of AdS/QCD:
With modern lattice tools and understanding of QFT/string theory we are in a good position to solve this problem. It may take another 30 years to build a new collider and get new data in particle physics. But we are lucky to have a tractable and fundamental problem to solve while waiting. Participants of STRINGS 2051 will be puzzled if we don’t make an effort now and leave it to them.
-
Clara Peset, Antonio Pineda, Oleksandr Tomalak, The proton radius (puzzle?) and its relatives (arXiv:2106.00695)
(in the context of the proton radius puzzle)
In the beginning God created quarks, And made them interact through the strong forces, And it was dark… And God said, “I do not understand a damn thing”
- Sophia K Domokos, Robert Bell, Trinh La, Patrick Mazza, A Pedagogical Introduction to Holographic Hadrons, published as: Holographic hadron masses in the language of quantum mechanics, European Journal of Physics 42 6 (2021) 065801 arXiv:2106.13136, doi:10.1088/1361-6404/ac1abb
We have known for over fifty years that protons are made up of quarks and gluons. We have pinned down the masses and couplings of quarks to a startling degree of accuracy. Yet we still don’t know why the proton’s mass is almost exactly a factor of 100 greater than the sum of the masses of its constituent quarks. This mystery persists because quarks and gluons are strongly coupled at low energies: they interact so forcefully and often that our usual calculational tools – based almost entirely on perturbation theory – fail.
Holographic duality, or “holographic QCD” (hQCD) when applied to hadrons, emerged in the early 2000s as a new way to tackle strongly coupled systems.
- Roman Pasechnik, Michal Šumbera, Different faces of confinement, Universe 7 (2021) 9, 330 (arXiv:2109.07600, doi:10.3390/universe7090330)
in the infrared (IR) limit, QCD enters entirely different, strongly-coupled domain, rendering the Perturbation Theory inapplicable and creating substantial problems for making reliable predictions at intermediate and low momentum transfers, i.e. at large distances. While it is conventionally believed that QCD should remain the correct theory of strong interactions also at large distances, in the so-called confined regime, deriving reliable predictions remains a big theoretical challenge.
The problem of confinement concerns the strongly-coupled sector of QCD composed of interacting colored partons (quarks and gluons). Despite the major efforts of the research community and tremendous progress made over last few decades, it does not appear to be fully and consistently resolved yet.
- Patrick Koppenburg for the LHCb collaboration: List of hadrons observed at the LHC (2021) pdf, webpage, cds:2749030
While the LHC is best known for the observation of the first fundamental scalar particle, the Higgs Boson, it has also yielded many observations of yet unknown hadrons. Hadrons are composed of quarks and are thus not fundamental particles of the Standard Model. However, their properties follow from yet unsolved mysteries of the strong interaction.
Although the QCD Lagrangian is expected to completely describe the spectrum of hadrons and all of their properties, there is no rigorous first-principle way of expressing this mathematically. The quark confinement conjecture is experimentally well tested, but mathematically still unproven. And it is still unknown which combinations of quarks may or may not form hadrons. Experimental guidance is needed to help improving theoretical models.
- Daniele Binosi, Emergent Hadron Mass in Strong Dynamics, Few-Body Syst 63 42 (2022) arXiv:2203.00942, doi:10.1007/s00601-022-01740-6
asymptotic freedom implies that the theory is innately nonperturbative at short distances, which in turn means that it is extremely difficult to describe QCD’s dynamics at the scale. Indeed, QCD’s colour-charged degrees of freedom, the massless gluons and the light up and down quarks, have never been observed in isolation: they are confined in colour-neutral bound-states, the hadrons, of which the (light) pion and the (heavy) proton are primary examples. It should be noticed that without a mass-scale confinement would not be possible: colour-singlet combinations of quarks would still be there, but the participating particles would need not be close together, since in a scale invariant theory all lengths are equivalent. Accordingly, the question “how does confinement appear in QCD” is inextricably connected to the question “how does mass emerge in strong dynamics”.
- Mikhail Shifman, OPE-based Methods in Nonperturbative QCD, Eur. Phys. J. C (2022) arXiv:2208.10600
QCD and its relatives are special because QCD is the theory of nature. QCD is strongly coupled in the infrared domain where it is impossible to treat it quasi-classically – perturbation theory fails even qualitatively. It does not capture drastic rearrangement of the vacuum structure related to confinement. The Lagrangian is defined at short distances in terms of gluons and quarks, while at large distances we deal with hadrons, e.g. pions, ρ mesons, protons, etc. Certainly, the latter are connected with quarks and gluons in a divine way, but this connection is highly nonlinear and non-local; even now, 50 years later, the full analytic solution of QCD is absent.
Non-perturbative methods were desperately needed.
-
Minghui Ding, Craig D. Roberts, Sebastian M. Schmidt, Emergence of Hadron Mass and Structure arXiv:2211.07763
-
Craig D. Roberts, Origin of the Proton Mass, at: 8th International Symposium on Symmetries in Subatomic Physics (SSP 2022) arXiv:2211.09905, doi:10.1051/epjconf/202328201006
(see the articles for a wealth of relevant commentary)
-
Guy de Téramond, Emergent phenomena in QCD: The holographic perspective arXiv:2212.14028
(discussion in holographic light front QCD)
At large distances, however, the nonperturbative nature of the strong interactions becomes dominant and a basic understanding of the essential features of hadron physics from first principles QCD has remained an important unsolved problem in the standard model of particle physics. Hadronic characteristics are not explicit properties of the QCD Lagrangian but emergent phenomena, notably, the origin of the hadron mass scale, the mechanism of color confinement, the relation between chiral symmetry breaking and confinement, the massless pion in the chiral limit (the limit of zero quark masses), bound states and the pattern of hadron excitations.
- Seth Grable, Paul Romatschke, Elements of Confinement for QCD with Twelve Massless Quarks arXiv:2310.12203]
Quantum Chromodynamics (QCD) is notorious for being a quantum field theory that is difficult to solve on large length scales what is missing in current QCD literature is a (potentially approximate) solution to continuum QCD that captures the main qualitative features such as confinement in the IR and asymptotic freedom in the UV if such a solution does exist, it cannot be based on a perturbative weak-coupling expansion, because QCD becomes strongly coupled towards long length scales. So the putative solution must arise from non-perturbative methods.
- The STAR Collaboration: Probing QCD Confinement with Spin Entanglement [arXiv:2506.05499]
The fundamental and literally million-dollar question is to understand the origin of these emergent hadron structures, e.g. mass and spin, which arise as a consequence of quark confinement. […] QCD [13], the theory of strong interactions, predicts that the strong force grows as the distance between partons increases, offering a qualitative explanation for confinement. However, as the distance scale approaches the typical length scale of a hadron, ∼ 1 fm ( meters), the complexity of first-principle QCD calculations becomes difficult to solve numerically at current computational power, due to the nature of low energy self-interacting gluons. This challenging regime, where simple approximations no longer work, is called nonperturbative QCD. Therefore, the detailed mechanisms through which confinement occurs from partons to hadrons, and how it manifests itself in hadron structure, remain unresolved puzzles [14].
Potential solutions
Via Skyrmions and D4-brane models
A good qualitative and moderate quantitative explanation of confinement in quantum chromodynamics is found in intersecting D-brane models, specifically in the Witten-Sakai-Sugimoto model which geometrically engineers QCD on D4-D8 brane bound states.
(Witten 98, followed up on in Sakai-Sugimoto 04, Sakai-Sugimoto 05)

graphics grabbed from Erlich 09, section 1.1
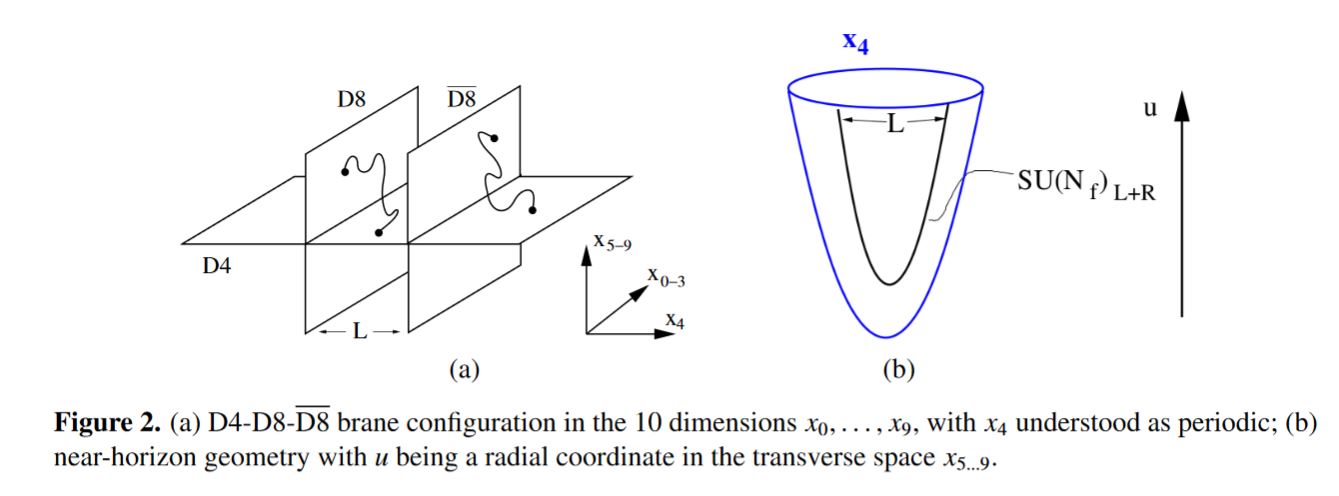
graphics grabbed from Rebhan 14
In this Witten-Sakai-Sugimoto model for strongly coupled QCD the hadrons in QCD correspond to string-theoretic-phenomena in the bulk field theory:
-
the mesons (bound states of 2 quarks) correspond to open strings in the bulk, whose two endpoints on the asymptotic boundary correspond to the two quarks
-
baryons (bound states of quarks) appear in two different but equivalent (Sugimoto 16, 15.4.1) guises:
-
as wrapped D4-branes with open strings connecting them to the D8-brane
-
as skyrmions
(Sakai-Sugimoto 04, section 5.2, Sakai-Sugimoto 05, section 3.3, see Bartolini 17).
-
For review see Sugimoto 16, also Rebhan 14, around (18).
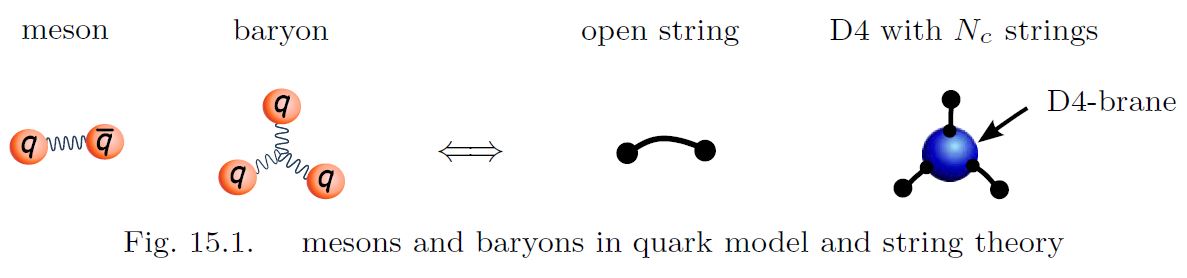
graphics grabbed from Sugimoto 16
Equivalently, these baryon states are the Yang-Mills instantons on the D8-brane giving the D4-D8 brane bound state (Sakai-Sugimoto 04, 5.7) as a special case of the general situation for Dp-D(p+4)-brane bound states (e.g. Tong 05, 1.4).
Strictly speaking, since the number of colors in quantum chromodynamics is not large (), an accurate formulation of such holographic QCD requires understanding small N corrections:
For more on this see at
and at
- skyrmion .
In super Yang-Mills theory via Seiberg-Witten theory
While confinement in plain Yang-Mills theory is still waiting for mathematical formalization and proof (see Jaffe-Witten), there is a variant of Yang-Mills theory with more symmetry, namely supersymmetry, where the phenomenon has been giving a decent argument, namely in N=2 D=4 super Yang-Mills theory (Seiberg-Witten 94).
Also a strategy for a proof for N=1 D=4 super Yang-Mills theory has been proposed, see below.
In super Yang-Mills theory via M-theory on -manifolds
An idea for a strategy towards a proof of confinement in N=1 D=4 super Yang-Mills theory via two different but conjecturally equivalent realizations as M-theory on G₂-manifolds has been given in Atiyah-Witten 01, section 6, review is in Acharya-Gukov 04, section 5.3.
The idea here is to consider a KK-compactification of M-theory on fibers which are G₂-manifolds that locally around a special point are of the form
where
-
is a finite subgroup of SU(2) that acts canonically by left-multiplication on SU(2);
-
denotes the metric cone construction.
This means that is a smooth manifold, but , as soon as is not the trivial group, , is an orbifold with an ADE singularity.
Now the lore of M-theory on G₂-manifolds predicts that KK-compactification
-
on yields a 4d theory without massless fields (since there are no massless modes on the covering space of )
-
on the ADE-singularity yields non-abelian Yang-Mills theory in 4d coupled to chiral fermions.
So in the first case a Yang-Mills mass gap is manifest, while non-abelian gauge theory is not visible, while in the second case it is the other way around.
But if there were an argument that M-theory on G₂-manifolds is in fact equivalent for compactification both on and on . To the extent that this is true, it looks like an argument that could demonstrate confinement in non-abelian 4d gauge theory.
This approach is suggested in Atiyah-Witten 01, pages 84-85. An argument that this equivalence is indeed the case is then provided in sections 6.1-6.4, based on an argument in Atiyah-Maldacena-Vafa 00
Via Calorons
It has been argued that, after Wick rotation, confinement may be derived from the behaviour of instantons (Schaefer-Shuryak 96, section III D), or rather their positive temperature-incarnations as calorons, Greensite 11, section 8.5:
it is natural to wonder if confinement could be derived from some semiclassical treatment of Yang–Mills theory based on the instanton solutions of non-abelian gauge theories. The standard instantons, introduced by Belavin et al. (40), do not seem to work; their field strengths fall off too rapidly to produce the desired magnetic disorder in the vacuum.
In recent years, however, it has been realized that instanton solutions at finite temperature, known as calorons, might do the job. These caloron solutions were introduced independently by Kraan and van Baal (41, 42) and Lee and Lu (43) (KvBLL), and they have the remarkable property of containing monopole constituents which may, depending on the type of caloron, be widely separated.
The caloron idea is probably the most promising current version of monopole confinement in pure non-abelian gauge theories, but it is basically (in certain gauges) a superposition of monopoles with spherically symmetric abelian fields, and this leads to the same questions raised in connection with monopole Coulomb gases.
See also at glueball.
Related concepts
effective field theories of nuclear physics, hence for confined-phase quantum chromodynamics:
References
In Yang-Mills theory
General
- Kenneth Wilson, Confinement of quarks, Phys. Rev. D 10 2445 (1974) [doi:10.1103/PhysRevD.10.2445]
Early demonstration of confinement by Monte Carlo simulation of lattice field theory (and demonstration that -gauge theory in 4d does not confine, as it should be):
- Michael Creutz, Confinement and the Critical Dimensionality of Space-Time, Phys. Rev. Lett. 43 (1979) 553 [doi:10.1103/PhysRevLett.43.553]
Textbook accounts:
-
Alexander Polyakov, Chapter V of: Gauge Fields and Strings, Routledge, Taylor and Francis (1987, 2021) [doi:10.1201/9780203755082, oapen:20.500.12657/50871]
-
David Griffiths, chapter 8 of: Introduction to Elementary Particles 2nd ed., Wiley-VCH (2008) [pdf, pdf, Wikipedia entry]
-
Jeff Greensite, An Introduction to the Confinement Problem, Lecture Notes in Physics, Volume 821, 2011 (doi:10.1007/978-3-642-14382-3)
-
Robert Iengo, section 9.1 of Quantum Field Theory (pdf)
-
D. Bugg (ed.), Hadron Spectroscopy and the Confinement Problem, Proceedings of a NATO Advanced Study Institute, Plenum Press 1996 (doi:10.1007/978-1-4613-0375-6)
-
Yakov Shnir, Section 9 of: Magnetic Monopoles, Springer 2005 (ISBN:978-3-540-29082-7)
(in view of Yang-Mills monopoles)
Introductions and surveys:
-
Yuri L. Dokshitzer, around section 1.2 of QCD Phenomenology (arXiv:hep-ph/0306287)
-
D. Espriu, section 7 of Perturbative QCD (arXiv:hep-ph/9410287)
-
Erhard Seiler, The Confinement Problem (pdf)
-
Roman Pasechnik, Michal Šumbera, Different faces of confinement, Universe 7 (2021) 9, 330 (arXiv:2109.07600, doi:10.3390/universe7090330)
See also:
-
Wikipedia, Color confinement
-
Prospects in Theoretical Physics 2023 – Understanding Confinement, IAS (2023)
-
The STAR Collaboration: Probing QCD Confinement with Spin Entanglement [arXiv:2506.05499]
-
Workshop on Non-perturbative Quantum Field Theory and Confinement, Carnegie Mellon University (May 28-31, 2025) [talks]
A formulation of confinement as an open problem of mathematical physics (see at Yang-Mills mass gap problem), together with many references:
- Arthur Jaffe, Edward Witten, Quantum Yang-Mills theory (pdf)
Other technical reviews:
-
G. M. Prosperi, Confinement and bound states in QCD (arXiv:hep-ph/0202186)
-
Christian Drischler, Wick Haxton, Kenneth McElvain, Emanuele Mereghetti, Amy Nicholson, Pavlos Vranas, André Walker-Loud, Towards grounding nuclear physics in QCD (arxiv:1910.07961)
-
Urko Reinosa, Aspects of confinement within non-Abelian gauge theories, lectures at QCD Masterclass, Saint-Jacut-de-la-Mer, June 2023 [arXiv:2404.06118]
See also:
-
Yuri A. Simonov, The fundamental scale of QCD (arXiv:2103.08223)
-
Duifje Maria van Egmond, Urko Reinosa, Julien Serreau, Matthieu Tissier, A novel background field approach to the confinement-deconfinement transition (arXiv:2104.08974)
-
Erich Poppitz, Notes on Confinement on : From Yang-Mills, super-Yang-Mills, and QCD(adj) to QCD(F) (arXiv:2111.10423)
Recognition of instantons and confinement in lattice gauge theory via topological data analysis (persistent homology):
- Daniel Spitz, Julian M. Urban, Jan M. Pawlowski, Confinement in non-Abelian lattice gauge theory via persistent homology [arXiv:2208.03955]
In relation to conformal symmetry and AdS-CFT duality (see also at AdS-QCD):
-
M. Kirchbach, T. Popov, J.-A. Vallejo, The Conformal-Symmetry – Color-Neutrality Connection in Strong Interaction [arXiv:2208.06484]
-
Canberk Güvendik, Thomas Schaefer, Mithat Ünsal, The metamorphosis of semi-classical mechanisms of confinement: From monopoles on to center-vortices on [arXiv:2405.13696]
-
E. G. Timoshenko, Boundary Effects and Confinement in the Theory of Nonabelian Gauge Fields, PhD thesis (1995) [arXiv:2405.13189]
See also:
-
M.S. Lukashov, Yu.A. Simonov, New ideas in nonperturbative QCD – I [arXiv:2406.05584]
-
J.L. Alonso, C. Bouthelier-Madre, J. Clemente-Gallardo, D. Martínez-Crespo: An axion-like mechanism for confinement in QCD [arXiv:2211.01047]
Via monopole condensation
An original suggestion that confinement in Yang-Mills theory may be understood via monopole condensation as a dual Meissner effect is due to
-
Gerard 't Hooft, in Proceed.of the Europ.Phys.Soc. 1975, ed.by A.Zichichi (Editrice Compositori, Bologna, 1976), p.1225.
-
S. Mandelstam, Phys.Rep. 23C (1976) 145;
(That this is indeed the case has not yet been demonstarted for plain Yang-Mills theory, but it was later shown for N=2 D=4 super Yang-Mills theory in (Seiberg-Witten 94). What this does or does not imply for the case of QCD is discussed in (Yung 00) ).
The relation to QCD instantons/monopoles in the QCD vacuum is discussed in
- T. Schaefer, Edward Shuryak, section III D of Instantons in QCD, Rev. Mod. Phys.70:323-426,1998 (arXiv:hep-ph/9610451)
and analogously (at positive temperature) relation to calorons:
-
P. Gerhold, E.-M. Ilgenfritz, M. Müller-Preussker, An KvBLL caloron gas model and confinement, Nucl.Phys.B760:1-37, 2007 (arXiv:hep-ph/0607315)
-
Rasmus Larsen, Edward Shuryak, Classical interactions of the instanton-dyons with antidyons, Nucl. Phys. A 950, 110 (2016) (arXiv:1408.6563)
-
Rasmus Larsen, Edward Shuryak, Interacting Ensemble of the Instanton-dyons and Deconfinement Phase Transition in the SU(2) Gauge Theory, Phys. Rev. D 92, 094022, 2015 (arXiv:1504.03341)
Further developments:
- Dimensional Transmutation by Monopole Condensation in QCD (arXiv:1206.6936)
Discussion of confinement via an interacting field vacuum
- Johann Rafelski, Vacuum structure – An Essay, in pages 1-29 of H. Fried, Berndt Müller (eds.) Vacuum Structure in Intense Fields, Plenum Press 1990 (GBooks)
See also:
- Yuri A. Simonov, Field Correlator Method for the confinement in QCD, Phys. Rev. D 99, 056012 (2019) (arXiv:1804.08946, doi:10.1103/PhysRevD.99.056012)
In super-insulators
An experimentally accessible analog of confinement is observed in superinsulators, where the role of quark-pairs is played by Cooper pairs:
-
M. Cristina Diamantini, Carlo A. Trugenberger, Valeri M. Vinokur: Confinement and Asymptotic Freedom with Cooper pairs, Nature Comm. Phys. 1 77 (2018) [arXiv:1807.01984, doi:10.1038/s42005-018-0073-9]
-
M. Cristina Diamantini, Carlo A. Trugenberger: Superinsulators: a toy realization of QCD in condensed matter, Ch. 23 in Roman Jackiw – 80th Birthday Festschrift, World Scientific (2020) 275-286 [arXiv:2008.12541]
Review:
-
Carlo A. Trugenberger: Superinsulators, Bose Metals and High- Superconductors: The Quantum Physics of Emergent Magnetic Monopoles, World Scientific (2022) [arXiv:10.1142/12688]
-
Carlo A. Trugenberger: Superinsulation: Magnetic Monopoles and Electric Confinement in Condensed Matter, talk at CQTS (Feb 2025) [slides:pdf]
-
Sebastian De Haro, Jeremy Butterfield, chaper 6 in:
The Philosophy and Physics of Duality, Cambridge University Press (2025) [arXiv:2508.01616, ISBN:9780198846338]
In super-Yang-Mills theory
Confinement in N=2 D=4 super Yang-Mills theory or super QCD by a version of the monopole condensation [‘t Hooft 75, Mandelstam 76] was demonstrated in
-
Nathan Seiberg, Edward Witten, Monopole Condensation, And Confinement In N=2 Supersymmetric Yang-Mills Theory, Nucl.Phys.B426:19-52,1994; Erratum-ibid.B430:485-486,1994 (arXiv:hep-th/9407087)
-
Nathan Seiberg, Edward Witten, Monopoles, Duality and Chiral Symmetry Breaking in N=2 Supersymmetric QCD, Nucl.Phys.B431:484-550,1994 (arXiv:hep-th/9408099)
Reviews with discussion of the impact on confinement in plain YM:
-
Alexei Yung, What Do We Learn about Confinement from the Seiberg-Witten Theory [arXiv:hep-th/0005088]
-
Michael Dine, On the Possibility of Demonstrating Confinement in Non-Supersymmetric Theories by Deforming Confining Supersymmetric Theories [arXiv:2211.17134]
-
Michael Dine: Larkin Award Colloquium, University of Santa Cruz, (Dec 2024) [video:YT]
See also:
- Michele Della Morte, Benjamin Jäger, Francesco Sannino, Justus Tobias Tsang, Felix P. G. Ziegler, The spectrum of QCD with one flavour: A Window for Supersymmetric Dynamics [arXiv:2302.10514]
Polyakov gauge/string duality
Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see notably also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical remarks in Polyakov (2008)) under the name gauge/string duality (cf. historical review in Polyakov (2008)), in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings:
Early suggestion that confined QCD is described by regarding the color-flux tubes as string-like dynamical degrees of freedoms:
-
John Kogut, Leonard Susskind, Vacuum polarization and the absence of free quarks in four dimensions, Phys. Rev. D 9 (1974) 3501-3512 [doi:10.1103/PhysRevD.9.3501]
-
Kenneth G. Wilson, Confinement of quarks, Phys. Rev. D 10 (1974) 2445 [doi:10.1103/PhysRevD.10.2445]
(argument in lattice gauge theory)
-
John Kogut, Leonard Susskind, Hamiltonian formulation of Wilson’s lattice gauge theories, Phys. Rev. D 11 (1975) 395 [doi:10.1103/PhysRevD.11.395]
“The gauge-invariant configuration space consists of a collection of strings with quarks at their ends. The strings are lines of non-Abelian electric flux. In the strong coupling limit the dynamics is best described in terms of these strings. Quark confinement is a result of the inability to break a string without producing a pair. […]”
“The confining mechanism is the appearance of one dimensional electric flux tubes which must link separated quarks. The appropriate description of the strongly coupled limit consists of a theory of interacting, propagating strings. […]”
“This picture of the strongly coupled Yang-Mills theory in terms of a collection of stringlike flux lines is the central result of our analysis. It should be compared with the phenomenological use of stringlike degrees of freedom which has been widely used in describing hadrons.”
-
Alexander Polyakov, String representations and hidden symmetries for gauge fields, Physics Letters B 82 2 (1979) 247-250 [doi:10.1016/0370-2693(79)90747-0]
-
Alexander Polyakov, Gauge fields as rings of glue, Nuclear Physics B 164 (1980) 171-188 [doi:10.1016/0550-3213(80)90507-6]
“The basic idea is that gauge fields can be considered as chiral fields, defined on the space of all possible contours (the loop space). The origin of the idea lies in the expectation that, in the confining phase of a gauge theory, closed strings should play the role of elementary excitations.”
-
Yuri Makeenko, Alexander A. Migdal, Quantum chromodynamics as dynamics of loops, Nuclear Physics B 188 2 (1981) 269-316 [doi:10.1016/0550-3213(81)90258-3]
“So the world sheet of string should be interpreted as the color magnetic dipole sheet. The string itself should be interpreted as the electric flux tube in the monopole plasma.”
-
Alexander Polyakov, Gauge Fields and Strings, Routledge, Taylor and Francis (1987, 2021) [doi:10.1201/9780203755082, oapen:20.500.12657/50871]
old personal page]: “My main interests this year [1993?] were directed towards string theory of quark confinement. The problem is to find the string Lagrangian for the Faraday’s ”lines of force“,which would reproduce perturbative corrections from the Yang-Mills theory to the Coulomb law at small distances and would give permanent confinement of quarks at large distances.”
Cf. also
-
M. Lüscher: Symmetry-breaking aspects of the roughening transition in gauge theories, Nuclear Physics B 180 2 (1981) 317-329 [doi:10.1016/0550-3213(81)90423-5]
-
Alexei Morozov, p. 6 of: String theory: what is it?, Sov. Phys. Usp. 35 (1992) 671-714 [doi:10.1070/PU1992v035n08ABEH002255]
Early suggestion, due to the Liouville field seen in the quantization of the bosonic string via the Polyakov action,
- Alexander Polyakov, Quantum geometry of bosonic strings, Phys. Lett. B 103 (1981) 207-210 [doi:10.1016/0370-2693(81)90743-7, pdf]
that such flux tubes regarded as confining strings are to be thought of a probing higher dimensional spacetime, exhibiting a holographic principle in which actual spacetime appears as a brane:
-
Alexander Polyakov, String Theory and Quark Confinement, talk at Strings’97, Nucl. Phys. Proc. Suppl. 68 (1998) 1-8 [doi:10.1016/S0920-5632(98)00135-2, arXiv:hep-th/9711002]
“In other words the open string flies in the -space keeping its feet (its ends) on the ground .”
-
Alexander Polyakov, The wall of the cave, Int. J. Mod. Phys. A 14 (1999) 645-658 arXiv:hep-th/9809057, doi:10.1142/S0217751X99000324
“We add new arguments that the Yang-Mills theories must be described by the non-critical strings in the five dimensional curved space. The physical meaning of the fifth dimension is that of the renormalization scale represented by the Liouville field.”
eventually culminating in the formulation of the dictionary for the AdS-CFT correspondence:
- Steven Gubser, Igor Klebanov, Alexander Polyakov, Gauge theory correlators from non-critical string theory, Physics Letters B 428 105-114 (1998) [doi:10.1016/S0370-2693(98)00377-3, hep-th/9802109]
“Relations between gauge fields and strings present an old, fascinating and unanswered question. The full answer to this question is of great importance for theoretical physics. It will provide us with a theory of quark confinement by explaining the dynamics of color-electric fluxes.”
- Alexander Polyakov, Vyacheslav Rychkov Gauge fields-strings duality and the loop equation, Nucl. Phys. B 581 (2000) 116-134 [doi:10.1016/S0550-3213(00)00183-8, arXiv:hep-th/0002106]
and the suggestion of finding the string-QCD correspondence:
- Alexander Polyakov, Gauge Fields and Space-Time, Int. J. Mod. Phys. A 17 S1 (2002) 119-136 [doi:10.1142/S0217751X02013071, arXiv:hep-th/0110196]
“in the strong coupling limit of a lattice gauge theory the elementary excitations are represented by closed strings formed by the color-electric fluxes. In the presence of quarks these strings open up and end on the quarks, thus guaranteeing quark confinement. Moreover, in the gauge theory the strings interaction is weak at large . This fact makes it reasonable to expect that also in the physically interesting continuous limit (not accessible by the strong coupling approximation) the best description of the theory should involve the flux lines (strings) and not fields, thus returning us from Maxwell to Faraday. In other words it is natural to expect an exact duality between gauge fields and strings. The challenge is to build a precise theory on the string side of this duality.”
Historical reminiscences:
- Alexander Polyakov, Confinement and Liberation, in Gerardus ’t Hooft (ed.) 50 Years of Yang-Mills Theory (2005) 311-329 [arXiv:hep-th/0407209, doi:10.1142/9789812567147_0013, doi:10.1142/5601]
“Already in 1974, in his famous large paper, ‘t Hooft already tried to find the string-gauge connections. His idea was that the lines of Feynman’s diagrams become dense in a certain sense and could be described as a 2d surface. This is, however, very different from the picture of strings as flux lines. Interestingly, even now people often don’t distinguish between these approaches. In fact, for the usual amplitudes Feynman’s diagrams don’t become dense and the flux lines picture is an appropriate one. However there are cases in which t’Hooft’s mechanism is really working.”
-
Alexander M. Polyakov, §1 in: Beyond Space-Time, in The Quantum Structure of Space and Time, Proceedings of the 23rd Solvay Conference on Physics, World Scientific (2007) [arXiv:hep-th/0602011, pdf]
-
Alexander M. Polyakov, From Quarks to Strings [arXiv:0812.0183]
published as Quarks, strings and beyond, section 44 in: Paolo Di Vecchia et al. (ed.), The Birth of String Theory, Cambridge University Press (2012) 544-551 [doi:10.1017/CBO9780511977725.048]
“By the end of ’77 it was clear to me that I needed a new strategy for understanding confinement and I became convinced that the way to go was the gauge/string duality. […]” “Classically the string is infinitely thin and has only transverse oscillations. But when I quantized it there was a surprise – an extra, longitudinal mode, which appears due to the quantum ”thickening“ of the string. This new field is called the Liouville mode. […]”
“I kept thinking about gauge/strings dualities. Soon after the Liouville mode was discovered it became clear to many people including myself that its natural interpretation is that random surfaces in 4d are described by the strings flying in 5d with the Liouville field playing the role of the fifth dimension. The precise meaning of this statement is that the wave function of the general string state depends on the four center of mass coordinates and also on the fifth, the Liouville one. In the case of minimal models this extra dimension is related to the matrix eigenvalues and the resulting space is flat.”
“Since this 5d space must contain the flat 4d subspace in which the gauge theory resides, the natural ansatz for the metric is just the Friedman universe with a certain warp factor. This factor must be determined from the conditions of conformal symmetry on the world sheet. Its dependence on the Liouville mode must be related to the renormalization group flow. As a result we arrive at a fascinating picture – our 4d world is a projection of a more fundamental 5d string theory. […]”
“At this point I was certain that I have found the right language for the gauge/string duality. I attended various conferences, telling people that it is possible to describe gauge theories by solving Einstein-like equations (coming from the conformal symmetry on the world sheet) in five dimensions. The impact of my talks was close to zero. That was not unusual and didn’t bother me much. What really caused me to delay the publication (Polyakov 1998) for a couple of years was my inability to derive the asymptotic freedom from my equations. At this point I should have noticed the paper of Klebanov 1997 in which he related D3 branes described by the supersymmetric Yang Mills theory to the same object described by supergravity. Unfortunately I wrongly thought that the paper is related to matrix theory and I was skeptical about this subject. As a result I have missed this paper which would provide me with a nice special case of my program. This special case was presented little later in full generality by Juan Maldacena (Maldacena 1997) and his work opened the flood gates.”
A detailed monograph:
-
N. D. Hari Dass, Strings to Strings – Yang-Mills Flux Tubes, QCD Strings and Effective String Theories, Lecture Notes in Physics 1018, Springer (2024) [doi:10.1007/978-3-031-35358-1]
Ch. 23:
Effective String Theories (EST) of Yang-Mills Flux Tubes [doi:10.1007/978-3-031-35358-1_22, arXiv:2312.10629]
Discussion of corrections of flux tube-dynamics beyond the Nambu-Goto action:
-
Michele Caselle, Nicodemo Magnoli, Alessandro Nada, Marco Panero, Dario Panfalone, Lorenzo Verzichelli: Confining strings in three-dimensional gauge theories beyond the Nambu–Gotō approximation, J. High Energ. Phys. 2024 198 (2024) [doi:10.1007/JHEP08(2024)198, arXiv:2407.10678]
-
Michele Caselle, Nicodemo Magnoli, Alessandro Nada, Marco Panero, Dario Panfalone, Lorenzo Verzichelli: Effective String Theory of three-dimensional gauge theories beyond the Nambu–Gotō approximation [arXiv:2412.14204]
Confinement via AdS/QCD correspondence
Polyakov’s ideas were eventually picked up by discussion of confinement in the AdS-QCD correspondence; see there for many references, including:
-
Edward Witten, Anti-de Sitter Space, Thermal Phase Transition, And Confinement In Gauge Theories, Adv. Theor. Math. Phys.2:505-532, 1998 (arXiv:hep-th/9803131)
-
David Berman, Maulik K. Parikh, Confinement and the AdS/CFT Correspondence, Phys.Lett. B483 (2000) 271-276 (arXiv:hep-th/0002031)
-
Henrique Boschi Filho, AdS/QCD and confinement, Seminar at t_Workshop on Strongly Coupled QCD: The confinement problem_ (November 2011) [pdf, pdf]
-
Edward Witten, Some Milestones in the Study of Confinement, talk at Prospects in Theoretical Physics 2023 – Understanding Confinement, IAS (2023) [web, YT]
40:13: “Personally, I think this setup really implies that pure gauge theory is dual to a string theory. The ‘only’ problem is that to get the pure gauge theory we need to make a relevant deformation and then take the limit that the deformation parameter is large…”
In M-theory on -manifolds
An idea for how to demonstrate confinement in models of M-theory on G₂-manifolds is given in
- Michael Atiyah, Edward Witten, section 6 of -Theory dynamics on a manifold of -holonomy, Adv. Theor. Math. Phys. 6 (2001) (arXiv:hep-th/0107177)
based on
- Michael Atiyah, Juan Maldacena, Cumrun Vafa, An M-theory Flop as a Large N Duality, J.Math.Phys.42:3209-3220, 2001 (arXiv:hep-th/0011256)
See also
- Bobby Acharya, Confining Strings from -holonomy spacetimes (arXiv:hep-th/0101206)
For review see
- Bobby Acharya, Sergei Gukov, section 5.3 of M theory and Singularities of Exceptional Holonomy Manifolds, Phys.Rept.392:121-189,2004 (arXiv:hep-th/0409191)
Last revised on August 5, 2025 at 06:22:08. See the history of this page for a list of all contributions to it.