nLab geometry of physics – basic notions of category theory
Basic notions of Category theory
We introduce here the basic notions of category theory, along with examples and motivation from geometry:
This constitutes what is sometimes called the language of categories. While we state and prove some basic facts here, notably the notorious Yoneda lemma (Prop. below), what makes category theory be a mathematical theory in the sense of a coherent collection of non-trivial theorems is all concerned with the topic of universal constructions, which may be formulated (only) in this language. This we turn to further below.
Categories and Functors
The notion of a category (Def. below) embodies the idea of structuralism applied to concepts in mathematics: it collects, on top of the set (or generally: class) of mathematical objects that belong to it, also all the structure-preserving maps between them, hence the homomorphisms in the case of Bourbaki-style mathematical structures.
The first achievement of the notion of a category is to abstract away from such manifestly concrete categories (Examples , below) to more indirectly defined mathematical objects whose “structure” is only defined, after the fact, by which maps, now just called morphisms, there are between them.
This structuralism-principle bootstraps itself to life by considering morphisms between categories themselves to be those “maps” that respect their structuralism, namely the connectivity and composition of the morphisms between their objects: These are the functors (Def. below).
For the purpose of geometry, a key class of examples of functors are the assignments of algebras of functions to spaces, this is Example below.
Definition
(category)
A category is
-
for each pair of objects, a set , called the set of morphisms from to , or the hom-set, for short.
We denote the elements of this set by arrows like this:
-
for each object a morphism
called the identity morphism on ;
-
for each triple of objects, a function
called composition;
such that:
-
for all pairs of objects unitality holds: given
then
-
for all quadruples of objects composition satifies associativity: given
then
The archetypical example of a category is the category of sets:
Example
The class of all sets with functions between them is a category (Def. ), to be denoted Set:
-
;
-
;
-
identity function on set ;
-
.
More generally all kind of sets with structure, in the sense going back to Bourbaki, form categories, where the morphisms are the homomorphisms (whence the name “morphism”!). These are called concrete categories (we characterize them precisely in Example , further below):
Example
(basic examples of concrete categories)
For a kind of mathematical structure, there is the category (Def. ) whose objects are the corresponding structured sets, and whose morphisms are the corresponding structure homomorphisms, hence the functions of underlying sets which respect the given structure.
Basic examples of concrete categories include the following:
This is the motivation for the terminology “categories”, as the examples in Example are literally categories of mathematical structures. But not all categories are “concrete” in this way.
Some terminology:
Definition
Let be a category (Def. ), then a directed graph with edges labeled by morphisms of the category is called a commuting diagram if for any two vertices any two ways of passing along edges from one to the other yields the same composition of the corresponding morphisms.
For example, a commuting triangle is
while a commuting square is
Definition
If a category (Def. ) happens to have as class of objects an actual set (i.e. a small set instead of a proper class), then is called a small category.
As usual, there are some trivial examples, that are however usefully made explicit for the development of the theory:
Example
(initial category and terminal category)
-
The terminal category is the category (Def. ) whose class of objects is the singleton set, and which has a single morphism on this object, necessarily the identity morphism.
-
The initial category or empty category is the category (Def. ) whose class of objects is the empty set, and which, hence, has no morphism whatsoever.
Clearly, these are small categories (Def. ).
Example
(preordered sets as thin categories)
Let be a preordered set. Then this induces a small category whose set of objects is , and which has precisely one morphism whenever , and no such morphism otherwise:
Conversely, every small category with at most one morphism from any object to any other, called a thin category, induces on its set of objects the structure of a partially ordered set via (1).
Here the axioms for preordered sets and for categories match as follows:
| reflexivity | transitivity | |
|---|---|---|
| partially ordered sets | ||
| thin categories | identity morphisms | composition |
Definition
For a category (Def. ), a morphism
is called an isomorphism if there exists an inverse morphism
namely a morphism such that the compositions with are equal to the identity morphisms on and , respectively
Definition
(groupoid)
If is a category in which every morphism is an isomorphism (Def. ), then is called a groupoid.
Example
For a group, there is a groupoid (Def. ) with a single object, whose single hom-set is , with identity morphism the neutral element and composition the group operation in :
In fact every groupoid with precisely one object is of the form.
Remark
(groupoids and homotopy theory)
Even though groupoids (Def. ) are special cases of categories (Def. ), the theory of groupoids in itself has a rather different flavour than that of category theory: Part of the homotopy hypothesis-theorem is that the theory of groupoids is really homotopy theory for the special case of homotopy 1-types.
(In applications in homotopy theory, groupoids are considered mostly in the case that the class of objects is in fact a set: small groupoids, Def. ).
For this reason we will not have more to say about groupoids here, and instead relegate their discussion to the section on homotopy theory, further below.
There is a range of constructions that provide new categories from given ones:
Example
(opposite category and formal duality)
Let be a category. Then its opposite category has the same objects as , but the direction of the morphisms is reversed. Accordingly, composition in the opposite category is that in , but with the order of the arguments reversed:
-
;
-
.
Hence for every statementa about some category there is a corresponding “dual” statement about its opposite category, which is “the same but with the direction of all morphisms reversed”. This relation is known as formal duality.
Example
Let and be two categories (Def. ). Then their product category has as objects pairs with and , and as morphisms pairs , , and composition is defined by composition in each entry:
-
;
Definition
(functor)
Let and be two categories (Def. ). A functor from to , to be denoted
is
such that
-
For each object the identity morphism is respected:
-
for each triple of objects, composition is respected: given
we have
Example
(categories of small categories and of small groupoids)
It is clear that functors (Def. ) have a composition operation given componentwise by the composition of their component functions. Accordingly, this composition is unital and associative. This means that there is
Example
Let be a category (Def. ). Then its hom-functor
is the functor (Def. ) out of the product category (Def. ) of with its opposite category to the category of sets, which sends a pair of objects to the hom-set between them, and which sends a pair of morphisms, with one of them into and the other out of , to the operation of composition with these morphisms:
Definition
(monomorphism and epimorphism)
Let be a category (Def. ). Then a morphism in is called
-
a monomorphism if for every object the hom-functor (Example ) out of takes to an injective function of hom-sets:
-
an epimorphism if for every object the hom-functor (Example ) into takes to an injective function:
Definition
(full, faithful and fully faithful functors)
A functor (Def. ) is called
-
a full functor if all its hom-functions are surjective functions
-
a faithful functor if all its hom-functions are injective functions
-
a fully faithful functor if all its hom-functions are bijective functions
A fully faithful functor is also called a full subcategory-inclusion. We will denote this situation by
Example
(full subcategory on a sub-class of objects)
Let be a category (Def. ) and let be a sub-class of its class of objects. The there is a category whose class of objects is , and whose morphisms are precisely the morphisms of , between these given objects:
with identity morphisms and composition defined as in . Then there is a fully faithful functor (Def. )
which is the evident inclsuion on objects, and the identity function on all hom-sets.
This is called the full subcategory of on the objects in .
Beware that not every fully faithful functor is, in components, exactly of this form, but, assuming the axiom of choice, every fully faithful functor is so up to equivalence of categories (Def. ).
The concept of faithful functor from Def. allows to make precise the idea of concrete category from Example :
Example
(structured sets and faithful functors)
Let be a kind of mathematical structure and let be the category of -structured sets. Then there is the forgetful functor
which sends each structured set to the underlying set (“forgetting” the structure that it carries), and which sends functions of sets to themselves. That a homomorphism of structured sets is a function between the underlying sets satisfying a special condition implies that this is a faithful functor (Def. ).
Conversely, it makes sense to define structured sets in general to be the objects of a category which is equipped with a faithful functor to the category of sets. See at structure for more on this.
Example
(spaces seen via their algebras of functions)
In any given context of geometry, there is typically a functor which sends any space of the given kind to its algebra of functions, and which sends a map (i.e. homomorphism) between the given spaces to the algebra homomorphism given by precomposition with that map (a hom-functor, Def. ). Schematically:
Since the precomposition operation reverses the direction of morphisms, as shown, these are functors from the given category of spaces to the opposite (Example ) of the relevant category of algebras.
In broad generality, there is a duality (“Isbell duality”) between geometry/spaces and algebra/algebras of functions) (“space and quantity”, Lawvere 86).
We now mention some concrete examples of this general pattern:
topological spaces and C*-algebras
Consider
-
the category Top of compact topological Hausdorff spaces with continuous functions between them;
-
the category C*Alg of unital C*-algebras over the complex numbers
Then there is a functor (Def. )
from the former to the opposite category of the latter (Example ) which sends any compact topological space to its C*-algebra of continuous functions with values in the complex numbers, and which sends every continuous function between compact spaces to the C*-algebra-homomorphism that is given by precomposition:
Part of the statement of Gelfand duality is that this is a fully faithful functor, hence exhibiting a full subcategory-inclusion (Def. ), namely that of commutative C*-algebras:
affine schemes and commutative algebras
The starting point of algebraic geometry is to consider affine schemes as the formal duals (Example ) of finitely generated commutative algebras over some algebraically closed ground field :
Beware that the immediate identification (2) is often obscured by the definition of affine schemes as locally ringed spaces. While the latter is much more complicated, at face value, in the end it yields an equivalent category (Def. below) to the simple formal dualization (Example ) in (2), see here. Already in 1973 Alexander Grothendieck had urged to abandon, as a foundational concept, the more complicated definition in favor of the simpler one in (2), see Lawvere 03.
smooth manifolds and real associative algebras
Consider
-
the category SmthMfd of smooth manifolds with smooth functions between them;
-
the category Alg of associative algebras over the real numbers
Then there is a functor (Def. )
from the former to the opposite category of the latter (Def. ), which sends any smooth manifold to its associative algebra of continuous functions to the real numbers, and which sends every smooth function between smooth manifolds to the algebra homomorphism that is given by precomposition:
The statement of Milnor's exercise is that this this is a fully faithful functor, hence exhibiting a full subcategory-inclusion (Def. ):
These two statements, expressing categories of spaces as full subcategories of opposite categories of categories of algebras, are the starting point for many developments in geometry, such as algebraic geometry, supergeometry, noncommutative geometry and noncommutative topology.
Since a fully faithful functor/full subcategory-embedding exhibits the objects of as a consistent generalization of the objects of , one may turn these examples around and define more general kinds of spaces as formal duals (Example ) to certain algebras:
infinitesimally thickened points and formal Cartesian spaces
The category of infinitesimally thickened points is, by definition, the full subcategory (Example ) of the opposite category (Example ) of that of commutative algebras (Example ) over the real numbers
on those with a unique maximal ideal which is a finite-dimensional as an -vector space and a nilradical: for each there exists such that .
The category of formal Cartesian spaces is, by definition, the full subcategory (Example ) of the opposite category (Example ) of that of commutative algebras (Example ) over the real numbers
on those which are tensor products of algebras, of an algebra of smooth functions on a Cartesian space , for some , and the algebra of functions on an infinitesimally thickened point.
Notice that the formal Cartesian spaces are fully defined by this assignment.
super points and super Cartesian spaces
The category of super points is by definition, the full subcategory (Example ) of the opposite category (Example ) of that of supercommutative algebras (Example ) over the real numbers
on the Grassmann algebras:
More generally, the category of super Cartesian spaces is by definition, the full subcategory
on the tensor product of algebras, over of the algebra of smooth functions on a Cartesian space, and a Grassmann algebra, as above.
Notice that the super Cartesian spaces are fully defined by this assignment. We discuss this in more detail in the chapter on supergeometry.
Natural transformations and presheaves
Given a system of (homo-)morphisms (“transformations”) in some category (Def. )
between objects that depend on some variable , hence that are values of functors of (Def. ), one says that this is natural, hence a natural transformation (Def. below) if it is compatible with (homo-)morphisms of the variable itself.
These natural transformations are the evident homomorphisms between functors
and hence there is a category of functors between any two categories (Example below).
A key class of such functor categories are those between an opposite category and the base category of sets, these are also called categories of presheaves (Example below). It makes good sense (Remark below) to think of these as categories of “generalized objects of ”, a perspective which is made precise by the statement of the Yoneda lemma (Prop. below) and the resulting Yoneda embedding (Prop. below). This innocent-looking lemma is the heart that makes category theory tick.
Definition
(natural transformation and natural isomorphism)
Given two categories and (Def. ) and given two functors and from to (Def. ), then a natural transformation from to
is
such that
-
for each morphism we have a commuting square (Def. ) of the form
(4)(sometimes called the naturality square of the natural transformation).
If all the component morphisms are isomorphisms (Def. ), then the natural transformation is called a natural isomorphism.
For
two natural transformations as shown, their composition is the natural transformation
whose components (3) are the compositions of the components of and :
Example
(reduction of formal Cartesian spaces)
On the category FormalCartSp of formal Cartesian spaces Example , consider the endofunctor
which sends each formal Cartesian space to the underlying ordinary Cartesian space, forgetting the infinitesimally thickened point-factor. Moreover, on morphisms this functor is defined via the retraction
as
This is indeed functorial due to the fact that any algebra homomorphism needs to send nilpotent elements to nilpotent elements, so that the following identity holds:
Then there is a natural transformation (Def. ) from this functor to the identity functor
whose components inject the underlying Cartesian space along the unit point inclusion of the infinitesimally thickened point:
The commutativity of this naturality square is again the identity (6).
Example
Let and be categories (Def. ). Then the category of functors between them, to be denoted , is the category whose objects are the functors (Def. ) and whose morphisms are the natural transformations between functors (Def. ) and whose composition operation is the composition of natural transformations (5).
Example
Given a category (Def. ), a functor (Def. ) of the form
hence out of the opposite category of (Def. ), into the category of sets (Example ) is also called a presheaf (for reasons discussed below) on or over .
The corresponding functor category (Example )
is hence called the category of presheaves over .
Example
Given a category (Def. ), the hom-functor (Example ) induces the following functor (Def. ) from to its category of presheaves (Def. ):
The presheaves in the image of this functor are called the representable presheaves and is called their representing object.
The functor (7) is also called the Yoneda embedding, due to Prop. below.
Remark
(presheaves as generalized spaces)
If a given category (Def. ) is thought of as a category of spaces of sorts, as those in Example , then it will be most useful to think of the corresponding category of presheaves (Def. ) as a category of generalized spaces probe-able by the test spaces in (Lawvere 86, p. 17).
Namely, imagine a generalized space which is at least probe-able by spaces in . This should mean that for each object there is some set of geometric maps “”. Here the quotation marks are to warn us that, at this point, is not defined yet; and even if it were, it is not expected to be an object of , so that, at this point, an actual morphism from to is not definable. But we may anyway consider some abstract set
whose elements we do want to think of maps (homomorphisms of spaces) from to .
That this is indeed consistent, in that we may actually remove the quotation remarks on the right of (8), is the statement of the Yoneda lemma, which we discuss as Prop. below.
A minimum consistency condition for this to make sense (we will consider further conditions later on when we discuss sheaves) is that we may consistently pre-compose the would-be maps from to with actual morphisms in . This means that for every such morphism there should be a function between these sets of would-be maps
which respects composition and identity morphisms. But in summary, this says that what we have defined thereby is actually a presheaf on (Def. ), namely a functor
For consistency of regarding this presheaf as a presheaf of sets of plots of a generalized space, it ought to be true that every “ordinary space”, hence every object , is also an example of a “generalized space probe-able by” object of , since, after all, these are the spaces which may manifestly be probed by objects , in that morphisms are already defined.
Hence the incarnation of as a generalized space probe-able by objects of should be the presheaf , hence the presheaf represented by (Example ), via the Yoneda functor (7).
At this point, however, a serious consistency condition arises: The “ordinary spaces” now exist as objects of two different categories: on the one hand there is the original , on the other hand there is its Yoneda image in the category of generalized spaces. Hence we need to know that these two perspectives are compatible, notably that maps between ordinary spaces are the same whether viewed in or in the more general context of .
That this, too, holds true, is the statement of the Yoneda embedding, which we discuss as Prop. below.
Eventually one will want to impose one more consistency condition, namely that plots are determined by their local behaviour. This is the sheaf condition (Def. below) and is what leads over from category theory to topos theory below.
Proposition
Let be a category (Def. ), any object, and a presheaf over (Def. ).
Then there is a bijection
between the hom-set of the category of presheaves from the presheaf represented by (7) to , and the set which is assigned by to .
Proof
By Example , an element in the set on the left is a natural transformation (Def. ) of the form
hence given by component functions (3)
for each . In particular there is the component at
and the identity morphism on is a canonical element in the set on the left. The statement to be proven is hence equivalently that for every element in there is precisely one such that this element equals .
Now the condition to be satisfied by is that it makes its naturality squares (4) commute (Def. ). This includes those of the form
for any morphism
As the diagram chase of elements on the right shows, this commutativity (Def. ) fixes for all and all uniquely in terms of the element .
It remains only to see that there is no condition on the element , hence that with defined this way, the commutativity of all the remaining naturality squares is implies: The general naturality square for a morphism is of the form
As shown on the right, the commutativity of this diagram now follows from the functoriality of the presheaf .
As a direct corollary, we obtain the statement of the Yoneda embedding:
Proposition
The assignment (7) of represented presheaves (Example ) is a fully faithful functor (Def. ), hence exhibits a full subcategory inclusion
of the given category into its category of presheaves.
Proof
We need to show that for all the function
is a bijection. But the Yoneda lemma (Prop. ) states a bijection the other way around
and hence it is sufficient to see that this is a left inverse to (9). This follows by inspection, as shown in the third line above.
As a direct corollary we obtain the following alternative characterization of isomorphisms, to be compared with the definition of epimorphisms/monomorphisms in Def. :
Example
(isomorphism via bijection of hom-sets)
Let be a category (Def. ), let be a pair of objects, and let be a morphism between them. Then the following are equivalent:
-
is an isomorphism (Def. ),
-
the hom-functors into and out of take values in bijections of hom-sets: i.e. for all objects , we have
and
Adjunctions
The concepts of categories, functors and natural transformations constitute the “language of categories”. This language now allows to formulate the concept of adjoint functors (Def. ) and more generally that of adjunctions (Def. below. This is concept that category theory, as a theory, is all about.
Part of the data involved in an adjunction is its adjunction unit and adjunction counit (Def. below) and depending on their behaviour special cases of adjunctions are identified (Prop. below), which we discuss in detail in following sections:
| adjunction Def. , Def. | unit is iso: | |
| coreflection Def. | ||
| counit is iso: | reflection Def. | adjoint equivalence Def. |
We now discuss four equivalent definitions of adjoint functors:
-
via adjunction unit and -counit satisfying triangle identities (Prop. );
-
via representing objects (Prop. );
-
via universal morphisms (Prop. below).
Then we discuss some key properties:
Definition
Let and be two categories (Def. ), and let
be a pair of functors between them (Def. ), as shown. Then this is called a pair of adjoint functors (or an adjoint pair of functors) with left adjoint and right adjoint, denoted
if there exists a natural isomorphism (Def. ) between the hom-functors (Example ) of the following form:
This means that for all objects and there is a bijection of hom-sets
which is natural in and . This isomorphism is called the adjunction hom-isomorphism and the image of a morphism under this bijections is called the adjunct of . Conversely, is called the adjunct of .
Naturality here means that for every pair of morphisms in and in , the resulting square
commutes (Def. ), where the vertical morphisms are given by the hom-functor (Example ).
Explicitly, this commutativity, in turn, means that for every morphism with adjunct , the adjunct of the composition is
Definition
(adjunction unit and counit)
Given a pair of adjoint functors
according to Def. , one says that
-
for any the adjunct of the identity morphism on is the unit morphism of the adjunction at that object, denoted
-
for any the adjunct of the identity morphism on is the counit morphism of the adjunction at that object, denoted
Remark
It happens that there are sequences of adjoint functors:
If two functors are adjoint to each other as in Def. , we also say that we have an adjoint pair:
It may happen that one functor participates on the right and on the left of two such adjoint pairs and (not the same “” and “” as before!) in which case one may speak of an adjoint triple:
Below in Example we identify adjoint triples as adjunctions of adjunctions.
Similarly there are adjoint quadruples, etc.
Notice that in the case of an adjoint triple (12), the adjunction unit of and the adjunction counit of (Def. ) provide, for each object in the domain of , a diagram
which is usefully thought of as exhibiting the nature of as being in between two opposite extreme aspects and of . This is illustrated by the following examples, and formalized by the concept of modalities that we turn to in Def. below.
Example
(floor and ceiling as adjoint functors)
Consider the canonical inclusion
of the integers into the real numbers, both regarded as preorders in the standard way (“lower or equal”). Regarded as full subcategory-inclusion (Def. ) of the corresponding thin categories, via Example , this inclusion functor has both a left and right adjoint functor (Def. ):
-
the left adjoint to is the ceiling function;
-
the right adjoint to is the floor function;
forming an adjoint triple (Def. )
The adjunction unit and adjunction counit express that each real number is in between its “opposite extreme integer aspects” (13) given by floor and ceiling
Proof
First of all, observe that we indeed have functors (Def. )
since floor and ceiling preserve the ordering relation.
Now in view of the identification of preorders with thin categories in Example , the hom-isomorphism (10) defining adjoint functors of the form says for all and , that we have
This is clearly already the defining condition on the floor function .
Similarly, the hom-isomorphism defining adjoint functors of the form says that for all and , we have
This is evidently already the defining condition on the floor function .
Notice that in both cases the condition of a natural isomorphism in both variables, as required for an adjunction, is automatically satisfied: For let and , then naturality as in (11) means, again in view of the identifications in Example , that
Here the logical implications are equivalently functions between sets that are either empty or singletons. But Functions between such sets are unique, when they exist.
Example
(discrete and codiscrete topological spaces)
Consider the “forgetful functor” from the category Top of topological spaces (Example ) to the category of sets (Def. ) which sends every topological space to its underlying set.
This has
-
a left adjoint (Def. ) which equips a set with its discrete topology,
-
a right adjoint which equips a set with the codiscrete topology.
These hence form an adjoint triple (Remark )
Hence the adjunction counit of and the adjunction unit of exhibit every topology on a given set as “in between the opposite extremes” (13) of the discrete and the co-discrete
Lemma
(pre/post-composition with (co-)unit followed by adjunct is adjoint functor)
If a functor is the right adjoint
in a pair of adjoint functors (Def. ), then its application to any morphism is equal to the joint operation of pre-composition with the -adjunction counit (Def. ), followed by passing to the -adjunct:
Dually, if is a left adjoint
then its action on any morphism equals the joint operation of post-composition with the -adjunction unit (Def. ), followed by passing to the -adjunct:
In particular, if is the middle functor in an adjoint triple (Remark )
then these two operations coincide:
Proof
For the first equality, consider the following naturality square (4) for the adjunction hom-isomorphism (10):
Chasing the identity morphism through this diagram yields the claimed equality, as shown on the right. Here we use that the left adjunct? of the identity morphism is the adjunction counit, as shown.
The second equality is fomally dual:
We now turn to a sequence of equivalent reformulations of the condition of adjointness.
Proposition
(general adjuncts in terms of unit/counit)
Consider a pair of adjoint functors
according to Def. , with adjunction units and adjunction counits according to Def. .
Then
-
The adjunct of any morphism is obtained from and as the composite
(16)Conversely, the adjunct of any morphism is obtained from and as
(17) -
The adjunction units and adjunction counits are components of natural transformations of the form
and
-
The adjunction unit and adjunction counit satisfy the triangle identities, saying that
(18)and
Proof
For the first statement, consider the naturality square (11) in the form
and consider the element in the top left entry. Its image under going down and then right in the diagram is , by Def. . On the other hand, its image under going right and then down is , by Def. . Commutativity of the diagram means that these two morphisms agree, which is the statement to be shown, for the adjunct of .
The converse formula follows analogously.
The third statement follows directly from this by applying these formulas for the adjuncts twice and using that the result must be the original morphism:
For the second statement, we have to show that for every moprhism the following square commutes:
To see this, consider the naturality square (11) in the form
The image of the element in the top left along the right and down is , by Def. , while its image down and then to the right is , by the previous statement. Commutativity of the diagram means that these two morphisms agree, which is the statement to be shown.
The argument for the naturality of is directly analogous.
Proposition
(adjoint functors equivalent to adjunction in Cat)
Two functors
are an adjoint pair in the sense that there is a natural isomorphism (10) according to Def. , precisely if they participate in an adjunction in the 2-category Cat, meaning that
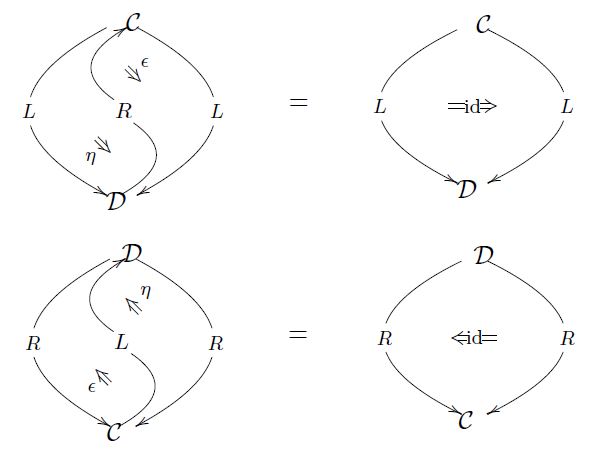
-
there exist natural transformations
and
-
which satisfy the triangle identities
and
Proof
That a hom-isomorphism (10) implies units/counits satisfying the triangle identities is the statement of the second two items of Prop. .
Hence it remains to show the converse. But the argument is along the same lines as the proof of Prop. : We now define forming of adjuncts by the formula (16). That the resulting assignment is an isomorphism follows from the computation
where, after expanding out the definition, we used naturality of and then the triangle identity.
Finally, that this construction satisfies the naturality condition (11) follows from the functoriality of the functors involved, and the naturality of the unit/counit:
The condition (10) on adjoint functors in Def. implies in particular that for every object the functor is a representable functor with representing object . The following Prop. observes that the existence of such representing objects for all is, in fact, already sufficient to imply that there is a right adjoint functor.
This equivalent perspective on adjoint functors makes manifest that adjoint functors are, if they exist, unique up to natural isomorphism, this is Prop. below.
Proposition
(adjoint functor from objectwise representing objects)
A functor has a right adjoint , according to Def. , already if for all objects there is an object such that there is a natural isomorphism
hence for each object a bijection
such that for each morphism , the following diagram commutes
(This is as in (11), except that only naturality in the first variable is required.)
In this case there is a unique way to extend from a function on objects to a function on morphisms such as to make it a functor which is right adjoint to . , and hence the statement is that with this, naturality in the second variable is already implied.
Proof
Notice that
-
in the language of presheaves (Example ) the assumption is that for each the presheaf
is represented (7) by the object , and naturally so.
-
In terms of the Yoneda embedding (Prop. )
we have
(20)
The condition (11) says equivalently that has to be such that for all morphisms the following diagram in the category of presheaves commutes
This manifestly has a unique solution
for every morphism under (20). But the Yoneda embedding is a fully faithful functor (Prop. ), which means that thereby also is uniquely fixed.
We consider one more equivalent characterization of adjunctions:
Definition
Let be two categories (Def. ) and let be a functor (Def. )
Then for an object, a universal morphism from to is
such that for any , any morphism factors through this unit as
for a unique morphism , to be called the adjunct of .
Proposition
(collection of universal morphisms equivalent to adjoint functor)
Let be a functor (Def. ). Then the following are equivalent:
-
has a left adjoint functor according to Def. .
-
For every object there is a universal morphism , according to Def. .
Proof
In one direction, assume a left adjoint is given. Define the would-be universal arrow at to be the unit of the adjunction via Def. . Then the statement that this really is a universal arrow is implied by Prop. .
In the other direction, assume that universal arrows are given. The uniqueness clause in Def. immediately implies bijections
Hence to satisfy (10) it remains to show that these are natural in both variables. In fact, by Prop. it is sufficient to show naturality in the variable . But this is immediate from the functoriality of applied in (21): For any morphism, we have
The following equivalent formulation (Prop. ) of universal morphisms is often useful:
Example
Let be a category, let be any object, and let be a functor.
-
The comma category is the category whose objects are pairs consisting of an object and morphisms in , and whose morphisms are the morphisms in that make a commuting triangle (Def. ):
There is a canonical functor
-
The comma category is the category whose objects are pairs consisting of an object and a morphism in , and whose morphisms are the morphisms in that make a commuting triangle (Def. ):
Again, there is a canonical functor
(22)
With this definition, the following is evident:
Proposition
(universal morphisms are initial objects in the comma category)
Let be a functor and an object. Then the following are equivalent:
-
is a universal morphism into (Def. );
-
is the initial object (Def. ) in the comma category (Example ).
After these equivalent characterizations of adjoint functors, we now consider some of their main properties:
Proposition
(adjoint functors are unique up to natural isomorphism)
The left adjoint or right adjoint to a functor (Def. ), if it exists, is unique up to natural isomorphism (Def. ).
Proof
Suppose the functor is given, and we are asking for uniqueness of its right adjoint, if it exists. The other case is directly analogous.
Suppose that are two functors which both are right adjoint to . Then for each the corresponding two hom-isomorphisms (10) combine to say that there is a natural isomorphism/
As in the proof of Prop. , the Yoneda lemma implies that
for some isomorphism
But then the uniqueness statement of Prop. implies that the collection of these isomorphisms for each object constitues a natural isomorphism between the functors (Def. ).
Proposition
(characterization of epi/mono/iso (co-)unit of adjunction)
Let
be a pair of adjoint functors (Def. ).
Recall the definition of
-
adjunction unit/counit, from Def. )
-
faithful/fully faithful functor from Def.
-
mono/epi/isomorphism from Def. and Def. .
The following holds:
-
is faithful precisely if all components of the counit are epimorphisms ;
-
is faithful precisely if all components of the unit are monomorphisms
-
is full and faithful (exhibits a reflective subcategory, Def. ) precisely if all components of the counit are isomorphisms
-
is full and faithful (exhibits a coreflective subcategory, def. ) precisely if all component of the unit are isomorphisms .
Proof
This follows directly by Lemma , using the definition of epi/monomorphism (Def. ) and the characterization of isomorphism from Example .
To complete this pattern, we will see below in Prop. that following are equivalent:
-
the unit and counit are both natural isomorphism, hence and are both fully faithful;
-
is an equivalence (Def. );
-
is an equivalence (Def. )
-
is an adjoint equivalence (Def. ).
Proposition
(right/left adjoint functors preserve monomorphism/epimorphisms and terminal/initial objects)
Every right adjoint functor (Def. ) preserves
-
terminal objects (Def. ),
-
monomorphisms (Def. )
Every left adjoint functor (Def. ) preserves
-
initial objects (Def. ),
-
epimorphisms (Def. ).
Proof
This is immediate from the adjunction hom-isomorphism (10), but we spell it out:
We consider the first case, the second is formally dual (Example ). So let be a right adjoint functor with left adjoint .
Let be a terminal object (Def. ). We need to show that for every object the hom-set is a singleton. But by the hom-isomorphism (10) we have a bijection
where in the last step we used that is a terminal object, by assumption.
Next let be a monomorphism. We need to show that for any object, the hom-functor out of yields a monomorphism
Now consider the following naturality square (11) of the adjunction hom-isomorphism (10):
Here the right vertical function is an injective function, by assumption on and the definition of monomorphism. Since the two horizontal functions are bijections, this implies that also is an injection.
But the main preservation property of adjoint functors is that adjoints preserve (co-)limits. This we discuss as Prop. below, after introducing limits and colimits in Def. below.
Prop. says that adjoint functors are equivalenty “adjunctions in Cat”, as defined there. This is a special case of a general more abstract concept of adjunction, that is useful:
Definition
A strict category is
-
for each pair of objects, a small category (Def. ), called the hom-category from to .
We denote the objects of this hom-category by arrows like this:
and call them the 1-morphisms of ,
and we denote the morphisms in the hom-category by double arrows, like this:
and call these the 2-morphisms of ;
-
for each object a 1-morphism
called the identity morphism on ;
-
for each triple of objects, a functor (Def. )
from the product category (Example ) of hom-categories, called composition;
such that:
-
for all pairs of objects unitality holds:
the functors of composition with identity morphisms are identity functors
-
for all quadruples of objects composition satifies associativity, in that the following two composite functors are equal:
The archetypical example of a strict 2-category is the category of categories:
Example
There is a strict 2-category (Def. ) Cat whose
-
objects are small categories (Def. );
-
1-morphisms are functors (Def. );
-
2-morphisms are natural transformations (Def. )
with the evident composition operations.
With a concept of 2-category in hand, we may phrase Prop. more abstractly:
Definition
(adjunction in a 2-category)
Let be a strict 2-category (Def. ). Then an adjunction in is
-
called the left adjoint and right adjoint ;
-
, called the adjunction unit
, called the adjunction counit
such that the following triangle identities hold:

We denote this situation by
Hence via Example , Prop. says that an adjoint pair of functors is equivalente an adjunction in the general sense of Def. , realized in the very large strict 2-category Cat of categories.
This more abstract perspecive on adjunctions allow us now to understand “duality of dualities” as adjunction in a 2-category of adjunctions:
Example
(strict 2-category of categories with adjoint functors between them)
Let be the strict 2-category which is defined just as Cat (Def. ) but with the 1-morphisms being functors that are required to be left adjoints (Def. ).
Since adjoints are unique up to natural isomorphism (Prop. ), this may be thought of as a 2-category whose 1-morphisms are adjoint pairs of functors.
Example
(adjunctions of adjoint pairs are adjoint triples)
An adjunction (Def. ) in the 2-category of categories with adjoint functors between them (Example ) is equivalently an adjoint triple of functors (Remark ):
The adjunction says that two left adjoint functors and , which, hence each participate in an adjoint pair
form themselves an adjoint pair
By essentiall uniqueness of adjoints (Prop. ) this implies a natural isomorphism and hence an adjoint triple:
Example suggest to consider a slight variant of the concept of strict 2-categories which allows to make the duality between left adjoints and right adjoints explicit:
Definition
A double category is
-
a pair of categories , (Def. ) which share the same class of objects: , to be called the class of objects of
where the morphisms of are to be called the horizontal morphisms of ,
while the morphisms of are to be called the vertical morphisms of ,
-
for each quadruple of objects and pairs of pairs of horizontal/vertical morphisms of the form
a set , to be called the set of 2-morphisms of between the given 1-morphisms, whose elements we denote by
-
a horizontal and a vertical composition operation of 2-morphisms which is unitality and associative in both directions in the evident way, which respects composition in and , and such that horizontal and vertical composition commute over each other in the evident way.
Example
(double category of squares of a strict 2-category)
Let be a strict 2-category (Def. ). Then its double category of squares is the double category (Def. ) whose
-
objects are those of ;
-
horizontal morphisms and vertical morphisms are both the 1-morphisms of ;
-
are the 2-morphisms of between the evident composites of 1-morphisms:
and composition is given by the evident compositions in .
Remark
(strict and weak 2-functors)
Given two strict 2-categories (Def. ) or double categories (Def. ), , there is an evident notion of 2-functor or double functor
between them, namely functions on objects, 1-morphisms and 2-morphisms which respect all the composition operations and identity morphisms.
These are also called strict 2-functors.
This is in contrast to a more flexible concept of weak 2-functors, often called pseudofunctors, which respect composition of 1-morphisms only up to invertible 2-morphisms (which themselves are required to satisfy some coherence condition):
We will see an important example of a weak double functor in the construction of derived functors of Quillen functors, below in Prop. .
Equivalences
We have seen functors (Def. ) as the homomorphisms between categories (Def. ). But functors themselves are identified only up to natural isomorphism (Def. ), reflective the fact that they are the 1-morphisms in a 2-category of categories (Example ). This means that in identifying two categories, we should not just ask for isomorphisms between them, hence for a functor between them that has a strict inverse morphism, but just for an inverse up to natural isomorphism.
This is called an equivalence of categories (Def. below). A particularly well-behaved equivalence of categories is an equivalence exhibited by an adjoint pair of functors, called an adjoint equivalence of categories (Def. below). In fact every equivalence of categories may be improved to an adjoint equivalence (Prop. ).
Definition
(adjoint equivalence of categories)
Let , be two categories (Def. ). Then an adjoint equivalence of categories between them is a pair adjoint functors (Def. )
such that their unit and counit (Def. ) are natural isomorphisms (as opposed to just being natural transformations)
There is also the following, seemingly weaker, notion:
Definition
Let , be two categories (Def. ). Then an equivalence of categories
is a pair of functors back and forth, as shown (Def. ), together with natural isomorphisms (Def. ) between their composition and the identity functors:
If a functor participates in an equivalence of categories, that functor alone is usually already called an equivalence of categories. If there is any equivalence of categories between two categories, these categories are called equivalent.
Proposition
(every equivalence of categories comes from an adjoint equivalence of categories)
Let and be two categories (Def. ). Then the they are equivalent (Def. ) precisely if there exists an adjoint equivalence of categories between them (Def. ).
Moreover, let be a functor (Def. ) which participates in an equivalence of categories (Def. ). Then for every functor equipped with a natural isomorphism
there exists a natural isomorphism
which completes this to an adjoint equivalence of categories (Def. ).
Inside every adjunction sits its maximal adjoint equivalence:
Proposition
(fixed point equivalence of an adjunction)
Let
be a pair of adjoint functors (Def. ). Say that
-
an object is a fixed point of the adjunction if its adjunction unit (Def. ) is an isomorphism (Def. )
and write
for the full subcategory on these fixed objects (Example )
-
an object is a fixed point of the adjunction if its adjunction counit (Def. ) is an isomorphism (Def. )
and write
for the full subcategory on these fixed objects (Example )
Then the adjunction (co-)restrics to an adjoint equivalence (Def. ) on these full subcategories of fixed points
Proof
It is sufficient to see that the functors (co-)restrict as claimed, for then the restricted adjunction unit/counit are isomorphisms by definition, and hence exhibit an adjoint equivalence.
Hence we need to show that
-
for we have that is an isomorphism;
-
for we have that is an isomorphism.
For the first case we claim that provides an inverse: by the triangle identity (18) it is a right inverse, but by assumption it is itself an invertible morphism, which implies that is an isomorphism.
The second claim is formally dual.
Modalities
Generally, a full subcategory-inclusion (Def. ) may be thought of as a consistent proposition about objects in a category: The objects in the full subcategory are those that have the given property.
This basic situation becomes particularly interesting when the inclusion functor has a left adjoint or a right adjoint (Def. ), in which case one speaks of a reflective subcategory, or a coreflective subcategory, respectively (Def. below). The adjunction now implies that each object is reflected or coreflected into the subcategory, and equipped with a comparison morphism to or from its (co-)reflection (the adjunction (co-)unit, Def. ). This comparison morphism turns out to always be an idempotent (co-)projection, in a sense made precise by Prop. below.
This means that, while any object may not fully enjoy the property that defines the subcategory, one may ask for the “aspect” of it that does, which is what is (co-)projected out. Regarding objects only via these aspects of them hence means to regard them only locally (where they exhibit that aspect) or only in the mode of focus on this aspect. Therefore one also calls the (co-)reflection operation into the given subcategory a (co-)localization or (co-)modal operator, or modality, for short (Def. below).
One finds that (co-)modalities are a fully equivalent perspective on the (co-)reflective subcategories of their fully (co-)modal objects (Def. below), this is the statement of Prop. below.
Another alternative perspective on this situation is given by the concept of localization of categories (Def. below), which is about universally forcing a given collection of morphisms (“weak equivalences”, Def. below) to become invertible. A reflective localization is equivalently a reflective subcategory-inclusion (Prop. below), and this exhibits the modal objects (Def. below) as equivalently forming the full subcategory of local objects (Def. below).
Conversely, every reflection onto full subcategories of -local objects (Def. below) satisfies the universal property of a localization at with respect to left adjoint functors (Prop. below).
In conclusion, we have the following three equivalent perspectives on modalities.
| reflective subcategory | modal operator | reflective localization |
|---|---|---|
| object in reflective full subcategory | modal object | local object |
Definition
(reflective subcategory and coreflective subcategory)
Let be a category (Def. ) and
a full subcategory-inclusion (hence a fully faithful functor Def. ). This is called:
-
a reflective subcategory inclusion if the inclusion functor has a left adjoint def. )
then called the reflector;
-
a coreflective subcategory-inclusion if the inclusion functor has a right adjoint (def. )
then called the coreflector.
Example
(reflective subcategory inclusion of sets into small groupoids)
There is a reflective subcategory-inclusion (Def. )
of the category of sets (Example ) into the category Grpd (Example ) of small groupoids (Example ) where
-
the right adjoint full subcategory inclusion (Def. ) sends a set to the groupoid with set of objects being , and the only morphisms being the identity morphisms on these objects (also called the discrete groupoid on , but this terminology is ambiguous)
-
the left adjoint reflector sends a small groupoid to its set of connected components, namely to the set of equivalence classes under the equivalence relation on the set of objects, which regards two objects as equivalent, if there is any morphism between them.
We now re-consider the concept of reflective subcategories from the point of view of modalities:
Definition
(modality)
Let be a category (Def. ). Then
-
a modal operator on is
-
an endofunctor
whose full essential image we denote by
-
a natural transformation (Def. )
(23)for all objects , to be called the unit morphism;
such that:
-
for every object in the essential image of , every morphism into factors uniquely through the unit (23)
which equivalently means that if the operation of precomposition with the unit yields a bijection of hom-sets
(24)
-
-
a comodal operator on is
-
an endofunctor
whose full essential image we denote by
-
a natural transformation (Def. )
(25)for all objects , to be called the counit morphism;
such that:
-
for every object in the essential image of , every morphism out of factors uniquely through the counit (23)
which equivalently means that if the operation of postcomposition with the counit yields a bijection of hom-sets
(26)
-
Proposition
(modal operators equivalent to reflective subcategories)
If
is a reflective subcategory-inclusion (Def. ). Then the composite
equipped with the adjunction unit natural transformation (Def. )
is a modal operator on (Def. ).
Dually, if
is a coreflective subcategory-inclusion (Def. ). Then the composite
equipped with the adjunction counit natural transformation (Def. )
is a comodal operator on (Def. ).
Conversely:
If an endofunctor with natural transformation is a modal operator on a category (Def. ), then the inclusion of its full essential image is a reflective subcategory inclusion (Def. ) with reflector given by the corestriction of to its image:
Dually, if an endofunctor with natural transformation is a comodal operator (Def. ), then the inclusion of its full essential image is a coreflective subcategory inclusion (Def. ) with coreflector given by the corestriction of to its image
Proof
The first two statements are immedialy a special case of the characterization of adjunctions via universal morphisms in Prop. : Using that is here assumed to be fully faithful, the uniqueness of in the universal morphism-factorization condition (21)
implies that also is the unique morphism making that triangle commute.
Similarly for the converse: The assumption on a modal operator is just so as to make its unit be a universal morphism (Def. ) into the inclusion functor of its essential image.
Proposition
(modal operator is idempotent)
Let be a category (Def. ).
For a modal operator on , with unit (Def. ), it is idempotent, in that it is naturally isomorphic (Def. ) to the composition with itself:
In fact, the image under of its unit is such an isomorphism
as is its unit on its image
Formally dually, for a comodal operator on , with counit (Def. ), it is idempotent, in that it is naturally isomorphic (Def. ) to the composition with itsef:
In fact, the image under of its counit is such an isomorphism
as is its counit on its image
Proof
We discuss the first case, the second is formally dual (Example ).
By Prop. , the modal operator is equivalent to the composite obtained from the reflective subcategory-inclusion (Def. ) of its essential image of modal objects:
and its unit is the corresponding adjunction unit (Def. )
Hence it is sufficient to show that the morphisms and and are isomorphisms.
Now, the triangle identities (18) for the adjunction , which hold by Prop. , say that their composition with the adjunction counit is the identity morphism
But by Prop. , the counit is a natural isomorphism, since is fully faithful. Hence we may cancel it on both sides of the triangle identities and find that and are indeed isomorphisms.
Definition
Let be a category (Def. ).
For a modal operator on (Def. ), we say:
-
a -modal object is an object such that the following conditions hold (which are all equivalent, by Prop. ):
-
it is in the -essential image: ,
-
it is isomorphic to its own -image: ,
-
specifically its -unit is an isomorphism .
-
-
a -submodal object is an object , such that
- its -unit is a monomorphism (Def. ): .
Dually (Example ):
For a comodal operator on (Def. ), we say:
-
a -comodal object is an object such that the following conditions hold (which are all equivalent, by Prop. ):
-
it is in the -essential image: ,
-
it is isomorphic to its own -image: ,
-
specifically its -counit is an isomorphism
-
-
a -supcomodal object is an object , such that
- its -counit is an epimorphism (Def. ): .
Definition
Let
be an adjoint triple (Remark ) such that and are fully faithful functors (necessarily both, by Prop. ). By Prop. , there are induced modal operators
which themselves form am adjoint pair
hence called an adjoint modality. The adjunction unit and adjunction counit as in (13) may now be read as exhibiting each object in the domain of as “in between the opposite extremes of its -modal aspect and its -modal aspect”
A formally dual situation (Example ) arises when is fully faithful.
with
and canonical natural transformation between opposite extreme aspects given by
Proposition
(fully faithful adjoint triple)
Let be an adjoint triple (Remark ). Then the following are equivalent:
-
is a fully faithful functor;
-
is a fully faithful functor,
-
is an adjoint modality (Def. ).
For proof see this prop..
In order to analyze (in Prop. below) the comparison morphism of opposite extreme aspects (27) induced by an adjoint modality (Def. ), we need the following technical Lemma:
Lemma
Let
be an adjoint triple with induced adjoint modality (Def. ) to be denoted
Denoting the adjunction units/counits (Def. ) as
| adjunction | unit | counit |
|---|---|---|
we have that the following composites of unit/counit components are equal:
Proof
We claim that the following diagram commutes (Def. ):
This commutes, because:
-
the left square is the image under of naturality (4) for on ;
-
the top square is naturality (4) for on ;
-
the right square is naturality (4) for on ;
-
the bottom commuting triangle is the image under of the triangle identity (18) for on .
Moreover, notice that
-
the total bottom composite is the identity morphism , due to the triangle identity (18) for ;
-
also the other two morphisms in the bottom triangle are isomorphisms, as shown, due to the idempoency of the -adjunction (Prop. .)
Therefore the total composite from along the bottom part of the diagram equals the left hand side of (28), while the composite along the top part of the diagram clearly equals the right hand side of (28).
Proposition
(comparison transformation between opposite extremes of adjoint modality)
Consider an adjoint triple of the form
with induced adjoint modality (Def. ) to be denoted
Denoting the adjunction units/counits (Def. ) as
| adjunction | unit | counit |
|---|---|---|
Then for all the following two natural transformations, constructed from the adjunction units/counits (Def. ) and their inverse morphisms (using idempotency, Prop. ), are equal:
Moreover, the image of these morphisms under equals the following composite:
hence
Proof
The first statement follows directly from Lemma .
For the second statement, notice that the -adjunct (Prop. ) of
is
where under the braces we uses the triangle identity (Prop. ).
(As a side remark, for later usage, we observe that the morphisms on the left in (32) are isomorphisms, as shown, by idempotency of the adjunctions.)
From this we obtain the following commuting diagram:
Here:
-
on the left we identified by applying the formula (Prop. ) for -adjuncts to (32);
-
on the right we used the triangle identity (Prop. ) for .
This proves the second statement.
Definition
(preorder on modalities)
Let and be two modal operators on a category . By Prop. these are equivalently characterized by their reflective full subcategories of modal objects.
There is an evident preorder on full subcategories of , given by full inclusions of full subcategories into each other. We write if the full subcategory on the left is contained, as a full subcategory of , in that on the right. Via prop. there is the induced preorder on modal operators, and we write
There is an analogous preorder on comodal operators (Def. ).
If we have two adjoint modalities (Def. ) of the same type (both modal left adjoint or both comodal left adjoint) such that both the modalities and the comodalities are compatibly ordered in this way, we denote this situation as follows:
etc.
Example
(bottom and top adjoint modality)
Let be a category with both an initial object and a terminal object (Def. ). Then, by Example there is an adjoint triple between and the terminal category (Example ) of the form
The induced adjoint modality (Def. ) is
By slight abuse of notation, we will also write this as
On the other extreme, for any category whatsoever, the identity functor on it is adjoint functor to itself, and constitutes an adjoint modality (Def. )
Here
in the preorder on adjoint modalities according to Def. , in that for every adjoint modality of the form we have the following:
Definition
On some category , consider an inclusion of adjoint modalities, according to Def. :
We say:
Remark
For a progression of adjoint modalities of the form
the analog of Aufhebung (Def. ) is automatic, since, by Prop. , in this situation the full subcategories modal objects at each stage coincide already.
For emphasis we may denote this situation by
Example
(top adjoint modality provides Aufhebung of all oppositions)
For any category, the top adjoint modality (Def. ) provides Aufhebung (Def. ) of every other adjoint modality.
But already Aufhebung of the bottom adjoint modality is a non-trivial and interesting condition. We consider this below in Prop. .
We now re-consider the concept of reflective subcategories from the point of view of localization of categories:
Definition
(category with weak equivalences)
A category with weak equivalences is
-
a category (Def. )
-
a subcategory (i.e. sub-class of objects and morphisms that inherits the structure of a category)
such that the morphisms in
-
include all the isomorphisms of ,
-
satisfy two-out-of-three:
If for , any two composable morphisms in , two out of the set are in , then so is the third.
Definition
Let be a category with weak equivalences (Def. ). Then the localization of at is, if it exsists
such that
-
sends all morphisms in to isomorphisms (Def. ),
-
is universal with this property: If is any functor with this property, then it factors through , up to natural isomorphism (Def. ):
and any two such factorizations and are related by a unique natural isomorphism compatible with and :
Such a localization is called a reflective localization if the localization functor has a fully faithful right adjoint, exhibiting it as the reflection functor of a reflective subcategory-inclusion (Def. )
Proposition
(reflective subcategories are localizations)
Every reflective subcategory-inclusion (Def. )
is the reflective localization (Def. ) at the class of morphisms that are sent to isomorphisms by the reflector .
Proof
Let be a functor which inverts morphisms that are inverted by .
First we need to show that it factors through , up to natural isomorphism. But consider the following whiskering of the adjunction unit (Def. ) with :
By idempotency (Prop. ), the components of the adjunction unit are inverted by , and hence by assumption they are also inverted by , so that on the right the natural transformation is indeed a natural isomorphism.
It remains to show that this factorization is unique up to unique natural isomorphism. So consider any other factorization via a natural isomorphism . Pasting this now with the adjunction counit
exhibits a natural isomorphism between . Moreover, this is compatible with according to (35), due to the triangle identity (Prop. ):
Finally, since is essentially surjective functor, by idempotency (Prop. ), it is clear that this is the unique such natural isomorphism.
Definition
Let be a category (Def. ) and let be a set of morphisms. Then an object is called an -local object if for all the hom-functor (Def. ) from into yields a bijection
hence if every morphism extends uniquely along to :
We write
for the full subcategory (Example ) of -local objects.
Definition
(reflection onto full subcategory of local objects)
Let be a category and set be a sub-class of its morphisms. Then the reflection onto local -objects (often just called “localization at the collection ” is, if it exists, a left adjoint (Def. ) to the full subcategory-inclusion of the -local objects (36):
A class of examples is the following, which comes to its full nature (only) after passage to homotopy theory (Example below):
Definition
(homotopy localization of 1-categories)
Let be a category, let be an object, and consider the class of morphisms given by projection out of the Cartesian product with , of all objects :
If the corresponding reflection onto the full subcategory of local objects (Def. ) exists, we say this is homotopy localization at that object , and denote the modal operator corresponding to this (via Prop. ) by
Proposition
(reflective localization reflects onto full subcategory of local objects)
Let be a category with weak equivalences (Def. ). If its reflective localization (Def. ) exists
then is equivalently the inclusion of the full subcategory (Example ) on the -local objects (Def. ), and hence is equivalently reflection onto the -local objects, according to Def. .
Proof
We need to show that
-
every is -local,
-
every is -local precisely if it is isomorphic to an object in .
The first statement follows directly with the adjunction isomorphism (10):
and the fact that the hom-functor takes isomorphisms to bijections (Example ).
For the second statement, consider the case that is -local. Observe that then is also local with respect to the class
of all morphisms that are inverted by (the “saturated class of morphisms”): For consider the hom-functor to the opposite of the category of sets. By assumption on this takes elements in to isomorphisms. Hence, by the defining universal property of the localization-functor , it factors through , up to natural isomorphism.
Since, by idempotency (Prop. ), the adjunction unit is in , this implies that we have a bijection of the form
In particular the identity morphism has a preimage under this function, hence a left inverse to :
But by 2-out-of-3 this implies that . Since the first item above shows that is -local, this allows to apply this same kind of argument again,
to deduce that also has a left inverse . But since a left inverse that itself has a left inverse is in fact an inverse morphisms (this Lemma), this means that is an inverse morphism to , hence that is an isomorphism and hence that is isomorphic to an object in .
Conversely, if there is an isomorphism from to a morphism in the image of hence, by the first item, to a -local object, it follows immediatly that also is -local, since the hom-functor takes isomorphisms to bijections and since bijections satisfy 2-out-of-3.
Proposition
(reflection onto local objects is localization with respect to left adjoints)
Let be a category (Def. ) and let be a class of morphisms in . Then the reflection onto the -local objects (Def. ) satisfies, if it exists, the universal property of a localization of categories (Def. ) with respect to left adjoint functors inverting .
Proof
Write
for the reflective subcategory-inclusion of the -local objects.
Say that a morphism in is an -local morphism if for every -local object the hom-functor (Example ) from to yields a bijection . Notice that, by the Yoneda embedding for (Prop. ), the -local morphisms are precisely the morphisms that are taken to isomorphisms by the reflector (via Example ).
Now let
be a pair of adjoint functors, such that the left adjoint inverts the morphisms in . By the adjunction hom-isomorphism (10) it follows that takes values in -local objects. This in turn implies, now via the Yoneda embedding for , that inverts all -local morphisms, and hence all morphisms that are inverted by .
Thus the essentially unique factorization of through now follows by Prop. .
Last revised on June 11, 2024 at 17:29:10. See the history of this page for a list of all contributions to it.